Министерство образования Республики Беларусь
Учреждение образования
"Гомельский государственный университет им. Ф. Скорины"
Математический факультет
Кафедра МПМ
Методика изучения функций в школьном курсе математики
Реферат
Исполнитель:
Студентка группы М-33 Грабовец А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Лебедева М.Т.
Гомель 2007
Содержание
Введение
1. Различные подходы к трактовке понятия функции в курсе математики в средней школе
2. Основные направления введения понятия функции в школьном курсе математики
3. Методика формирования понятий общих свойств функций
4. Методическая схема изучения функций. Изучение функций в классе функций
Заключение
Литература
Функциональная линия школьного курса математики – одна из ведущих, определяющая стиль изучения тем в курсах алгебры и начала анализа. Её особенность состоит в представлении возможности установления разнообразных связей в обучении.
В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе функциональной линии в системе обучения строится так, чтобы внимание учащихся сосредотачивалось на:
1) выделенных и достаточно четко разграниченных представлениях, связанных с функцией;
2) установлении их взаимодействия при развёртывании учебного материала.
Задача. При каких значениях параметра а уравнение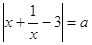 
имеет ровно четыре корня?
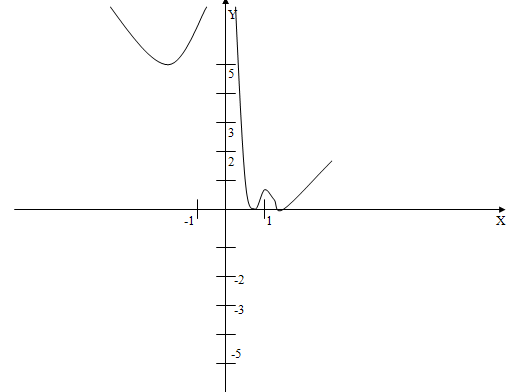
Строим графики функци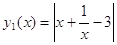й 
и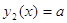 
в одной системе координат, воспринимая равенство как равенство значений выбранных функций.
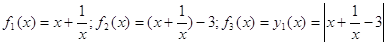
Построим график 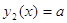четыре точки пересечения получаем для $IMAGE7$. При $IMAGE8$ (координаты точки максимума (1,2)) получаем верхнее ограничение. Второй промежуток значений для $IMAGE9$: от точки минимума функции, т.е. $IMAGE10$. Основа решения – использование функциональных и графических представлений, а само решение – переход от исследования данного в уравнении к исследованию функции. При построении графика этой функции $IMAGE11$ с помощью элементарных преобразований графиков наиболее трудным является оценивание значения выражения $IMAGE12$. В качестве подсказки можно воспользоваться неравенством:
$IMAGE13$
Показанный метод называется функционально-графическим моделированием. Освоение его и с формальной, и с прикладной стороны в значительной мере подчинено изучение всей функциональной линии курсов алгебры и начала анализа.
Различают две основные математические трактовки понятия функции:
1) генетическую;
2) логическую.
Основные понятия, используемые при генетической трактовке: переменная величина, функциональная зависимость переменных величин, формула (выражающая одну переменную через некоторую комбинацию других переменных), декартова система координат на плоскости. Достоинство такого подхода состоит в том, подчеркивая динамический характер понятия функциональной зависимости, выявляется модельный аспект понятия функции относительно изучения явлений природы. Например, общая схема применения функции для описания результатов опыта имеет вид:
1)провести эксперимент;
2)составить по результатам эксперимента таблицу значений связанных друг с другом величин;
3)построить по табличным данным график;
4)подобрать эмпирическим путём формулу для данной функции;
5)дать развёрнутую характеристику свойств функции;
6)истолковать установленные свойства функции на языке эксперимента.
Однако ограничительная черта в этом подходе в том, что переменная всегда неявно предполагается пробегающей непрерывный ряд числовых значений. Поэтому понятие связывается с числовыми функциями числовог8о аргумента.
Логическая трактовка: обучение функциональным представлениям следует строить на основе методического анализа понятия функции в поисках понятия алгебраической системы. Здесь функция – отношение специального вида между двумя множествами, удовлетворяющее условие функциональности. Начальный этап изучения – понятие отношения. Реализация логического подхода вызывает необходимость иллюстрировать понятие функции при помощи разнообразных средств: формулы, таблицы, задание функции стрелками, перечислением пар, использованием не только числового, но и геометрического материала(теперь и геометрическое преобразование можно рассматривать как функцию). Однако наработанные таким образом общие понятия в дальнейшем связываются только с числовыми функциями одного числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия.
В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе функциональной линии в системе обучения строится так, чтобы внимание учащихся сосредотачивалось на:
1) выделенных и достаточно четко разграниченных представлениях, связанных с функцией;
2) установлении их взаимодействия при развёртывании учебного материала.
Выделена система компонентов и установлена связь между ними. В систему входят такие компоненты: 1) представление о функциональной зависимости переменных величин в реальных процессах и математике; 2) представление о функции как о соответствии;3) построение и использование графиков функций, использование графиков функций; 4) вычисление значений функций, определённых различными способами;
Введение понятия ведётся по трём основным направлениям: 1) упорядочение основных представлений о функции; развёртывание системы понятий, характерных для функциональных линий (способы задания и общие свойства функций, графическое истолкование области определения, области значения, возрастания и т. д. на основе метода координат); 2) глубокое изучение отдельных функций и их классов; 3) расширения области приложения алгебры за счёт включения в нею идеи функции и разветвлённой системы действий с функцией.
Первое направление появляется в алгебре ранее остальных. Основной акцент – усвоение учащимися однозначности соответствия аргумента и определяемого по нему значения функции. Из разнообразных способов задания функции чаще всего используется способ задания функции формулой остальные способы задания – подчинённые. Сопоставление различных способов задания вызвано практической потребностью и важно для усвоения всего многообразия понятия функции.
Использование перевода задания функции из одной формы представления в другую – необходимый методический приём приведении понятия функции. Реализация – система заданий, в которых представлены все случаи такого перевода. Например, при отработке формы представления можно рассмотреть задачи:
1. изобразить график функции у=4х+1 на $IMAGE14$ ;
2. проверить, на сколько точна таблица квадратов чисел, взяв несколько значений для аргумента проведя расчёт : х=1.35; 2.44; 9,4; 7; 6,25;
3. по заданным точкам построить график зависимости.
В первом задании построение идёт по точкам, так как первоначально учащиеся не знают вида графика линейной функции. Способ построения графика функции по точкам иллюстрирует задание три, второе задание иллюстрирует связь функциональных представлений с числовой системой. Второй тип заданий – оптимизация представления функции без изменения средств представлений. Типичные задания: упростить формулу, задающую функцию. Цель таких задания – показать, что одна и та же функция может определяться различными формулами. Связь функциональной линии с числовой системой при введении понятия функции осуществляется при вычислении её значения по формуле или словесному описанию. Учащиеся должны понимать, что если о некоторой функции известно, что она определена на множестве $IMAGE15$, то это значит, что для каждого $IMAGE16$ можно найти соответствующее значение $IMAGE17$.
Например: Функция задана формулой : $IMAGE18$. Найти её значение при $IMAGE19$. Наряду с раскрытием определения понятия уточнения общих функциональных представлений введение понятия функции требует рассмотрения нескольких конкретных примеров функций.
В школьной математике функции образуют классы, обладающие общностью аналитического способа задания, сходными особенностями графиков, областей применения. В курсе алгебры происходит вживление основных понятий функциональной линии. Каждая функция представлена в виде объекта, и её освоение происходит в сопоставлении черт, специфических для неё. Переходя к изучению класса функций (например, линейных) необходимо исследовать данную функцию, как член класса и изучить свойства всего класса на примере типичной функции.
Связи внутри функциональной линии при изучении функций:
1). Индивидуально-заданная функция
Общее понятие функции $IMAGE20$ данная функция $IMAGE20$ характерные приёмы изучения и исследования данной функции
2). Функция, входящая в класс
Общее понятии функции $IMAGE20$ данная функция $IMAGE20$ общие свойства класса функций $IMAGE24$характерные приёмы изучения и исследования функций данного класса $IMAGE24$ведущие примеры функций данного класса.
Методика изучения общих функциональных понятий.
Понятие функции вводится в 7 классе, многие общие функциональные понятия вводятся в теме "Числовые функции" в 4 классе. Только понятие периодичности вводится в 10 классе и в 11 – понятие функции, обратной данной.
Методическая схема введения понятия функции:
1. Понятие функции вводится конкретно-индуктивным способом;
2. На основании конкретной формулы устанавливаются характеристические свойства общего понятия функции: области определения, значения, зависимость: каждому $IMAGE26$ - единственное значение $IMAGE27$.
3. Формулируются определения функции, сообщается учителем область определения и область значения.
4. Проиллюстрировать сказанное рисунком.
5. Привести контр пример понятия функции: $IMAGE28$; область определения $IMAGE29$; область значений $IMAGE30$.
6. Рассмотреть упражнения.
7. Закрепить формулировку понятия функции.
По этой же схеме можно изучать и остальные общие функциональные свойства: чётность, монотонность, периодичность и т.д.
Методические схема изучения функции.
1. Рассмотреть подводящую задачу, с помощью которой мотивируется изучение новой функции.
2. На основе математизации эмпирического материала сформулировать определение функции (сообщить формулу).
3. Составить таблицу значений функции и построить "по точкам" её график.
4. Провести исследование основных свойств функции (преимущественно по графику)
5. Рассмотреть задачи и упражнения на применение изученных свойств функции.
Особенность схемы-исследования функции имеет наглядно-геометрический подход, аналитическое исследование имеет ограниченный характер. Схема применима в изучении линейной, квадратичной, степенной и других функций, с которыми учащиеся знакомятся в курсе алгебры.
Изучение функций в классе функций. Класс линейных функций.
Типичный для математики класс функций – линейные. Первоначальное представление связывается с равномерным прямолинейным движением или с построением графика некоторой линейной функции. Рассматривая второй источник можно убедиться в том, что график отдельно взятой линейной функции не может привести к формулированию представлений об основных свойствах графиков всех линейных функций.
Первый способ: использование загущения точек на графике. а) нанесение нескольких точек; б) наблюдение – все построенные точки расположены на одной прямой; в) проверка – берём произвольное значение аргумента и вычисляем по нему значения функции; г) наносим точку на координатную плоскость – она принадлежит построенной прямой. Такой приём приведёт к пониманию того, что график любой линейной функции – прямая (выделение одного из свойств линейной функции), на его проведение потребует очень много времени и общие свойства формулируется на изолированных примерах.
Второй способ: по двум точкам. Этот способ предполагает знание соответствующего свойства графиков линейных функций, выявление новых свойств не происходит.
При обучении происходит последовательная схема этих способов.
Для изучения класса линейных функций в совокупности его общих свойств перед учащимися ставится познавательная задача исследовать класс функций $IMAGE31$ в зависимости от параметров, здесь лучше всего рассмотреть несколько функций с различными параметрами,
Например: Постройте графики функций $IMAGE32$у=0.5х; у=0.5х+ 0.5; у=1.5х; у=1.5х+0.5.
Дальше необходимо их сравнить, обращая внимание на особенности, связанные с числовыми значением коэффициентов.
Например, изучая геометрический смысл коэффициентов при переменной, отличаем одинаковость углов наклонов к оси $IMAGE33$, чем меньше этот коэффициент, тем меньший угол нак