Знакочередующиеся и знакопеременные ряды
Содержание
1. Признак Даламбера
2. Признак Коши
3. Интегральный признак сходимости ряда
4. Знакочередующиеся ряды. Признак Лейбница
5. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды
Список использованных источников
1. Признак Даламбера
Теорема 1 (признак Даламбера). Пусть дан ряд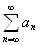 
, где все 
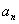> 0. 
Если существует предел
,
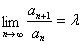то при 0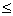 
$IMAGE6$<1 ряд сходится, а при $IMAGE6$ > 1 ряд сходится.
◄Пусть существует предел
$IMAGE8$,
где 0 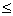$IMAGE6$<1. Возьмем q такое, что $IMAGE6$< q <1. Тогда для любого числа ε > 0, например, для
$IMAGE12$,найдется номер N такой, что для всех n ≥ N будет выполняться неравенство
$IMAGE13$ < q - $IMAGE6$,
В частности, будем иметь
$IMAGE15$ < q - $IMAGE6$,
или
$IMAGE17$ < q,
Откуда $IMAGE18$ < 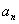q для всех n ≥ N. Из этого неравенства, придавая n последовательно значения N, N+1,N+2, получим
$IMAGE20$ < $IMAGE21$q,
$IMAGE22$ < $IMAGE20$q < $IMAGE21$q $IMAGE25$,
$IMAGE26$ < $IMAGE22$q < $IMAGE21$q $IMAGE29$,
………………………….
Члены ряда
$IMAGE20$+ $IMAGE22$+ $IMAGE26$+…
Не превосходят соответствующих членов ряда
$IMAGE21$q + $IMAGE21$q + $IMAGE21$q $IMAGE29$+… ,
который сходятся как ряд, составленный из членов геометрической прогрессии со знаменателем q ,0 < q < 1. По признаку сравнения ряд
$IMAGE20$+ $IMAGE22$+ $IMAGE26$+…
сходится, а значит, сходится и исходный ряд $IMAGE40$.
В случае $IMAGE6$ > 1, начиная с некоторого номера N, будет выполняться неравенство
$IMAGE42$ > 1, или $IMAGE20$ > $IMAGE21$ > 0.
Следовательно, $IMAGE45$ 0, и ряд $IMAGE46$ расходится, так как не выполнен необходимый признак сходимости. ►
Замечание. Если
$IMAGE47$1,
Или не существует, то признак Даламбера ответа о сходимости или расходимости ряда не дает.
Примеры. Исследовать на сходимость следующие ряды:
1. $IMAGE48$ .
◄ Для данного ряда имеем
$IMAGE49$, $IMAGE50$.
Тогда
$IMAGE47$ $IMAGE52$ $IMAGE53$.
По признаку Даламбера ряд сходится. ►
2. $IMAGE54$ .
◄ Имеем
$IMAGE55$, $IMAGE56$= $IMAGE57$;
$IMAGE47$ $IMAGE59$ $IMAGE60$.
Данный ряд расходится. ►
2. Признак Коши
Теорема 2 (признак Коши). Пусть дан ряд
$IMAGE40$, $IMAGE62$ . (1)
Если существует конечный предел
$IMAGE63$,
то 1) при $IMAGE64$ ряд сходится;2) при $IMAGE65$ ряд расходится.
◄ 1) Пусть $IMAGE66$. Возьмем число q такое, что $IMAGE67$. Так как существует предел
$IMAGE63$,
где $IMAGE70$, то, начиная с некоторого номера N , будет выполняться неравенство $IMAGE71$.
В самом деле, из определенного равенства вытекает, что для любого ε ,в том числе и для
ε = $IMAGE72$, найдется такой номер N , начиная с которого будет выполняться неравенство
$IMAGE73$,
откуда $IMAGE74$ $IMAGE75$ $IMAGE76$ или что тоже,
$IMAGE71$.
Отсюда получаем
$IMAGE78$ для $IMAGE79$.
Таким образом, все члены ряда, начиная с $IMAGE20$, меньше соответствующих членов сходящегося ряда $IMAGE81$. По признаку сравнения ряд
$IMAGE82$
сходится, а значит сходится и ряд(1).
2)Пусть $IMAGE84$. Тогда, начиная с некоторого номера N для всех n > N , будет выполняться неравенство $IMAGE85$, или
$IMAGE86$.
Следовательно,
$IMAGE87$
И ряд (1) расходится. ►
Замечание. Если $IMAGE88$, то ряд (1) может как сходиться, так и расходиться.
Примеры. Исследовать на сходимость следующие ряды:
1. $IMAGE89$ .
◄ Имеем
$IMAGE90$, $IMAGE91$;
$IMAGE92$ $IMAGE93$.
Ряд сходится. ►
2. $IMAGE94$
◄ Здесь
$IMAGE95$, $IMAGE96$;
$IMAGE92$ $IMAGE98$
Ряд сходится. ►
3. Интегральный признак сходимости ряда
Теорема 3 (интегральный признак сходимости). Пусть функция f(x) определена, непрерывна, положительна и не возрастает на луче $IMAGE99$. Тогда:
1) числовой ряд $IMAGE100$ сходится, если сходится несобственный интеграл
$IMAGE101$ ; (1)
2) ряд $IMAGE100$ расходится, если расходится несобственный интеграл (1)
$IMAGE103$
◄ Возьмем на графике функции f(x) точки с абсциссами
x1=1, x2=2, x3=3, … , xn = n
и построим две ступенчатые фигуры, состоящие из выступающих и входящих прямоугольников так, как показано рис. 1. Площадь Q криволинейной трапеции, ограниченной прямыми x = 1, x = n, y=0 и кривой y = f(x) равна
$IMAGE104$.
Возьмем n-ю частичную сумму ряда $IMAGE100$:
S n = f(1) + f(2) + f(3) + … + f(n) ,
Тогда площадь Q+ выступающей фигуры будет равна
Q+= f(1) + f(2) + f(3) + … + f(n-1) = S n-1
А площадь Q- входящей фигуры равна
Q- = + f(2) + f(3) + … + f(n) = S n - f(1).
Из построения и свойств функции f(x) следует, что
Q- < Q < Q+ , т.е.
S n - f(1) < $IMAGE106$< S n-1.
Так как S n-1 < S n (в силу условия $IMAGE107$), то
S n - f(1) < $IMAGE106$< S n, n =1,2, … . (2)
1) Пусть интеграл (1) сходится. Тогда существует предел
$IMAGE109$,
так как
$IMAGE110$ $IMAGE101$
(в силу условия f(x) > 0 для $IMAGE112$ , то из неравенства (2) следует, что
S n < f(1) + $IMAGE106$≤ f(1) + A = M = const,
т.е. 0 < S n < M для n = 1, 2, … .Тем самым, последовательность {S n} ограничена, и при возрастании n сумма S n возрастает, так как f(n ) > 0 для n = 1, 2, … . Поэтому она имеет предел
$IMAGE114$,
Что означает сходимость ряда $IMAGE100$.
2) Пусть интеграл (1) расходится. Так как по условию
f(x) > 0 для $IMAGE99$, то
$IMAGE101$= $IMAGE118$.
Из неравенства
S n ≥ $IMAGE106$, n = 1, 2, … ,
Следует, что
$IMAGE120$,
т.е. ряд $IMAGE100$ расходится. ►
Пример 1. Исследовать на сходимость ряд
$IMAGE122$.
◄ Здесь $IMAGE123$. Известно, что несобственный интеграл
$IMAGE124$
сходится при p > 1 и расходится при p ≤ 1. Следовательно, данный ряд сходится при p > 1 и расходится
при p ≤ 1. В частности, при p = 1 получим гармонический ряд
$IMAGE125$►
Пример 2. Исследовать на сходимость ряд
$IMAGE126$.
◄ В данном случае функция $IMAGE127$ и
$IMAGE128$= $IMAGE129$= $IMAGE130$ $IMAGE131$=
= $IMAGE132$(arctg b-arctg 1)= $IMAGE133$,
т.е. интеграл
$IMAGE128$
сходится, а значит, сходится и ряд. ►
Пример 3. Исследовать на сходимость ряд
$IMAGE135$
◄ Так как общий член данного ряда имеет вид $IMAGE136$, то выбираем функцию $IMAGE137$.
Несобственный интеграл
$IMAGE138$= $IMAGE139$= $IMAGE140$=
= $IMAGE141$= + $IMAGE142$
расходится, следовательно, ряд тоже расходится. ►
Замечание. Нижний предел интегрирования в несобственном интеграле
$IMAGE101$
можно взять произвольным, например, равным а, где а ≥ 1 – любое число.
Пример 4. Исследовать сходимость ряда
$IMAGE144$,
◄ Так как общий член ряда
$IMAGE145$
то в качестве функции $IMAGE146$ возьмем
$IMAGE147$, где x ≥ 4.
Тогда
$IMAGE148$= $IMAGE149$=
= $IMAGE150$= $IMAGE151$
= $IMAGE152$ $IMAGE153$.
Так как несобственный интеграл
$IMAGE148$
сходится, то сходится и исходный ряд. ►
В случае сходимости ряда $IMAGE100$ метод, примененный при доказательстве интегрального признака сходимости, позволяет получить оценку погрешности, возникающей при замене суммы ряда частичной суммой.
Пусть функция f(x) удовлетворяет условиям теоремы 9, ряд
$IMAGE100$
сходится и его сумма равна S. Можно показать, что в этом случае будет сходиться и несобственный интеграл
$IMAGE101$.
Пользуясь неравенством
$IMAGE158$,
оценим остаток Rn заданного ряда, Имеем
$IMAGE159$.
Итак,
$IMAGE160$
Таким образом, погрешность, получаемая при замене суммы S сходящегося ряда $IMAGE100$
его n-й частичной суммой Sn , не превосходит интеграла $IMAGE162$.
Пример 5. Установить сходимость ряда
$IMAGE163$
и оценить погрешность при замене его суммы S5.
◄ Здесь
$IMAGE164$= $IMAGE165$= $IMAGE166$= = $IMAGE167$= $IMAGE168$
В силу интегрального признака ряд сходится. Обозначим сумму этого ряда через S и будем считать, что
S ≈ S5. Тогда
S ≈ S5 == $IMAGE169$
$IMAGE170$
Оценим погрешность R5. Имеем
$IMAGE171$ $IMAGE172$ ►
Замечание. Обозначение
$IMAGE173$
понимается так
$IMAGE173$= $IMAGE175$= $IMAGE176$ $IMAGE177$=
= $IMAGE178$.
Пример 6. Оценить n-й остаток сходящегося ряда
$IMAGE179$
где p>1.
◄ Имеем
$IMAGE180$ = $IMAGE181$ = $IMAGE182$= $IMAGE183$. ►
4 Знакочередующиеся ряды. Признак Лейбница
Определение. Числовой ряд
a1 – a2 + a3 – … + (– 1) n - 1an + … ,
где все числа an положительны, называется знакочередующимся.
Пример. Ряд
$IMAGE184$
является знакочередующимся, а ряд
$IMAGE185$
знакочередующимся не является.
Для знакочередующихся рядов имеет место следующий признак сходимости, который носит название признака Лейбница.
Теорема 4 (признак Лейбница). Пусть в знакочередующемся ряде
a1 – a2 + a3 – …
числовая последовательность { an } убывает,
a1 > a2> a3> … $IMAGE186$ Тогда этот ряд сходится, причем его сумма S положительна и не превосходит первого члена:
$IMAGE187$
◄ Возьмем четную частичную сумму S2n этого ряда и запишем ее в виде
S2n = (a1 – a2) + (a3 – a4) + … + (a2n-1 – a2n).
Из условия теоремы следует, что разности в скобках положительны и, значит, S2n > 0,
причем с возрастанием n частичная сумма S2n возрастает. Эту сумму можно записать
и так:
S2n = a1 – (a2 – a3) – (a4 – a5) – … – (a2n-2 – a2n-1) – a2n.
Здесь каждая скобка положительна, откуда следует, что
S2n < a1 (n = 1, 2, … ).
Итак, последовательность { S2n } монотонно возрастает и ограничена. Следовательно,
она имеет предел
$IMAGE188$,
причем $IMAGE187$
Для нечетной частичной суммы S2n+1 будем иметь
S2n+1 = S2n + a2n+1 (n = 1, 2, … ).
По доказанному
$IMAGE188$,
А по условию теоремы
$IMAGE191$
Поэтому существует предел
$IMAGE192$ $IMAGE193$ $IMAGE194$.
Таким образом, доказано, что
$IMAGE195$,
т.е. данный ряд сходится. Из неравенства $IMAGE196$ следует, в частности, положительность суммы ряда. ►
Замечание. Теорема остается справедливой в части сходимости, если условие монотонности последовательности { an } будет выполняться для всех номеров n, начиная с некоторого номера N.
Пример. Знакочередующийся ряд
$IMAGE197$
сходится, так как
$IMAGE198$ и $IMAGE199$
Теорема 4 позволяет оценить n-й остаток
$IMAGE200$
Рассматриваемого ряда, который также является знакочередующимся рядом. По абсолютной величине остаток будет не больше абсолютной величины первого своего члена, $IMAGE201$. Так как $IMAGE202$, то
$IMAGE203$
т.е абсолютная погрешность