Застосування подвійних інтегралів
Содержание
1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах
2. Застосування подвійних інтегралів до задач геометрії
3. Застосування подвійних інтегралів до задач механіки
1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах Нехай функція 
неперервна в деякій замкненій і обмеженій області 
, тоді існує інтеграл
.
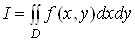Припустимо, що за допомогою формул
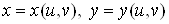(1)
ми переходимо в інтегралі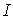 
до нових змінних $IMAGE6$ та $IMAGE7$. Вважатимемо, що з формул (1) однозначно можна визначити $IMAGE6$ та $IMAGE7$:
$IMAGE10$. (2)
Згідно з формулами (2), кожній точці $IMAGE11$ ставиться у відповідність деяка точка $IMAGE12$ на координатній площині з прямокутними координатами $IMAGE6$ і $IMAGE7$.
Нехай множина всіх точок $IMAGE12$ утворює обмежену замкнену область $IMAGE16$. Формули (1) називаються формулами перетворення координат, а формули (2) - формулами оберненого перетворення.
Справедлива така теорема.
Теорема. Якщо перетворення (2) переводить замкнену обмежену область в замкнену обмежену область $IMAGE16$ і є взаємно однозначним, і якщо функції (1) мають в області $IMAGE16$ неперервні частинні похідні першого порядку і відмінний від нуля визначник
$IMAGE20$, (3)
а функція неперервна в області , то справедлива така формула заміни змінних
$IMAGE23$. (4)
Функціональний визначник називається визначником Якобі або якобіаном.
Таким чином, виконуючи заміну змінних в інтегралі 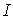за формулами (1), ми маємо елемент площі $IMAGE25$ в координатах $IMAGE26$ замінити елементом площі $IMAGE27$ в координатах $IMAGE28$ і стару область інтегрування замінити відповідною їй областю $IMAGE30$.
Розглянемо заміну декартових координат $IMAGE26$ полярними $IMAGE32$ за відомими формулами $IMAGE33$. Оскільки
$IMAGE34$.
То формула (3) набирає вигляду
$IMAGE35$ (4)
де область задана в декартовій системі координат $IMAGE37$, а $IMAGE30$ - відповідна їй область в полярній системі координат.
У багатьох випадках формулу (4) доцільно застосовувати тоді, коли підінтегральна функція або рівняння границі області містить суму $IMAGE40$, оскільки ця сума в полярних координатах має досить простий вигляд:
$IMAGE41$.
Якщо область (рис.1, а) обмежена променями, які утворюють з полярною віссю кути $IMAGE43$ та $IMAGE44$ $IMAGE45$ і кривими $IMAGE46$ та $IMAGE47$ $IMAGE48$, то полярні координати області $IMAGE30$ змінюються в межах $IMAGE50$, $IMAGE51$ (рис.1, б). Тому формулу (4) можна записати у вигляді
$IMAGE52$ (5)
$IMAGE53$
Рисунок 1 - Область: а) ; б) $IMAGE16$
подвійний інтеграл полярна координата
Якщо область охоплює початок координат, тобто точка $IMAGE57$ є внутрішньою точкою області , то
$IMAGE59$ (6)
де $IMAGE60$ - полярне рівняння межі області .
Приклади
1. Обчислити інтеграл $IMAGE62$, якщо область - паралелограм,
обмежений прямими $IMAGE64$ (рис.1, а).
Розв’язання
Безпосереднє обчислення цього інтеграла надто громіздке, тому що як в напрямі осі $IMAGE65$ так і в напрямі осі $IMAGE66$ область потрібно спочатку розбити на три області, а потім обчислювати три подвійних інтеграли.
Виконаємо таку заміну змінних: $IMAGE68$, тоді прямі $IMAGE69$ та $IMAGE70$ в системі $IMAGE37$ переходять в прямі $IMAGE72$ та $IMAGE73$ у системі $IMAGE74$ (рис.1, б), а прямі $IMAGE75$ та $IMAGE76$ відповідно в прямі $IMAGE77$ та $IMAGE78$.
Таким чином, область (паралелограм) переходить у системі $IMAGE74$ в прямокутник $IMAGE30$.
$IMAGE82$
Рисунок 2 - Область: а) ; б) $IMAGE16$
Далі маємо
$IMAGE85$
$IMAGE86$
За формулою (3)
$IMAGE87$
2. У подвійному інтегралі $IMAGE88$, де - круг, обмежений колом $IMAGE90$, перейти до полярних координат з полюсом в точці $IMAGE57$, і обчислити отриманий інтеграл.
Розв’язання
Область зображена на рис.2.
Рівняння, які пов’язують $IMAGE93$ і полярні координати $IMAGE94$ з полюсом у точці $IMAGE57$, мають вигляд $IMAGE96$, причому видно, що кут $IMAGE97$ змінюється в межах від $IMAGE98$ до $IMAGE99$.
$IMAGE100$
Рисунок 3 - Область
Підставивши вирази для $IMAGE102$ і $IMAGE103$ в рівняння кола, отримаємо $IMAGE104$, звідки $IMAGE105$ або $IMAGE106$. Ці дві криві на площині $IMAGE94$ при $IMAGE108$ обмежують область $IMAGE16$, яка є прообразом області при відображенні. Якобіан $IMAGE111$ відображення дорівнює $IMAGE112$. Підінтегральна функція $IMAGE40$ у нових змінних дорівнює $IMAGE114$. За формулою (3) маємо
$IMAGE115$.
Одержаний подвійний інтеграл за областю $IMAGE16$ зводимо до повторного:
$IMAGE117$
і обчислюємо повторний інтеграл, застосовуючи формулу Ньютона - Лейбніца:
$IMAGE118$
2. Застосування подвійних інтегралів до задач геометрії
1. Площа плоскої фігури. Якщо в площині $IMAGE37$ задана фігура, що має форму обмеженої замкненої області , то площа $IMAGE121$ цієї фігури знаходиться, як відомо, за формулою:
$IMAGE122$.
2. Об'єм тіла. Об'єм циліндричного тіла, твірні якого паралельні осі $IMAGE123$ і яке обмежене знизу областю площини $IMAGE37$, а зверху - поверхнею $IMAGE126$, де функція неперервна та невід'ємна в області , знаходиться за формулою (2):
$IMAGE129$
3. Площа поверхні. Якщо поверхня $IMAGE130$, задана рівнянням
$IMAGE131$ (7)
проектується на площину $IMAGE37$ в область (рис.3) і функції , $IMAGE135$, $IMAGE136$ неперервні в цій області, то площу $IMAGE137$ поверхні $IMAGE130$ знаходять за формулою
$IMAGE139$ (8)
$IMAGE140$
Рисунок 4 - Поверхня $IMAGE130$
Виведемо цю формулу. Розіб’ємо довільним способом область на $IMAGE143$ частин $IMAGE144$, які не мають спільних внутрішніх точок і площі яких дорівнюють $IMAGE145$. У кожній частині $IMAGE144$ візьмемо точку $IMAGE147$; на поверхні $IMAGE130$ їй відповідатиме точка $IMAGE149$, де $IMAGE150$. Через точку $IMAGE149$ проведемо дотичну площину $IMAGE152$ [3]
$IMAGE153$.
На площині $IMAGE152$ виділимо ту її частину, яка проектується на площину $IMAGE37$ в область $IMAGE144$. Позначимо цю частину дотичної площини через $IMAGE157$, а її площу - через $IMAGE158$. Складемо суму
$IMAGE159$. (9)
Границю $IMAGE137$ суми (9), коли найбільший з діаметрів $IMAGE161$ областей $IMAGE144$ прямує до нуля, назвемо площею поверхні (7), тобто за означенням покладемо
$IMAGE163$. (10)
Обчислимо цю границю. Оскільки область $IMAGE157$, яка має площу $IMAGE158$, проектується в область $IMAGE144$ з площею $IMAGE167$, то $IMAGE168$, де $IMAGE169$ - кут між площинами $IMAGE152$ та $IMAGE37$ (рис.3), тому $IMAGE172$.
Але гострий кут $IMAGE169$ дорівнює куту між віссю $IMAGE123$ і нормаллю $IMAGE175$ до дотичної площини, тобто куту між векторами $IMAGE176$та $IMAGE177$. Знайдемо за формулою (4)
$IMAGE178$.
Отже,
$IMAGE179$.
Підставляючи значення $IMAGE158$ в (10), отримуємо
$IMAGE181$.
Під знаком границі маємо інтегральну суму, складену для неперервної в області функції $IMAGE183$. Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8).
3. Застосування подвійних інтегралів до задач механіки 1. Маса пластини. Нехай на площині $IMAGE37$ маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначається неперервною функцією $IMAGE187$. Маса такої пластини визначається за формулою (1.8):
$IMAGE188$.
2. Центр маси пластини. Статичні моменти. Нехай матеріальна пластина в площині $IMAGE37$ має форму області , густина пластини в точці $IMAGE191$дорівнює $IMAGE192$, де $IMAGE192$ - неперервна функція в області Розіб'ємо область на частини $IMAGE196$, виберемо в кожній з них довільну точку $IMAGE197$ і наближено вважатимемо, що маса $IMAGE198$ частини $IMAGE144$ дорівнює $IMAGE200$, де $IMAGE167$ - площа області $IMAGE144$. Коли вважати, що кожна з цих мас зосереджена в точці $IMAGE203$, то пластину можна розглядати як систему цих матеріальних точок. Тоді координати $IMAGE204$ та $IMAGE205$ центра маси пластини наближено визначатимуться рівностями
$IMAGE206$.
Щоб знайти точні значення координат, перейдемо в цих формулах до границі при $IMAGE207$. Тоді інтегральні суми перейдуть у подвійні інтеграли і координати центра маси пластини визначатимуться формулами
$IMAGE208$. (11)
Величини
$IMAGE209$ (12)
називаються статичними моментами пластини відносно осі $IMAGE66$ та $IMAGE65$.
Враховуючи формули (8), (11) і (12), координати центра мас можна записати у вигляді
$IMAGE212$.
Якщо пластина однорідна, тобто має сталу густину $IMAGE213$, то у формулах (1.8), (11) і (12) слід покласти $IMAGE214$.
3. Моменти інерції пластини. Відомо, що момент інерції матеріальної точки відносно деякої осі дорівнює добутку маси точки на квадрат її відстані від цієї осі, а момент інерції системи матеріальних точок відносно однієї і тієї самої осі дорівнює сумі моментів інерції всіх точок системи.
Нехай матеріальна пластина має форму області у площині $IMAGE37$, а неперервна функція $IMAGE187$ визначає густину в кожній точці цієї пластини. Розіб'ємо область на частини $IMAGE144$, площі яких дорівнюють $IMAGE220$, і виберемо в кожній з цих частин довільну точку $IMAGE197$. Замінимо пластину системою матеріальних точок з масами $IMAGE222$. Якщо пластину розглядати як систему цих матеріальних точок, то моменти інерції пластини відносно осі $IMAGE66$ та відносно $IMAGE65$ наближено визначатимуться за формулами
$IMAGE225$.
Перейшовши до границі в кожній із сум при $IMAGE207$, отримуємо точні формули для обчислення моментів інерції розглядуваної пластини відносно координатних осей:
$IMAGE227$. (13)
Знайдемо момент інерції $IMAGE228$ пластини відносно початку координат.
Враховуючи, що момент інерції матеріальної точки $IMAGE229$ з масою $IMAGE230$ відносно початку координат дорівнює $IMAGE231$, аналогічно отримуємо, що
$IMAGE232$. (14)