База рефератов

Задача 1. В партии из 60 изделий 10 – бракованных. Определить вероятность того, что среди выбранных наудачу для проверки 5 изделий окажутся бракованными:

а) ровно 2 изделия;

б) не более 2 изделий.

Решение.

А)

Используя классическое определение вероятности:

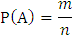
Р(А) – вероятность события А, где А – событие, когда среди выбранных наудачу изделий для проверки 5 изделий окажутся бракованными ровно 2 изделия;

m – кол-во благоприятных исходов события А;

n – количество всех возможных исходов;

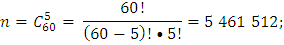
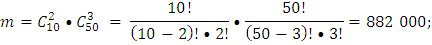
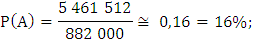
Б)

Р(А’) – вероятность события А’, где А’ – событие, когда среди выбранных наудачу изделий для проверки 5 изделий окажутся бракованными не более 2 изделий,

;

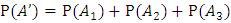$IMAGE6$

$IMAGE7$

$IMAGE8$

$IMAGE9$ – кол-во благоприятных исходов события $IMAGE10$;

$IMAGE11$ – кол-во благоприятных исходов события $IMAGE12$;

$IMAGE13$ – кол-во благоприятных исходов события $IMAGE14$;

n’ – количество всех возможных исходов;

$IMAGE15$

$IMAGE16$

$IMAGE17$

$IMAGE18$

$IMAGE19$

Ответ: вероятность того, что среди выбранных наудачу для проверки 5 изделий окажутся бракованными: а) ровно 2 изделия равна 16%. б) не более 2 изделий равна 97%.

Задача 2. В сборочный цех завода поступают детали с трех автоматов. Первый автомат дает 1% брака, второй – 2%, третий – 3%. Определить вероятность попадания на сборку небракованной детали, если с каждого автомата в цех поступило соответственно 20, 10, 20 деталей.

Решение.

По формуле полной вероятности:

$IMAGE20$

где А – взятие хорошей детали, $IMAGE21$ – взятие детали из первого (второго / третьего) автомата, $IMAGE22$ – вероятность взятия детали из первого (второго / третьего) автомата, $IMAGE23$ – вероятность взятия хорошей детали из первого (второго / третьего) автомата, $IMAGE24$ – вероятность попадания на сборку небракованной детали.

$IMAGE25$

$IMAGE26$

$IMAGE27$

$IMAGE25$

$IMAGE29$; (т. к. $IMAGE30$) = 1% = 0.01)

$IMAGE31$;

$IMAGE32$;

$IMAGE20$

$IMAGE34$

Ответ: Вероятность попадания на сборку небракованной детали равна 98%.

Задача 3. В сборочный цех завода поступают детали с трех автоматов. Первый автомат дает 1% брака, второй – 2%, третий – 3%. С каждого автомата поступило на сборку соответственно 20, 10, 20 деталей. Взятая на сборку деталь оказалась бракованной. Найти вероятность того, что деталь поступила с 1-го автомата.

Решение.

По формуле полной вероятности:

$IMAGE35$

где А’ – взятие бракованной детали, $IMAGE21$ – взятие детали из первого (второго / третьего) автомата, $IMAGE22$ – вероятность взятия детали из первого (второго / третьего) автомата, $IMAGE23$ – вероятность взятия бракованной детали из первого (второго / третьего) автомата, $IMAGE24$ – вероятность попадания на сборку бракованной детали.

$IMAGE25$

$IMAGE26$

$IMAGE27$

$IMAGE25$

$IMAGE44$; (согласно условию)

$IMAGE45$;

$IMAGE46$;

$IMAGE35$

$IMAGE48$

Согласно формуле Байеса:

$IMAGE49$

Ответ: Вероятность того, что деталь поступила с 1-го автомата равна 20%.

Задача 4. Рабочий обслуживает 18 станков. Вероятность выхода станка из строя за смену равна $IMAGE50$. Какова вероятность того, что рабочему придется ремонтировать 5 станков? Каково наивероятнейшее число станков, требующих ремонта за смену?

Решение.

Используя формулу Бернулли, вычислим, какова вероятность того, что рабочему придется ремонтировать 5 станков:

$IMAGE51$

где n – кол-во станков, m – кол-во станков, которые придётся чинить, p – вероятность выхода станка из строя за смену, q =1-р – вероятность, не выхождения станка из строя за смену.

$IMAGE52$

$IMAGE53$

$IMAGE54$

$IMAGE55$

$IMAGE56$.

Ответ: Вероятность того, что рабочему придется ремонтировать 5 станков равна 15%. Наивероятнейшее число станков, требующих ремонта за смену равно 3.

Задача 5. В двух магазинах, продающих товары одного вида, товарооборот (в тыс. грн.) за 6 месяцев представлен в таблице. Можно ли считать, что товарооборот в первом магазине больше, чем во втором? Принять $IMAGE57$= 0,05.

Все промежуточные вычисления поместить в таблице.

Магазин №1	Магазин №2
20,35	20,01
20,60	23,55
32,94	25,36
37,56	30,68
40,01	35,34
25,45	23,20

Пусть, a₁ – товарооборот в 1 магазине, a₂ – товарооборот во 2 магазине.

Формулируем гипотезы Н₀ и Н₁:

Н₀: a₁ = a₂

Н₁: a₁ ≠ a₂

	xi	xi-a1	(xi-a1)2	yi	yi-a2	(yi-a2)2
	20,35	-9,135	83,44823	20,01	-6,35	40,32
	20,6	-8,885	78,94323	23,55	-2,81	7,896
	32,94	3,455	11,93703	25,36	-1	1