Вычисление определенного интеграла
Екатеринбург
2006
Вычисление определенного интеграла
Введение
Задача численного интегрирования функций заключается в вычислении приближенного значения определенного интеграла:
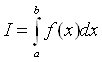 , (1)
, (1)
на основе ряда значений подынтегральной функции .{ f(x) |x=xk = f(xk) = yk}.
Формулы численного вычисления однократного интеграла называются квадратурными формулами, двойного и более кратного – кубатурными.
Обычный прием построения квадратурных формул состоит в замене подынтегральной функции f(x) на отрезке [a,b] интерполирующей или аппроксимирующей функцией g(x) сравнительно простого вида, например, полиномом, с последующим аналитическим интегрированием. Это приводит к представлению
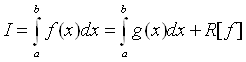
В пренебрежении остаточным членом R[f] получаем приближенную формулу
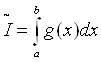 .
.
Обозначим через yi = f(xi) значение подинтегральной функции в различных точках 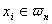 на [a,b]. Квадратурные формулы являются формулами замкнутого типа, если x0=a , xn=b.
на [a,b]. Квадратурные формулы являются формулами замкнутого типа, если x0=a , xn=b.
В качестве приближенной функции g(x) рассмотрим интерполяционный полином на 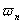 в форме полинома Лагранжа:
в форме полинома Лагранжа:
$IMAGE6$,
где
$IMAGE7$, при этом $IMAGE8$, где $IMAGE9$ - остаточный член интерполяционной формулы Лагранжа.
Формула (1) дает
$IMAGE10$, (2)
где
$IMAGE11$. (3)
В формуле (2) величины { $IMAGE12$} называются узлами, { $IMAGE13$} – весами, $IMAGE14$ - погрешностью квадратурной формулы. Если веса { $IMAGE13$} квадратурной формулы вычислены по формуле (3), то соответствующую квадратурную формулу называют квадратурной формулой интерполяционного типа.
Подведем итог.
1. Веса { $IMAGE13$} квадратурной формулы (2) при заданном расположении узлов 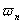 не зависят от вида подынтегральной функции.
не зависят от вида подынтегральной функции.
2. В квадратурных формулах интерполяционного типа остаточный член Rn[f] может быть представлен в виде значения конкретного дифференциального оператора на функции f(x). Для $IMAGE18$
$IMAGE19$.
3. Для полиномов до порядка n включительно квадратурная формула (2) точна, т.е. $IMAGE20$. Наивысшая степень полинома, для которого квадратурная формула точна, называется степенью квадратурной формулы.
Рассмотрим частные случаи формул (2) и (3): метод прямоугольников, трапеций, парабол (метод Симпсона). Названия этих методов обусловлены геометрической интерпретацией соответствующих формул.
Определенный интеграл функции от функции f(x): $IMAGE21$численно равен площади криволинейной трапеции, ограниченной кривыми у=0, x=a, x=b, y=f(x) (рисунок. 1).
$IMAGE22$
Рис. 1 Площадь под кривой y=f(x)
Для вычисления этой площади весь интервал интегрирования [a,b] разбивается на n равных подинтервалов длины h=(b-a)/n. Площадь под подынтегральной кривой приближенно заменяется на сумму площадей прямоугольников, как это показано на рисунке (2).
$IMAGE23$
Рис. 2 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольников
Сумма площадей всех прямоугольников вычисляется по формуле
$IMAGE24$ (4)
Метод, представленный формулой (4), называется методом левых прямоугольников, а метод, представленный формулой(5) – методом правых прямоугольников:
$IMAGE25$ (5)
Погрешность вычисления интеграла определяется величиной шага интегрирования h. Чем меньше шаг интегрирования, тем точнее интегральная сумма S аппроксимирует значение интеграла I. Исходя из этого строится алгоритм для вычисления интеграла с заданной точностью. Считается, что интегральная сумма S представляет значение интеграла I c точностью eps, если разница по абсолютной величине между интегральными суммами $IMAGE26$и $IMAGE27$, вычисленными с шагом h и h/2 соответственно, не превышает eps.
Метод средних прямоугольников
Для нахождения определенного интеграла методом средних прямоугольников площадь, ограниченная прямыми a и b, разбивается на n прямоугольников с одинаковыми основаниями h, высотами прямоугольников будут точки пересечения функции f(x) с серединами прямоугольников (h/2). Интеграл будет численно равен сумме площадей n прямоугольников (рисунок 3).
$IMAGE28$
Рис. 3 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольников
$IMAGE29$
$IMAGE30$,
n – количество разбиений отрезка [a,b].
Для нахождения определенного интеграла методом трапеций площадь криволинейной трапеции также разбивается на n прямоугольных трапеций с высотами h и основаниями у1, у2, у3,..уn, где n - номер прямоугольной трапеции. Интеграл будет численно равен сумме площадей прямоугольных трапеций (рисунок 4).
$IMAGE31$
Рис. 4 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольных трапеций.
$IMAGE30$
n – количество разбиений
$IMAGE33$
$IMAGE34$ (6)
Погрешность формулы трапеций оценивается числом
$IMAGE35$
Погрешность формулы трапеций с ростом $IMAGE36$ уменьшается быстрее, чем погрешность формулы прямоугольников. Следовательно, формула трапеций позволяет получить большую точность, чем метод прямоугольников.
Если для каждой пары отрезков $IMAGE37$ построить многочлен второй степени, затем проинтегрировать его на отрезке $IMAGE37$ и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.
В методе Симпсона для вычисления определенного интеграла весь интервал интегрирования [a,b] разбивается на подинтервалы равной длины h=(b-a)/n. Число отрезков разбиения является четным числом. Затем на каждой паре соседних подинтервалов подинтегральная функция f(x) заменяется многочленом Лагранжа второй степени (рисунок 5).
$IMAGE39$
Рис. 5 Функция y=f(x) на отрезке $IMAGE37$ заменяется многочленом 2-го порядка
$IMAGE41$Рассмотрим подынтегральную функцию $IMAGE42$ на отрезке $IMAGE43$. Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с y= $IMAGE42$ в точках $IMAGE45$:
$IMAGE46$
Проинтегрируем $IMAGE47$на отрезке $IMAGE43$.:
$IMAGE49$
Введем замену переменных:
$IMAGE50$
Учитывая формулы замены,
$IMAGE51$
$IMAGE41$Выполнив интегрирование, получим формулу Симпсона:
$IMAGE53$
Полученное для интеграла $IMAGE54$ значение совпадает с площадью криволинейной трапеции, ограниченной осью $IMAGE55$, прямыми $IMAGE56$, $IMAGE57$ и параболой, проходящей через точки $IMAGE58$ На отрезке $IMAGE59$формула Симпсона будет иметь вид:
$IMAGE60$
В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3, ..., х2n-1 имеет коэффициент 4, в четных точках х2, х4, ..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, хn =b - коэффициент 1.
Геометрический смысл формулы Симпсона: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами.
Если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем
$IMAGE61$
где М - наибольшее значение $IMAGE62$ на отрезке [a, b]. Так как n4 растет быстрее, чем n2, то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций.
Пример
Вычислим интеграл $IMAGE63$
Этот интеграл легко вычисляется: $IMAGE64$
Возьмем n равным 10, h=0.1, рассчитаем значения подынтегральной функции $IMAGE65$ в точках разбиения $IMAGE66$, а также полуцелых точках $IMAGE67$.
По формуле средних прямоугольников получим Iпрям=0.785606 (погрешность равна 0.027%), по формуле трапеций Iтрап=0.784981 (погрешность около 0,054. При использовании метода правых и левых прямоугольников погрешность составляет более 3%.
Для сравнения точности приближенных формул вычислим еще раз интеграл
$IMAGE68$,
но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках: у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.
По формуле Симпсона получаем
$IMAGE69$
Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f(4)(x)=24/(1+x)5 , откуда следует, что на отрезке [0, 1] $IMAGE70$. Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 44)=0.0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.
Сравнение методов по точности
Сравним методы по точности, для этого произведем вычисления интеграла функций y=x, y=x+2, y=x2, при n=10 и n=60, a=0, b=10. Точное значение интегралов составляет соответственно: 50, 70, 333.(3)
таблица 1
| метод | n | x | x+2 | x2 |
| Метод средних прямоугольников | 10 | 50 | 70 | 332.5 |
| Метод правых прямоугольников | 10 | 45 | 65 | 285 |
| Метод трапеции | 10 | 50 | 70 | |