Министерство образования и науки Украины
Кафедра КИТ
“ВЕРОЯТНОСТНЫЕ ПРОЦЕССЫ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ”
2008
РЕФЕРАТ
Пояснительная записка к расчетно-графической работе: 29 стр., 9 рис., 1 прил., 5 источников.
Объект исследования – оптимальный предел прочности алюминиевых деформируемых сплавов при испытании на растяжение.
Метод исследования – применение математико-статистических методов в автоматизированных системах, реализация программ статистической обработки эксперимента на ЭВМ.
Многие детали и конструкции испытывают нагрузки на растяжение. При чем эти нагрузки часто являются основным фактором, влияющим на выход из строя деталей и конструкций. Поэтому очень важной и актуальной является задача нахождения оптимального состава материала, в течение длительного времени испытующего нагрузки на растяжение.
ДЕФОРМИРУЕМЫЙ АЛЮМИНИЕВЫЙ СПЛАВ, ЛИТИЙ, ТЕМПЕРАТУРА СТАРЕНИЯ, ВРЕМЯ СТАРЕНИЯ, МНОГОФАКТОРНЫЙ ЭКСПЕРИМЕНТ.
СОДЕРЖАНИЕ
Введение
1 Постановка задачи
2 Этапы планирования и статической обработки результатов эксперимента для построения модели 2-го порядка
2.1 Построение модели плана II порядка
2.2 Кодирование факторов
2.3 Составление план – матрицы
2.4 Проверка воспроизводимости опытов
2.5 Расчет коэффициентов регрессии
2.6 Определение значимости коэффициентов
2.7 Проверка адекватности модели
3 Выбор и описание метода условной оптимизации
3.1 Выбор метода условной оптимизации
3.2 Описание метода условной оптимизации (Фиако-МакКормика)
4 Описание программы
4.1 Общие сведения
4.2 Функциональное назначение
4.3 Описание логической структуры программы
4.4 Используемые технические средства
4.5 Вызов и загрузка
4.6 Входные данные
4.7 Выходные данные
5 Результаты обработки данных эксперимента
6 Графики зависимости отклика
7 Кривые равного выхода
Заключение
Список использованных источников
Приложение
Введение
Развитие современной техники связано с созданием новых и постоянным совершенствованием существующих технологических процессов. Основой их разработки и оптимизации является эксперимент. Заметное повышение эффективности экспериментальных исследований и инженерных разработок достигается использованием математических методов планирования экспериментов. Использование математико-статистических методов при постановке задач. В процессе экспериментирования и при обработке полученных данных существенно сокращает сроки решения, снижает затраты на исследования и повышает качество полученных результатов.
Встречающиеся на практике реальные задачи весьма разнообразны. Достаточно грубо их можно разделить на три основных задачи:
1 Выявление количественных зависимостей между параметрами процесса – задачи описания;
2 Определение оптимальных условий протекания процесса – экстремальные задачи;
3 Выбор оптимального состава многокомпонентных смесей.
Часто, приступая к изучению какого-либо процесса экспериментатор не имеет исчерпывающих сведений о механизме процесса. Можно только указать параметры определяющие условия протекания процесса, и, возможно требования к его результатам. Поставленная проблема является задачей кибернетики. Действительно, если считать кибернетику «наукой, изучающей системы любой природы, способные воспринимать, хранить и перерабатывать информацию для целей оптимального управления» [1], то такую систему можно представить в виде черного ящика.
Черный ящик – объект исследования, имеющий (k+p) входов и m выходов.
X – управляемые параметры, Z – неуправляемые параметры.
Зависимость между выходными параметрами (откликом) и входными параметрами (факторами) называется функцией отклика.
Математическая запись функции отклика представлена в виде формулы (1):
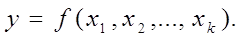 (1)
(1)
Этому уравнению в многомерном пространстве соответствует гипперповерхность, которая называется поверхностью отклика, а само пространство – факторным пространством.
Эксперимент можно проводить по разному. В случае, когда исследователь наблюдает за каким-то неуправляемым процессом, не вмешиваясь в него, или выбирает экспериментальные точки интуитивно, на основании каких-то привходящих обстоятельств, эксперимент считают пассивным. В настоящее время пассивный эксперимент считается неэффективным.
Гораздо более продуктивно проводится эксперимент, когда исследователь применяет статистические методы на всех этапах исследования, и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в процессе экспериментирования, при обработке результатов и после эксперимента, принимая решение о дальнейших действиях. Такой эксперимент считают активным, и он предполагает планирование эксперимента.
Под планированием эксперимента понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Основные преимущества активного эксперимента связаны с тем, что он позволяет:
1 Минимизировать общее число опытов;
2 Выбирать четкие логически обоснованные процедуры, последовательно выполняемые экспериментатором при проведении исследования;
3 Использовать математический аппарат, формализующий многие действия экспериментатора;
4 Одновременно варьировать всеми переменными и оптимально использовать факторное пространство;
5 Организовать эксперимент таким образом, чтобы выполнялись многие исходные предпосылки регрессионного анализа;
6 Получать математические модели, имеющие лучшие в некотором смысле свойства по сравнению с моделями, построенными из пассивного эксперимента;
7 Рандомизировать условия опытов, то есть многочисленные мешающие факторы превратить в случайные величины;
8 Оценивать элемент неопределенности, связанный с экспериментом, что дает возможность сопоставлять результаты, полученные разными исследователями [1].
Целью данной работы является освоение анализа плановых экспериментов и анализ данных, полученных при выполнении этих экспериментов.
1. Постановка задачи Изучали механические свойства одного из алюминиевых деформируемых сплавов в зависимости от содержания в нем лития Х1 (основной уровень 1%, интервал варьирования 0,5%), температуры старения Х2 (основной уровень 175 гр.С, интервал варьирования 25 гр.С) и времени старения Х3 (основной уровень 4 ч., интервал варьирования 2 ч.). В качестве отклика выбран предел прочности сплавов, определяющийся при испытании на растяжение (Y, кгс/кв.мм).
Задание на расчетно-графическую работу:
1) Найти уравнение регрессии 2-го порядка и выполнить статистический анализ модели.
2) Исследовать модель 2-го порядка на выпуклость и вогнутость методами дифференциального исчисления.
3) Определить тип поверхности отклика.
4) Построить графики зависимости отклика от каждого из факторов Y=f(Xi) при фиксированных значениях остальных факторов (каждый рисунок должен содержать 3-4 кривые).
5) Применяя один из методов оптимизации, найти в исследованной области оптимальные сочетания факторов, обеспечивающие максимальное и минимальное значения отклика.
6) Построить двумерные сечения поверхности отклика, соответствующие пересечению поверхности с плоскостями Xi=Ximax. Для этого в уравнение регрессии необходимо подставить значение этого фактора, и по полученным двухфакторным уравнениям рассчитать, а потом построить изолинии поверхности отклика (кривые равного выхода).
7) Определить типы кривых равного выхода.
8) Используя двумерные сечения поверхности, выполнить анализ влияния факторов в изученных интервалах их изменения на функцию отклика.
2. Этапы планирования и статической обработки результатов эксперимента для построения модели 2-го порядка
2.1 Построение модели плана II порядка
Для построения плана II порядка можно использовать следующую модель:
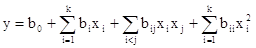 (2)
(2)
Для этого необходимо провести эксперимент так, чтобы каждый фактор варьировался на трех уровнях. Простейшим решением этой задачи является план типа 3k. Реализация этого плана для k>3 требует большого числа опытов.
Для построения модели второго порядка обычно используют ортогональный план первого порядка в качестве ядра, на котором достраивается план второго порядка, поэтому такие планы называются композиционными и соответствуют шаговой идее построения планов.
Для удобства работы с приведенной моделью II порядка, с помощью обозначений (3) преобразуем ее к виду (2’):
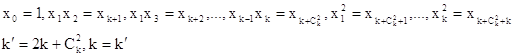 (3)
(3)
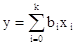 (2’)
(2’)
Задача заключается в том, чтобы по результатам наблюдений определить значения коэффициентов bi, дисперсии и доверительные границы для них, а также определить их значимость.
Согласно МНК, для нахождения коэффициентов bi, необходимо минимизировать функцию:
$IMAGE6$ (4)
где N – количество опытов;
xui –значение i-й переменной в u-м опыте;
yu – значение экспериментальных y в u-м опыте;
Из условия минимизации функции ss, можно получить систему нормальных уравнений МНК:
$IMAGE7$ (5)
Представив все результаты в матричной форме, получим:
$IMAGE8$, $IMAGE9$, $IMAGE10$, (6)
где X – матрица условий эксперимента; Y – матрица результатов опытов; B – матрица коэффициентов.
Умножив транспонированную матрицу X на матрицу X, получим матрицу системы нормальных уравнений, которая называется информационной матрицей Фишера (матрицей моментов):
$IMAGE11$ (7)
Умножив транспонированную матрицу X на матрицу Y, получим:
$IMAGE12$ (8)
Используя данные обозначения, систему нормальных уравнений можно записать в матричной форме:
$IMAGE13$ (9)
Обозначая обратную матрицу моментов как:
$IMAGE14$ (10)
получим выражение для матрицы коэффициентов:
$IMAGE15$ (11)
Все статистические свойства коэффициентов линии регрессии определяется матрицей дисперсий ковариаций.
$IMAGE16$ (12)
где cov(bi, bj) – ковариации коэффициентов bi, и bj;
S2(bi) – дисперсия коэффициента bi;
S2(y) – дисперсия опыта.
Дисперсию опыта можно определить по формулам:
$IMAGE17$ (13)
$IMAGE18$ (14)
где m – количество параллельных опытов.
Если параллельные опыты не проводятся, то для оценки дисперсии опыта ставятся эксперименты в центре плана. Тогда дисперсия определяется по формуле:
$IMAGE19$ (15)
где $IMAGE20$ - количество опытов в центре плана.
Так как ядро плана ортогонально, то для сохранения ортогональности композиционного плана необходимо при построении матрицы планирования обеспечить условия:
$IMAGE21$
Величина $IMAGE22$ зависит от фактора и от плеча d:
$IMAGE23$;
Для k=3 ядро =15, $IMAGE22$=11/15=0.7303, d=1.2154
2.2 Кодирование факторов
Кодирование факторов используется для перевода натуральных факторов в безразмерные величины, чтобы построить стандартную план – матрицу эксперимента.
Для перевода заполняется таблица кодирования факторов на двух уровнях. В качестве 0-го уровня обыч