База рефератов

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Федеральное образовательное учреждение

высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Д.Н. Карпинский

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к разделу «Традиционные методы вычислительной томографии» спецкурса «Применение томографических методов в медицинской диагностике»

для студентов специальности «Прикладная математика»

Ростов-на-Дону

2007

Печатается по решению кафедры теории упругости факультета математики, механики и компьютерных наук ЮФУ, протокол N1 от 10 сентября 2007 года.

Методические указания разработаны доктором физико-математических наук, профессором кафедры теории упругости Д.Н.Карпинским.

1. ВВЕДЕНИЕ

Томография - одно из бурно развивающихся направлений в области получения и обработки информации. Томография позволяет заглянуть внутрь наблюдаемого объекта. Основная проблема томографии - как по получаемым в томографическом эксперименте проекционным данным (например, по рентгеновским снимкам) "увидеть" внутреннюю структуру анализируемого объекта. Область математики, в которой разрабатываются методы решения подобных задач, известна как "интегральная геометрия" [1].

Хронология развития вычислительной томографии:

1895 г. – открытие рентгеновских лучей;

1917 г. – преобразование Радона;

1920 г. – рентгенограмма в медицине;

1930 г. – линейная томография, вращательная томография;

1942 г. – РВТ в радиоастрономии;

1961 г. – сверточный алгоритм;

1964 г. – алгоритм РВТ А. Кормака;

1972 г. – серийный томограф Г. Хаунсфилда;

1977 г. – учебный курс по вычислительной томографии в университете штата Нью-Йорк;

1979 г. – Нобелевская премия А. Кормаку и Г. Хаунсфилду.

1.2 В настоящее время существуют следующие виды томографии:

1) рентгеновская томография;

2) радионуклеидная томография;

3) ЯМР – томография;

4) ультразвуковая томография;

5) оптическая томография;

6) протонно-ионная томография;

7) томография в радиодиапазоне;

8) ЭПР - томография.

Особенно важное значение методы томографии имеют для медицинской диагностики [2].

Все виды томографии по свойствам изучаемых объектов можно разделить на два больших класса: трансмиссионную вычислительную томографию (ТВТ) и эмиссионную вычислительную томографию (ЭВТ). В ТВТ внешнее излучение зондирует пассивный (неизлучающий) объект, частично поглощаясь им. В ЭВТ активный (излучающий) объект представляет собой пространственное распределение источников излучения, при этом выходящее вдоль какого-либо направления излучение является суперпозицией излучений всех источников, лежащих на линии проецирования.

Рассмотрим вначале физический закон распространения внешнего излучения в веществе. Пусть тонкий пучок, например 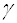- излучения, с интенсивностью  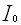падает на слой вещества с распределением линейного коэффициента поглощения (ослабления)  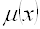вдоль распространения пучка. При этом феноменологически  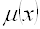определяют через вероятность  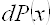поглощения 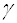- кванта при прохождении элементарного пути $IMAGE7$ соотношением $IMAGE8$.

$IMAGE9$

$IMAGE10$Рисунок 1. К выводу уравнения переноса излучения (1.1).

Стационарное уравнение переноса излучения в чисто поглощающей неоднородной среде, описывающее процесс излучения в веществе, представляет собой баланс частиц или энергии и имеет вид

$IMAGE11$ (1.1)

Решением уравнения (2.1) будет закон Бугера-Ламберта-Бэра для неоднородной поглощающей среды, который составляет основу расчетов ТВТ.

$IMAGE12$ , (1.2)

где $IMAGE13$ - интенсивность источника излучения.

Рассмотрим теперь закон распространения излучения при действии внутренних источников излучения (самоизлучающие объекты).

$IMAGE14$

Рисунок 2. К выводу закона переноса излучения при действии внутреннего источника.

Пусть точечный источник излучает в телесный угол $IMAGE15$ с интенсивностью 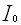 в веществе с распределением линейного коэффициента ослабления  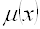вдоль прямой, соединяющей источник с небольшой площадкой $IMAGE18$, наклоненной под углом $IMAGE19$ к этой прямой. Тогда для интенсивности $IMAGE20$, приходящейся на площадку $IMAGE18$, получаем [3]

$IMAGE22$ . (1.3)

Выражение (1.3) учитывает четыре основных фактора: пространственное распределение источника излучения, геометрическое ослабление, ослабление излучения в веществе и наклон площадки детектора. Формула (1.3) лежит в основе ЭВТ.

2. ПРЕОБРАЗОВАНИЕ РАДОНА

2.1 Рассмотрим задачу восстановления двумерного распределения коэффициента ослабления $IMAGE23$ при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол $IMAGE24$, и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение $IMAGE23$. Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.

$IMAGE26$

Рисунок 3. Схема кругового сканирования с параллельными проекциями.

Пусть на плоскости, где введена прямоугольная система координат $IMAGE27$ задана функция $IMAGE28$. Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим $IMAGE29$, зависит от того, по какой именно прямой проводится интегрирование.

$IMAGE30$

Рисунок 4. К выводу формул преобразования Радона.

Известно, что всякая прямая может быть описана уравнением

$IMAGE31$, (2.1)

где $IMAGE32$ - расстояние от начала координат до этой прямой; $IMAGE33$ - угол, образованный с осью $IMAGE34$ перпендикуляром, опущенным из начала координат на эту прямую.

Произвольная прямая $IMAGE35$ однозначно задается двумя параметрами $IMAGE32$ и $IMAGE33$. Поэтому и результат интегрирования функции $IMAGE28$ по некоторой прямой будет зависеть от этих же параметров, т.е. $IMAGE39$. Предположим, что функция $IMAGE28$ интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции $IMAGE28$ на плоскости $IMAGE27$ ставит в соответствие функцию $IMAGE39$ на множестве всех прямых, задаваемую интегралами от $IMAGE28$ вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию $IMAGE39$ часто называют образом функции $IMAGE28$ в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид

$IMAGE47$. (2.2)

Задача ставится следующим образом: функция $IMAGE28$ неизвестна, но известна функция $IMAGE39$, являющаяся образом $IMAGE28$ в пространстве Радона; требуется по функции $IMAGE39$ определить $IMAGE28$. Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.

Согласно определению радоновского образа и с учетом того, что интеграл от заданной функции вдоль прямой равен интегралу по всей плоскости произведения этой функции на $IMAGE53$- функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]

$IMAGE54$. (2.3)

Интегрирование, осуществляемое по двум переменным, можно свести к интегрированию по одной переменной. Для этого введем еще одну прямоугольную систему координат $IMAGE55$, повернутую относительно $IMAGE27$ на угол $IMAGE33$. Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:

$IMAGE58$  $IMAGE59$ (2.4)

$IMAGE60$  $IMAGE61$ (2.5)

Сделаем в (2.3) замену переменных (2.4)

$IMAGE62$=

= $IMAGE63$ (2.6)

Для функции $IMAGE28$, отличной от нуля в пределах некоторой ограниченной области, ее радоновский образ также определяется выражением (2.3), только интегрирование проводится не по всей плоскости, а задается границами данной области. Так, если $IMAGE28$ отлична от нуля внутри круга радиуса $IMAGE66$, то вместо (2.6) имеем

$IMAGE67$. (2.7)

В общем случае функция, описывающая радоновский образ, обладает одним важным свойством

$IMAGE68$. (2.8)

Физический смысл этого свойства состоит в том, что любые пары $IMAGE69$ и $IMAGE70$ согласно (2.1) задают одну и ту же прямую.

Приведем примеры, которые иллюстрируют вычисление радоновских образов.

Пример 1.

Пусть $IMAGE71$. Подставим это выражение в (2.6) и получим (см. Приложение А)

$IMAGE72$=

= $IMAGE73$. (2.9)

Из (2.9) следует, что если функция $IMAGE28$ отлична от нуля в точке $IMAGE75$, то функция, описывающая ее образ в пространстве Радона $IMAGE39$, отлична от нуля на линии

$IMAGE77$, (2.10)

	$IMAGE78$

 где $IMAGE79$.

$IMAGE80$

Рисунок 5. $IMAGE53$- функция (а) и ее радоновский образ (б)

Пример 2.

Пусть $IMAGE82$. Подставляя это выражение в (2.6), получим

$IMAGE83$ . (2.11)

			$IMAGE84$
	$IMAGE85$

Рисунок 6. Функция (а) и ее радоновский образ (б)

Область, где $IMAGE86$ принимает максимальные значения, представляет собой линию, которая определяется выражением (2.10).

Пример 3.

При $IMAGE87$ (2.12)

получаем

$IMAGE88$ (2.13)

	$IMAGE89$
			$IMAGE90$

Рисунок 7. Функция (а) и ее радоновский образ (б)

2.2 В случае самоизлучающего объекта основной задачей ЭВТ является задача восстановления двумерного распределения источников излучения $IMAGE91$. Для простоты будем считать, что область, в которой распределены источники излучения, целиком расположена в области поглощения излучения, характеризующейся функцией распределения коэффициента ослабления $IMAGE28$. Обычно при измерениях с помощью ЭВТ, также как и при ТВТ, используют круговую схему с параллельными проекциями.

$IMAGE93$

Рисунок 8. Круговая геометрия измерений в ЭВТ.

В [3] показано, что для ЭВТ с постоянным коэффициентом ослабления $IMAGE94$ экспоненциальное преобразование Радона в декартовых координатах имеет вид

$IMAGE95$, (2.14)

а в полярных координатах

$IMAGE96$. (2.15)

Выражение (2.15) можно переписать в другом виде

$IMAGE97$. (2.16)

2.3 Выражения (2.3), (2.6) позволяет по функции $IMAGE28$ найти ее радоновский образ $IMAGE39$. Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть $IMAGE100$ - одномерное преобразование Фурье функции $IMAGE39$ по переменной $IMAGE32$, а $IMAGE103$ - двумерное преобразование Фурье функции $IMAGE28$ по переменным $IMAGE105$. Согласно определению

$IMAGE106$, (2.17)

$IMAGE107$. (2.18)

В трехмерном пространстве введем прямоугольную систему координат, у которой по одной оси отложены значения $IMAGE108$, а по двум другим – значения $IMAGE109$ и $IMAGE110$.

$IMAGE111$

Рисунок 9. Центральное сечение двумерного преобразования Фурье

Проведем плоскость, перпендикулярную плоскости $IMAGE112$ и проходящую через начало координат, такую, что линия ее пересечения с плоскостью $IMAGE112$ составляет с осью $IMAGE109$ угол, равный $IMAGE33$ (центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции $IMAGE103$ получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно $IMAGE117$, координаты точки этой прямой в плоскости $IMAGE112$ равны $IMAGE119$ и $IMAGE120$. Следовательно, $IMAGE103$ подстановкой $IMAGE119$, $IMAGE120$ превращается в $IMAGE124$.

Теорема.

Пус