Сургутский государственный педагогический институт
Кафедра высшей математики
По дисциплине:
ИСТОРИЯ МАТЕМАТИКИ
На тему:
ТЕОРИЯ ФЛЮКСИЙ
Выполнил:
Студентка гр. 751,
Митющенко Е.В.
Проверил:
преподаватель
Ефремова Т.Н.
Сургут, 2000.
Оглавление
Введение. 2
§ 1. Общие положения теории флюксий. 3
§ 2. Решение проблем теории флюксий. 6
Решение первой проблемы.. 7
Решение второй проблемы.. 7
Частное решение. 7
Подготовление к решению. 9
Классификация уравнений в рамках проблемы и их решение. 12
Решение первого случая. 12
Решение второго случая. 12
Заключение. 16
Литература: 17
Введение К последней трети 17 века относится открытие дифференциального и интегрального исчисления в собственном смысле слова. В отношении публикации приоритет этого открытия принадлежит Г. Лейбницу, давшему развёрнутое изложение основных идей нового исчисления в статьях, опубликованных в 1682-86. В отношении же времени фактического получения основных результатов имеются все основания считать приоритет принадлежащим И. Ньютону, который к основным идеям дифференциального и интегрального исчисления пришёл в течение 1665-66.
"Анализ с помощью уравнений" И. Ньютона в 1669 был передан им в рукописи английским математикам И. Барроу и Дж. Коллинзу и получил широкую известность среди английских математиков. "Метод флюксий" - сочинение, в котором И. Ньютон дал вполне законченное систематическое изложение своей теории, - был написан в 1670-71 (издан в 1736). Г. Лейбниц же начал свои исследования по анализу бесконечно малых лишь в 1673.
И. Ньютон и Г. Лейбниц впервые в общем виде рассмотрели основные для нового исчисления операции дифференцирования и интегрирования функций, установили связь между этими операциями (так называемая формула Ньютона - Лейбница) и разработали для них общий единообразный алгоритм.
Подход к делу у И. Ньютона и Г. Лейбница, однако, различен. Для И. Ньютона исходными понятиями являются понятия "флюенты" (переменной величины) и её "флюксий" (скорости её изменения).
§ 1. Общие положения теории флюксий Основные задачи теории Ньютон формулировал в терминах механики:
1) определение скорости движения по известной зависимости пути от времени; «Длина проходимого пути постоянно (т. е. в каждый момент времени) дана; требуется найти скорость движения в предложенное время»
2) определение пройденного за данное время пути по известной скорости. «Скорость движения постоянно дана; требуется найти длину пройденного в предложенное время пути»
Прямой задаче нахождения флюксий и соотношений между флюксиями по заданным флюентам (дифференцирование и составление дифференциальных уравнений) Ньютон противопоставлял обратную задачу нахождения флюент по заданным соотношениям между флюксиями, то есть сразу общую задачу интегрирования дифференциальных уравнений; задача нахождения первообразной появляется здесь как частный случай интегрирования дифференциального уравнения
dy/dx = f(x).
Такая точка зрения была вполне естественна для Ньютона как создателя математического естествознания: его исчисление флюксий являлось просто отражением той идеи, что элементарные законы природы выражаются дифференциальными уравнениями, а предсказание хода описываемых этими уравнениями процессов требует их интегрирования. Для Лейбница в центре внимания находился вопрос о переходе от алгебры конечного к алгебре бесконечно малых; интеграл воспринимался прежде всего как сумма бесконечно большого числа бесконечно малых, а основным понятием дифференциального исчисления являлись дифференциалы - бесконечно малые приращения переменных величин (наоборот, И. Ньютон, вводя соответствующее понятие "момента", стремился в более поздних работах от него освободиться).
С публикации работ Г. Лейбница в континентальной Европе начался период интенсивной коллективной работы над дифференциальным и интегральным исчислением, интегрированием дифференциальных уравнений и геометрическими приложениями анализа, в которой принимали участие, кроме самого Г. Лейбница, Я. Бернулли, И. Бернулли, Г. Лопиталь и другие. Здесь создаётся современный стиль математической работы, при котором полученные результаты немедленно публикуются в журнальных статьях и уже очень скоро после опубликования используются в исследованиях других учёных.
Основные идеи метода флюксий сложились у Н. под влиянием трудов П. Ферма, Дж. Валлиса и его учителя И. Барроу в 1665-66. К этому времени относится открытие Ньютоном взаимно обратного характера операций дифференцирования и интегрирования.
В понятиях и терминологии метода флюксий с полной отчётливостью отразилась глубокая связь математических и механических исследований Ньютона. Понятие непрерывной математической величины Ньютон вводит как абстракцию от различных видов непрерывного механического движения. Линии производятся движением точек, поверхности - движением линий, тела - поверхностей, углы - вращением сторон и т.д. Переменные величины Ньютон назвал флюентами (текущими величинами, от лат. fluo - теку). Общим аргументом текущих величин - флюент - является у Ньютона "абсолютное время", к которому отнесены прочие, зависимые переменные. Скорости изменения флюент Ньютон назвал флюксиями, а необходимые для вычисления флюксий бесконечно малые изменения флюент - "моментами" (у Лейбница они назывались дифференциалами). Таким образом, Ньютон положил в основу понятия флюксий (производной) и флюенты (первообразной, или неопределённого интеграла). И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) в виде
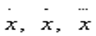 и для бесконечно малого приращения o
и для бесконечно малого приращения o
Время Ньютон понимал как общий аргумент, к которому отнесены все переменные величины. Систему величин х, у, z,..., одновременно изменяющихся непрерывно в зависимости от времени, он называл флюентами (лат. fluens – текущий, от fluo – теку), скорости, с которыми изменяются флюенты, – флюксиями (лат. fluxio – истечение): 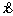 ,
, 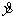 ,
, 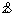 . Т. о., флюксии являются производными флюент по времени. Бесконечно малые изменения флюент Ньютон назвал моментами (понятие момента в Ф. и. соответствует дифференциалу), момент независимого переменного он обозначил знаком о, момент флюенты х – знаком xo.
. Т. о., флюксии являются производными флюент по времени. Бесконечно малые изменения флюент Ньютон назвал моментами (понятие момента в Ф. и. соответствует дифференциалу), момент независимого переменного он обозначил знаком о, момент флюенты х – знаком xo.
Представление о существе операции отыскания флюксий, особенностях символики и о ходе рассуждений Ньютона можно получить из следующих примеров:
Пример 1.
«Если соотношение между текущими величинами x и y выражается уравнением
| f(x,y) = x3 + ax2 + axy y3 = 0, | |
то сперва расположи члены по x, а затем по y и помножь их, как указано ниже( Звездочкой Ньютон обозначает члены, которые можно отбросить, но которые потребуются в дальнейшем. ).
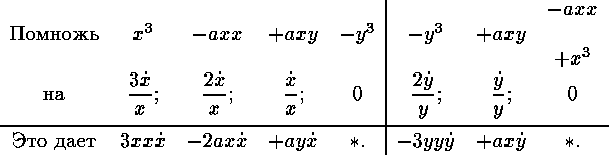
Сумма произведений есть
$IMAGE6$
и это уравнение показывает, какое соотношение существует между флюксиями $IMAGE7$ и $IMAGE8$. (У Ньютона нет других формул, кроме
Нет у него формул производной произведения, дроби и сложной функции. (В "Математических началах натуральной философии", впрочем, дается формула для момента произведения.) Что производная суммы равняется сумме производных слагаемых, представляется ему совершенно очевидным. Основное правило Ньютона это не что иное, как правило определения производной полинома f(x, y) по t, когда x, y суть функции от t (t у него время). Мы будем писать, если
| f(x,y) = x3 + ax2 + axy y3 = 0, | |
что $IMAGE9$,
где $IMAGE10$ $IMAGE11$
Ньютон предлагают находить эти $IMAGE12$ , $IMAGE13$ следующим образом: члены с x3, x2, x, x0 умножаются на 3xx’/x, 2xx’/x, xx’/x, 0/x, а члены с y2, y, y0 на 2yy’/y, yy’/y, 0/y)»
§ 2. Решение проблем теории флюксий В "Методе флюксий..." (1670-1671) Ньютон формулирует две основные взаимно-обратные задачи анализа:
1) определение скорости движения в данный момент времени по известному пути, или определение соотношения между флюксиями по данному соотношению между флюентами (Современная формулировка: какому дифференциальному уравнению удовлетворяют функции (независимого аргумента), связанные некоторым функциональным уравнением? Или: как дифференцировать неявно заданную функцию?),
2) определение пройденного за данное время пути по известной скорости движения, или определение соотношения между флюентами по данному соотношению между флюксиями (задача интегрирования дифференциального уравнения и, в частности, отыскания первообразных, найти общее (или хотя бы частное) решение дифференциального уравнения).
Решение первой проблемы Ньютон предлагает в следующем виде:
«Расположи уравнение, которое выражает данное соотношение, по степеням какой-либо из входящих в него текущих величин (например x) и члены его помножь на какую-либо арифметическую прогрессию, а затем на $IMAGE14$ . Это действие произведи отдельно для каждой из текущих величин. Затем положи сумму всех этих произведений равной нулю, и ты получишь искомое уравнение». Данная рекомендация иллюстрируется примерами, аналогичными примеру 1.
Для решения второй проблемы Ньютон предлагает следующие шаги:
«Так как эта проблема обратна вышеизложенной, то ее можно решать с помощью противоположных действий, а именно, члены помноженные на $IMAGE7$, должны быть расположены по степеням x и поделены на $IMAGE14$ , а затем - на показатели их степеней или же на какую-либо другую арифметическую прогрессию. После того как эти действия будут произведены и для членов, помноженных на $IMAGE17$, $IMAGE8$или $IMAGE19$, получившуюся при этом сумму по отбрасывании лишних членов следует положить равной нулю.
Пример 2.
Предложено уравнение
$IMAGE6$
Действие производится следующим образом:
$IMAGE21$
Поэтому сумма
выражает искомое соотношение величин x и y.
Здесь следует заметить, что хотя член axy встречается дважды, я все же не выписываю его дважды в сумме
но один из них отбрасываю как лишний. Таким образом, если какой-либо член встречается дважды (или еще больше раз в том случае, если он получается от различных флюэнт), то в сумме членов его следует выписывать лишь один раз.»
( Здесь описана следующая процедура нахождения частного решения дифференциального уравнения