Терема Ферма. Бесконечный спуск для нечётных показателей n.
Получены другие формулы для решений уравнения Пифагора x^2+y^2=z^2, отличные от формул древних индусов, и делающие возможным доказательство для всех нечётных значений показателя n тем же способом бесконечного спуска Ферма, что и для n=4.
Ферма (потом Эйлер) доказывали эту теорему для частного случая n = 4 способом бесконечного спуска с помощью формул древних индусов: x= a 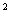 - b
- b 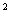 , y=2ab, z= a
, y=2ab, z= a 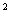 + b
+ b 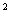 .
.
Другие формулы: x = 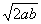 + b, y =
+ b, y = 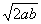 + a, z =
+ a, z = 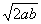 + a + b (1).
+ a + b (1).
В (1) a и b любые взаимно простые положительные целые числа, одно из них – чётное, другое – нечётное. Пусть a – чётное, b – нечётное: a=2c $IMAGE8$, b=d $IMAGE8$, откуда 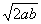 =2cd.
=2cd.
После подстановки значений a и b в (1) получим:
X = d(2c+d); Y= 2c(c+d); Z= 2c(c+d)+ d $IMAGE8$ (2),
где c и d любые целые положительные числа; c,d и их суммы взаимно просты;
X,Y,Z – взаимно простые тройки решений уравнения Пифагора. Если определены и целы c и d, то определены и целы все три числа X,Y,Z.
Предположим, что уравнение Ферма x $IMAGE12$+ y $IMAGE12$= z $IMAGE12$ имеет тройку целых положительных решений x,y,z при нечётном целом положительном значении показателя n, n>2. Запишем это уравнение следующим образом:
(x $IMAGE15$) 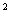 + (y $IMAGE15$)
+ (y $IMAGE15$) 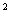 = (z $IMAGE15$)
= (z $IMAGE15$) 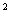 (4).
(4).
Так как рассматривается возможность существования целых решений уравнений Ферма и (4) , то должно выполняться следующее условие:
x $IMAGE15$= X; y $IMAGE15$= Y; z $IMAGE15$= Z; где X,Y,Z из (2) (5).
Чтобы числа x,y,z были целыми, из всех трёх чисел X,Y,Z должны извлекаться целочисленные корни степени n (n – нечётное положительное целое число):
x = $IMAGE24$= ( $IMAGE25$) 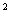 ; y = $IMAGE27$= ( $IMAGE28$)
; y = $IMAGE27$= ( $IMAGE28$) 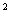 ; z = $IMAGE30$.
; z = $IMAGE30$.
Для упрощения достаточно рассмотреть два целых числа $IMAGE25$ и $IMAGE28$ ( n – нечётное ):
$IMAGE25$ = $IMAGE34$= $IMAGE35$ и $IMAGE28$= $IMAGE37$= $IMAGE38$.
Подкоренные выражения содержат сомножители не имеющие общих делителей, кроме 1, поэтому каждый сомножитель должен являться целым числом в степени n:
d = g $IMAGE39$; 2 c = h $IMAGE39$, следовательно, $IMAGE25$ = $IMAGE42$; $IMAGE28$= $IMAGE44$.
Так как x, $IMAGE25$ – целые, x – по условию, а $IMAGE25$ – из-за нечётн. n, то g $IMAGE39$+ h $IMAGE39$= k $IMAGE39$, где k – целое.
Тройка решений g,h,k удовлетворяет уравнению Ферма, но все три числа меньше числа x первой тройки решений, потому что наибольшее число k из g,h,k меньше $IMAGE25$, так как $IMAGE25$=g $IMAGE52$, а $IMAGE25$<x, так как x=( $IMAGE25$) 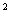 . Число k заведомо меньше числа z.
. Число k заведомо меньше числа z.
Повторим те же рассуждения для второй тройки решений g,h,k, начиная с (4):
(g $IMAGE15$) 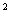 + (h $IMAGE15$)
+ (h $IMAGE15$) 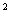 = (k $IMAGE15$)
= (k $IMAGE15$) 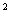 ; g = $IMAGE24$=( $IMAGE63$)
; g = $IMAGE24$=( $IMAGE63$) 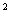 ; h = $IMAGE27$=( $IMAGE66$)
; h = $IMAGE27$=( $IMAGE66$) 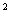 ; k = $IMAGE30$.
; k = $IMAGE30$.
$IMAGE63$ = $IMAGE34$= $IMAGE35$ и $IMAGE66$= $IMAGE37$= $IMAGE38$.
d = p $IMAGE39$; 2 c = q $IMAGE39$, следовательно, $IMAGE63$ = $IMAGE78$; $IMAGE66$= $IMAGE80$.
p $IMAGE39$+ q $IMAGE39$= r $IMAGE39$, где r – целое число. Все три числа p,q,r меньше числа $IMAGE63$ из второй тройки решений и r<k. Таким же образом получается 4-я тройка решений, 5-я и т.д. до $IMAGE85$.
При данных конечных целых положительных числах x,y,z не может существовать бес-конечной последовательности уменьшающихся целых положительных троек решений. Ряд натуральных чисел конечен. Отсюда целых положительных троек решений для целых положительных нечётных (и всех простых) значений показателя n (n>2) не существует.
Для чётных n=2m не кратных 4: (x 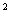 ) $IMAGE87$+(y
) $IMAGE87$+(y 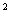 ) $IMAGE87$=(z
) $IMAGE87$=(z 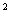 ) $IMAGE87$, m – нечётное. Если нет целых троек решений для показателя m, то их нет и для 2m (это показал Эйлер). Для n=4 и n=4k (k=1,2,3…) уже доказано, что целых положительных троек решений не существует.
) $IMAGE87$, m – нечётное. Если нет целых троек решений для показателя m, то их нет и для 2m (это показал Эйлер). Для n=4 и n=4k (k=1,2,3…) уже доказано, что целых положительных троек решений не существует.
А. Ф. Горбатов