База рефератов

Содержание

Введение. 2

1. Характеры.. 3

1.1 Определение характера. Основные свойства характеров. 3

1.2 Суммы характеров. Соотношение ортогональности. 6

1.3 Характеры Дирихле. 8

2. L-функция Дирихле. 13

3. Доказательство теоремы Дирихле. 29

Введение

Простые числа расположены в натуральном ряде весьма неравномерно.

Целью данной работы является доказательство следующей теоремы о простых числах в арифметической прогрессии.

Теорема Дирихле. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.

Пусть

mn + l, n=1,2, …,

прогрессия, удовлетворяющая условию теоремы.

Условие (m, l)=1, наложенные на числа m и e в формулировке теоремы, естественно, поскольку в случае, когда d=(m, l)>1, все члены прогрессии делятся на d и поэтому не являются простыми числами.

Сформулированная теория была впервые высказана Л. Эйлером в 1783 г. В 1798 г. А. Лежандр опубликовал доказательство для четных m, использовавшее, как выяснилось позднее, одну ошибочную лемму.

Полностью доказал теорему в 1837–1839 гг. Петер Густав Лежен-Дирихле (1805–1859), немецкий математик, автор трудов по аналитической теории чисел, теории функций, математической физике.

В 1837 г. вышли две работы Дирихле, посвященные теореме о простых числах в арифметической прогрессии. Они содержали формулировку теоремы в общем виде, однако доказательство приводилось только для случая, когда разность прогрессии есть простое число. В конце второй работы содержится построение характеров для произвольного модуля и некоторые утверждения о том, как можно доказать утверждение L (1,χ)¹0 для неглавных характеров x в одном случае. В 1839 г. Дилихле опубликовал полное доказательство теоремы о простых числах в арифметической прогрессии. С тех пор она носит его имя.

1. Характеры

1.1 Определение характера. Основные свойства характеров

Характером (от греческого хараæτήp-признак, особенность) χ конечной абелевой группы G называется не равная тождественно нулю комплекснозначная функция, определенная на этой группе и обладающая тем свойством, что если, АÎG и BÎG

χ (АВ)= χ (А) χ(В).

Обозначим через Е единичные элементы в группе G и через А^-1 обратный элемент для АÎG

Характеры группы G обладают следующими свойствами:

1. Если Е-единица группы, то для каждого характера χ

χ (Е)=1                          (1.1)

Доказательство. Пусть для каждого элемента АÎG справедливо неравенство

c₁(А)=c(АЕ)= c(А) χ (Е)

Из этого равенства получим, что c (Е)¹0. Теперь из равенства

c (Е)= c (ЕЕ)= c (Е) c (Е)=1

следует равенство (1.1)

2. c (А) ¹0 для каждого АÎG

Действительно, если бы χ (А) =0 для некоторого АÎG, то

c (А) χ (А^-1)= c (АА^-1)= χ (Е)=0,

а это противоречит свойству 1.

3. Если группа G имеет порядок h, то А^h=Е для каждого элемента АÎG Следовательно,

1= χ (Е)= χ (А^h)= χ (А)^h,

то есть χ (А) есть некоторый корень степени h из единицы.

Характер χ_1, обладающий свойством χ₁(А)=1 для каждого элемента АÎG, называется главным характером группы G. Остальные характеры называются неглавными.

Лемма 1. Пусть Н подгруппа конечной абелевой группы G, причем G/H – циклическая порядка n, тогда для каждого характера χ_H – подгруппы Н существует ровно n характеров.

Доказательство. Рассмотрим группу G= 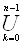g^kH, причем gⁿH=H, gⁿÎH и gⁿ=h₁=1.

Для каждого элемента XÎG существует и притом единственное к=к_х и h_х=h такое, что если 0£ к_х <n, то X= g^kх h_х=g^kh. Возьмем еще один элемент группы G, Y= g^m h_y, где 0£ m<n. Перемножим эти два элемента

ХY= g^к+m hh_y.

Определим характер χ (X).

χ (X)= χ (g^к h)= χ (g^к) χ (n)= χ ^к (g) χ _H (h).

В данном выражении неизвестным является χ (g).

χ ⁿ (g)= χ (gⁿ)= χ (h₁)= χ _H(h₁) – данное число.

χ (g)= – n корней из 1,

то есть ξ_јⁿ=χⁿ(g)= χ _H(h₁), получаем x^k (g)= ξ_јⁿ. Следовательно, x(g)= ξ₁, …, ξ_n

Из полученных равенств получаем:

χ (X)= χ ^k (g) χ _H(h_x)= ξ_j^kx χ _H (h_x)

χ (Y)= χ ^m (g) χ _H(h_y)= ξ_j^ky χ _H (h_y)

Определим умножение характеров

χ (X) χ (Y)= ξ_j^ky χ _H (h_y) ξ_j^k-x χ _H (h_x)= ξ_j^kx+ky χ _H (h_x) χ _H (h_y)= _j^k+m χ _H (hh_y)

Для того чтобы определение выполнялось, необходимо рассмотреть степень g^kx+kx. Возможны два случая:

1) Если 0£ к_х + k_y<n, то

к_х + k_y= k_xy,; h_xh_y = h_xy.

В этом случае определение выполняется.

2) Если n£ к_х + k_y<2n-1, то получим

к_х + k_y = n + k_xy..

Тогда

XY= g ^kx+ky h_xh_y=g^hg^kx+ky-n h_x h_y=g^kx+ky-n h₁h_xh_y

В свою очередь 0£ к_х + k_y – n£n-1 Þ k_x+k_y – n=k_xy, h₁h_xh_y = h_xy.

χ (XY) = ξ_j ^kх+kу χ_н (h_xу) = ξ_j ^{kх + kу – n} χ_н (h₁) χ_н(h_x) χ_н (h_y) = ξ_j^кх ξ_j ^ку ξ_j^{– n} χ_н (h₁) χ_н(h_x) χ_н (h_y) = ξ_j ^кх χ_н (h_1х) · ξ_j ^ку χ_н(h_y) = χ (X) χ(Y).

Лемма доказана.

5. Характеры конечной мультипликативной абелевой группы G образуют конечную мультипликативную абелевую группу Ĝ.

Под произведением двух характеров χ' и х χ'' группы G будем понимать характер х, определяемый следующим свойством:

χ (AB) = χ' (A) χ'' (В)

Для любого элемента АÎG, имеем:

χ (АВ) = χ' (АВ) χ'' (АВ) = χ' (А) χ' (В) · χ'' (А) χ'' (В) = χ(А) χ(В)

Таким образом, получаем χ ' χ '' действительно является характером.

Роль единичного элемента группы G играет главный характер χ₁

Обратным элементом G является:

χ₂ (g₁ g₂) = $IMAGE6$ = $IMAGE7$ $IMAGE8$= $IMAGE9$ = χ₂(g₁) χ₂(g₁)

1.2 Суммы характеров. Соотношение ортогональности

Пусть G – конечная мультипликативная абелева группа порядка h. Рассмотрим сумму:

S = $IMAGE10$,

где А пробегает все элементы G, и сумму

Т = $IMAGE11$

где c пробегает все элементы группы характеров Ĝ.

Рассмотрим чему равна каждая из сумм.

а) Если В-фиксированный элемент группы G и А пробегает все элементы G, то АВ также пробегает все элементы группы G. Следовательно,

S·c (В) = $IMAGE11$c (В) = $IMAGE13$ = $IMAGE10$ = S.

Получили Sc (В) = S, откуда следует, что (c (В) – 1)·S = 0. Следовательно, возможны два варианта:

1) S = 0, то c (В) – негативный характер

2) S≠0, то c (В) = 1 для каждого элемента В€G и в этом случае c (В)= c₁(В) есть главный характер и сумма S равна порядку h группы G. Таким образом,

S = $IMAGE10$ = { $IMAGE16$                                                  (1.2)

б) Если мы умножим сумму Т на некоторый характер c’ группы Ĝ, то аналогичным образом получим

c’ (А) Т = $IMAGE11$ c’ (А) = $IMAGE10$ = Т,

Следовательно,

1) или Т = 0, то А ≠Е

2) или Т ≠ 0, то c’ (А) = 1 для каждого характера c’€ G. В этом случае согласно свойству 3§ 1, имеем А=Е. И тогда Т=h. Таким образом,

Т = $IMAGE10$= { $IMAGE20$

1.3 Характеры Дирихле

Пусть m – положительное целое число. Определим числовые характеры по модулю m. Мы знаем, что j(m) приведенных классов вычетов по модулю m образуют мультипликативную абелеву группу порядка h=j(m). Мы можем, следовательно, рассмотреть характер этой группы. Но определение характера для приведенных классов вычета по модулю m можно перенести на множество целых чисел следующим образом. Положим

c(а)= c(А), если аÎА,

где А – приведенный класс вычетов по модулю m. Тогда очевидно, c(а)= c(b) (mod m), и c(ab)= c(а) c(b), если (а, m)=(b, m)=1. Поскольку c(А)¹0 для каждого приведенного класса вычетов А, то c(а)¹0, если (a, m)=1.

Это определение применимо только к целым числам а, которые взаимно просты с m.

Мы можем рассмотреть его на все целые числа, положив

c(а)=0, если (a, m)>1.

Следовательно, характер по модулю m есть арифметическая функция c, обладающая следующими свойствами:

c(а)= c(b), если с=b (mod m)

c(ab)= c(a) c(b) для всех целых a и b

c(а)=0, если (a, m)>1

c(а)¹0, если (a, m)=1

Имеется точно j(m) – количество характеров по модулю m, где j(m) – количество положительных целых чисел, не превосходящих m и взаимно простых с m. Они образуют мультипликативную абелеву группу приведенных классов вычета по mod m. Единичным элементом этой группы будет главный характер c_1, то есть такой характер, что c₁(а)=1, если (а, m)=1. Далее имеем следующее соотношение ортогональности:

$IMAGE21$= { $IMAGE22$

$IMAGE23$= { $IMAGE24$

Пусть m – положительное целое число. Определим числовые характеры по модулю m. Комплекснозначная функция, определенная для всех целых чисел n, называется числовым характером или характером Дирихле по модулю m, она удовлетворяет следующим условиям:

а) c (n) = 0 тогда и только тогда, когда (n, m) ≠ 1

б) c (n) периодична с периодом m

в) для любых чисел а и b

c (аb) = c (а) c (b)

Функция

c₁(n) = { $IMAGE25$

является числовым характером и называется главным характером. Остальные числовые характеры по модулю m называются неглавными.

Имеет место следующее утверждение о числовых характерах.

Теорема 1 Существует равно φ(m) числовых характеров по модулю m. Если c = c (n) – числовой характер по модулю m, то:

1) для n, взаимно простых с модулем m, значения c (n) есть корень из 1 степени φ(m).

2) для всех n выполняется неравенство /c (n)/ ≤1

3) Имеет место равенство

$IMAGE26${ $IMAGE27$

4) Для каждого целого числа n

$IMAGE28$ = { $IMAGE29$

Доказательство. Пусть c (n) – некоторый числовой характер по модулю m. Из