Министерство образования Российской Федерации

Башкирский государственный педагогический университет

Кафедра математического анализа

Дипломная квалификационная работа

Автор: Гарипов Ильгиз.

Тема: Свойства усредненной функции с сильной осцилляцией.

К защите допущен ____________

Заведующий кафедрой  к.ф. м. н. доцент Сафаров Т.Г.
Руководитель д.физ-мат. наук. профессор Султанаев Я.Т.

Уфа 2001

Содержание

                                                                                                                                    Стр.

 Введение                                                                                          3

§ 1 Свойства функции .                                                            4

§ 2 Свойства функции  и ее производных.                            5

2.1                                                                                 5

2.2                                                                                6

2.3  где a>0                                              7

2.4 $IMAGE6$                                                           9

§ 3 Поведение $IMAGE7$                                                                      11

3.1 $IMAGE8$                                                                               11

3.2                                                                                11

3.3 $IMAGE10$                                                            12

3.4 $IMAGE11$                                                                13

§ 4 Поведение $IMAGE12$                                                                      14

4.1 $IMAGE8$                                                                               14

4.2                                                                                15

4.3 $IMAGE10$                                                            15

4.4 $IMAGE11$                                                                16

Заключение                                                                                     17

Литература                                                                                     18

Введение

Пусть    произвольная  функция,  определенная  на  $IMAGE18$,  и  $IMAGE19$ при $IMAGE20$

Введем в рассмотрение функцию $IMAGE21$ с помощью следующего равенства:

$IMAGE22$                                   (1)

Назовем эту функцию усреднением функции  

Это название оправдано так как из (1) и теоремы о среднем для интегралов можем заключить

$IMAGE24$ $IMAGE24$ $IMAGE26$

$IMAGE27$

§  2 Свойства функции .

1.  Если $IMAGE29$, при $IMAGE30$, то $IMAGE31$ при $IMAGE30$
Доказательство:
  $IMAGE22$,  $IMAGE34$, $IMAGE30$  $IMAGE36$ " N >0, $IMAGE37$: $IMAGE38$  $IMAGE39$ 

2. $IMAGE40$                                        (2)

3. $IMAGE41$                 (3)

Дифференцируя формулу (1) по dx  получаем

$IMAGE42$                 (4)

$IMAGE43$(5)

§ 2 Свойства функции  и ее производных.

I) Рассмотрим вид функции  для случаев когда :

2.1  

$IMAGE48$

$IMAGE49$

2.2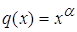 

 

$IMAGE51$

$IMAGE52$

$IMAGE53$

2.3 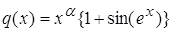 где a>0;

$IMAGE55$

$IMAGE56$

Разделим интеграл на два интеграла и вычислим их отдельно.

$IMAGE57$

Второй интеграл не оказывает влияния на первый, так как  при $IMAGE30$функция стремится к 0.

Доказательство:

$IMAGE59$

Рассматривая второй интеграл, мы получаем:

$IMAGE60$

Рассматривая первый интеграл, получаем:

$IMAGE61$

$IMAGE62$

Последние два слагаемых полученных при интегрировании содержат в произведении $IMAGE63$, то есть при возрастании x  эти слагаемые будут очень быстро уменьшатся и весь интеграл при $IMAGE30$ становится очень малым по сравнению с первой частью. Поэтому можно считать что при $IMAGE30$  $IMAGE66$

Следовательно:

  $IMAGE55$ $IMAGE36$

$IMAGE69$

2.4. $IMAGE6$

$IMAGE71$

Наложить на $IMAGE72$ ограничение, такое чтобы $IMAGE24$присутствие $IMAGE74$ не влияло на поведение функции.

$IMAGE75$

$IMAGE76$

Рассматривая полученное выражение можно заметить что

$IMAGE77$

становится пренебрежительно малым по отношению к остальной части

как только                    $IMAGE78$.                                                  Ограничение №1

В тоже время

$IMAGE79$

Становится бесконечно малым как только      $IMAGE80$.   Ограничение №2

Раскрывая в оставшейся части скобки, по Биному Ньютона получаем, что

$IMAGE81$

должен быть очень малым при $IMAGE30$то есть

$IMAGE83$ 

так как $IMAGE84$ ограниченная функция, к 0 должен стремится  $IMAGE85$.

$IMAGE86$  $IMAGE87$

$IMAGE88$

                                                         $IMAGE89$                         Ограничение №3

Учитывая ограничения 1, 2, 3 получаем:

$IMAGE90$

Следовательно, $IMAGE89$ ограничение на $IMAGE72$ удовлетворяющее поставленной задаче, при котором присутствие $IMAGE74$не влияет на поведение функции .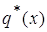

§ 3 Рассмотрим поведение  функции $IMAGE7$для случаев:

3.1) $IMAGE8$ 

$IMAGE97$

$IMAGE98$

$IMAGE99$

3.2)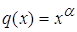  

$IMAGE101$

$IMAGE102$

$IMAGE103$

$IMAGE104$

3.3)    $IMAGE10$

$IMAGE106$

Вычислим отдельно интегральное выражение, стоящее в числителе:

$IMAGE107$=

$IMAGE108$=

$IMAGE24$  $IMAGE110$

$IMAGE24$ $IMAGE112$

$IMAGE24$ $IMAGE114$

$IMAGE115$

рассматривая пределы при $IMAGE116$ видим что на поведение функции оказывает влияние только главный член $IMAGE24$

$IMAGE118$

Поведение данной функции при $IMAGE116$ эквивалентно поведению функции

$IMAGE120$                                      (*)

Вычислим интеграл в знаменателе:

$IMAGE121$=

$IMAGE122$

$IMAGE123$

$IMAGE124$                                    (**)

Учитывая (*)и (**) получаем

$IMAGE125$

$IMAGE126$

Следовательно, по формуле (2) получаем $IMAGE127$

3.4   $IMAGE128$

  $IMAGE129$

Отдельно вычислим числитель и знаменатель:

$IMAGE130$

$IMAGE131$

По ранее доказанному в пункте 2.4 мы можем сказать что второй интеграл не оказывает влияния на поведение функции. Поэтому мы можем утверждать, что числитель эквивалентен выражению:

$IMAGE132$

$IMAGE133$

Вычислим знаменатель:

$IMAGE134$

Разделив интеграл на 2 интеграла, мы получаем:

$IMAGE135$

По пункту 2.4 можем вывести что второй интеграл не влияет на поведение функции при $IMAGE116$

 Следовательно, знаменатель:

$IMAGE137$

$IMAGE138$

$IMAGE139$

§4. Рассмотрим поведение второй производной $IMAGE140$

Для облегчения вычислений введем обозначения:

     $IMAGE141$

     $IMAGE142$

     $IMAGE143$

     $IMAGE144$

При этом формула для $IMAGE145$примет вид $IMAGE146$                              (6)

4.1 $IMAGE147$

$IMAGE148$

$IMAGE149$

$IMAGE150$

$IMAGE151$

$IMAGE152$

$IMAGE153$

$IMAGE154$

$IMAGE155$

$IMAGE156$

Виду того, что d(x) очень мал то $IMAGE157$ будет несравним с d(x) т.е.

$IMAGE158$

4.2 $IMAGE159$

$IMAGE160$

$IMAGE161$

$IMAGE162$

$IMAGE163$

$IMAGE164$

$IMAGE165$

используя равенства, полученные в пункте 2.2 и 3.2, преобразуя данное равенство, приходим к выражению:

$IMAGE166$

(Все выкладки приводить не буду в виду их громоздкости и сложности для восприятия. Добавлю только что все выкладки, примененные в данном пункте полностью повторяют ограничения и эквивалентные выражения, использованные в пунктах 2.2 и 3.2).

Отсюда следует что $IMAGE167$

4.3 $IMAGE168$

$IMAGE169$

$IMAGE170$

Используя данные, полученные в п.3.3 получаем что

$IMAGE171$

$IMAGE172$

Возвращаясь к п. 3.3 находим:

$IMAGE173$

$IMAGE174$

$IMAGE175$

Вычисляя $IMAGE145$по формуле 6, получаем:

$IMAGE177$

и $IMAGE167$

4.4 $IMAGE128$

$IMAGE180$

$IMAGE181$

$IMAGE182$

$IMAGE173$

$IMAGE184$

$IMAGE185$

$IMAGE177$

и $IMAGE167$

Заключение

В результате проведенного исследования поведения усредненной функции в случае осциллирующих коэфициентов, получены данные приведенные в следующей таблице:

$IMAGE188$	$IMAGE189$	$IMAGE190$	$IMAGE191$
$IMAGE192$	$IMAGE192$	$IMAGE192$	$IMAGE192$
$IMAGE196$	$IMAGE196$	$IMAGE198$	$IMAGE199$
$IMAGE200$	$IMAGE196$	$IMAGE198$	$IMAGE199$
$IMAGE204$	$IMAGE196$	$IMAGE198$	$IMAGE199$