Реферат:
«Сплайны. Финитные функции. Основные понятия, назначение. В сплайны Шенберга»
Введение
Функции, подобные тем, что сейчас называют сплайнами были известны математикам давно, начиная как минимум с Эйлера, но их интенсивное изучение началось, фактически, только в середине XX века. В 1946 году Исаак Шёнберг впервые употребил этот термин в качестве обозначения класса полиномиальных сплайнов. До 1960 годов сплайны были в основном инструментом теоретических исследований, они часто появлялись в качестве решений различных экстремальных и вариационных задач, особенно в теории приближений.
После 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании, что продолжается по сей день.
1. Сплайны
Под сплайном (от англ. spline – планка, рейка) обычно понимают кусочно-заданную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения.
Классический сплайн одной переменной строится так: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.
Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.
1.1 Кривые Безье
Кривые Безье́ или Кривые Бернштейна-Безье были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье и Полем де Кастельжо.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Определение
Кривая Безье – параметрическая кривая, задаваемая выражением:
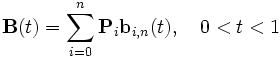(1.1)
где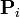 
– функция компонент векторов опорных вершин, а 
– базисные функции кривой Безье, называемые также полиномами Бернштейна.
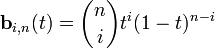(1.2)
, (1.3)
где n – степень полинома, i – порядковый номер опорной вершины
1.2 Виды кривых Безье:
1. Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
$IMAGE6$ (1.4)
2. Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2:
$IMAGE7$ (1.5)
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах.
3. Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
$IMAGE8$ (1.6)
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.
$IMAGE9$
Рисунок 1 Кубическая кривая Безье
В матричной форме кубическая кривая Безье записывается следующим образом:
$IMAGE10$, (1.7)
где $IMAGE11$ называется базисной матрицей Безье:
$IMAGE12$ (1.8)
В современных графических системах, таких как PostScript, Metafont и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
1.3 Построение кривых Безье
1. Линейные кривые
Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
$IMAGE13$
Рисунок 2 Построение линейной кривой Безье
2. Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:
Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
$IMAGE14$
Рисунок 3 Построение квадратичной кривой Безье
3. Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
$IMAGE15$
Рисунок 4 Построение кубической кривой Безье
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
$IMAGE16$
Рисунок 5 Построение кривой Безье 4-ой степени
1.4 Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой.
1.5 Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами $IMAGE17$ преобразовывается в кубическую кривую Безье с координатами:
$IMAGE18$
2. Финитные функции
Финитной называется функция $IMAGE19$, определенная для всех $IMAGE20$, но отличная от нуля лишь на некоторой конечной области $IMAGE21$, называемой конечным носителем:
$IMAGE22$ (2.1)
Для $IMAGE23$, определенных на $IMAGE21$, построение базиса $IMAGE25$ из финитных функций осуществляется следующим образом. Сначала область $IMAGE21$, в которой решается задача, некоторым регулярным образом покрывается конечным числом $IMAGE27$ перекрывающихся подобластей $IMAGE28$, например как на рис. 6.1:
$IMAGE29$ (2.2)
Желательно, чтобы $IMAGE30$ только для $IMAGE31$, смежных с $IMAGE28$.
Подобласти $IMAGE28$ получили название конечные элементы.
Затем на каждом $IMAGE28$ как на конечном носителе строим базисную финитную функцию $IMAGE35$. Все функции таким образом выбранного базиса линейно независимы в силу условий (2.1), (2.2).
Отметим преимущества такого выбора базиса:
а) ввиду того, что $IMAGE28$ выбираются значительно меньшими $IMAGE21$ и при этом скалярные произведения
$IMAGE38$ (2.3)
равны нулю для функций с непересекающимися носителями, матрица проекционного уравнения будет сильно разрежена. Более того, если условие $IMAGE30$ выполняется только для смежных носителей, то матрица получается ленточной, т.е. аналогична той, к которой приводят сеточные методы;
б) возможность выбора специфических приграничных конечных элементов и связанных с ними финитных функций, учитывающих особенности границы, позволяет эффективно решать краевые задачи на достаточно произвольной области $IMAGE21$.
Основная трудность аппроксимации финитными функциями состоит в сопряжении финитных функций на границах Wk таким образом, чтобы функция $IMAGE41$ в целом была непрерывна вместе со своими производными достаточно высокого порядка.
При таком выборе базиса естественно поставить вопросы о его полноте, выборе вида функций $IMAGE35$ и аппроксимационных свойствах разложения искомого решения
$IMAGE43$. (2.4)
На все эти вопросы частично дает ответ теория Стренга-Фикса.
Изложим основные идеи этой теории для функций одной переменной с регулярными конечными элементами.
Область $IMAGE44$ покрываем равномерной сеткой
$IMAGE45$, [p] – целая часть p.
Конечные элементы $IMAGE28$ выберем как отрезки длиной $IMAGE47$ с центром в точке $IMAGE48$: $IMAGE49$. Если $IMAGE50$, смежные элементы не пересекаются и их длина равна $IMAGE51$: если $IMAGE52$, то длина пересечения равна $IMAGE51$, длина $IMAGE28$ равна $IMAGE55$; при $IMAGE56$ – длина пересечения $IMAGE55$, длина $IMAGE28$ равна $IMAGE59$. Заметим, что такое покрытие полностью удовлетворяет условиям (2.2). Все базисные финитные функции с носителями $IMAGE28$ выберем одинаковой формы как сдвиги одной «стандартной» финитной функции $IMAGE61$:
$IMAGE62$; $IMAGE63$ (2.5)
Если «стандартная» функция нормирована к единице, то ее сдвиги записываются в виде
$IMAGE64$ (2.6)
Теорема Стренга-Фикса (один из вариантов)
Допустим, что $IMAGE65$. В этом случае для $IMAGE66$ существует преобразование Фурье:
прямое $IMAGE67$ обратное $IMAGE68$
Допустим, что для преобразования Фурье стандартной финитной функции $IMAGE66$ выполнено условие
$IMAGE70$ и $IMAGE71$ при $IMAGE72$ (2.7)
(т.е. в $IMAGE73$точках $IMAGE74$ имеет нули $IMAGE75$й кратности).
Тогда существуют такие $IMAGE76$, что при $IMAGE77$
$IMAGE78$.
Это значит, что если, например, подобрать $IMAGE79$, у которой условия теоремы выполняются для $IMAGE80$, то аппроксимация самой функции $IMAGE23$ имеет порядок $IMAGE82$, аппроксимация ее первой производной $IMAGE83$, второй – $IMAGE84$.
Наличие такой центральной теоремы, а также еще ряда доказанных Стренгом-Фиксом теорем, в частности о существовании функций, удовлетворяющих условиям (2.7), дает алгоритм для построения базисных финитных функций, обладающих необходимыми аппроксимационными свойствами.
3. B-сплайны Шёнберга
В вычислительной математике B-сплайном называют сплайн-функцию, имеющую наименьший носитель для заданной степени, порядка гладкости и разбиения области определения. Фундаментальная теорема устанавливает, что любая сплайн-функция для заданной степени, гладкости и области определения может быть представлена как линейная комбинация B-сплайнов той же степени и гладкости на той же области определения. [1] Термин B-сплайн был введён И. Шёнбергом и является сокращением от словосочетания «базисный сплайн». [2] B-сплайны могут быть вычислены с помощью алгоритма де Бора, обладающего устойчивостью.
В системах автоматизированного проектирования и компьютерной графике термин B-сплайн часто описывает сплайн-кривую, которая задана сплайн-функциями, выраженными линейными комбинациями B-сплайнов.
Когда узлы равноудалены друг от друга, говорят, что B-сплайн является однородным, в противном случае его называют неоднородным.
Когда количество узлов совпадает со степенью сплайна, B-сплайн вырождается в кривую Безье. Форма базисной функции определяется расположением узлов. Масштабирование или параллельный перенос базисного вектора не влияет на базисную функцию.
Сплайн содержится в выпуклой оболочке его опорных точек.
Базисный сплайн степени n: $IMAGE85$.
не обращается в нуль только на промежутке [ti, ti+n+1], то есть:
$IMAGE86$.