Министерство общего и профессионального образования РФ.
Уральский государственный университет.
Сетевые графики
Курсовая работа студента
группы ИС-202 Лисицын В.С.
Руководитель Замятин А. П.
Екатеринбург, 1999.
Многие крупные проекты, такие как строительство дома, изготовление станка, разработка автоматизированной системы бухгалтерского учета и т.д., можно разбить на большое количество различных операций (работ). Некоторые из этих операций могут выполняться одновременно, другие — только последовательно: одна операция после окончания другой. Например, при строительстве дома можно совместить во времени внутренние отделочные работы и работы по благоустройству территории, однако возводить стены можно только после того, как будет готов фундамент.
Задачи планирования работ по осуществлению некоторого проекта состоят в определении времени возможного окончания как всего проекта в целом, так и отдельных работ, образующих проект; в определении резервов времени для выполнения отдельных работ; в определении критических работ, то есть таких работ, задержка в выполнении которых ведет к задержке выполнения всего проекта в целом; в управлении ресурсами, если таковые имеются и т.п.
Пусть некоторый проект W состоит из работ V1,...,Vn; для каждой работы Vk, известно, или может быть достаточно точно оценено время ее выполнения t(Vk). Кроме того, для каждой работы Vk известен, возможно пустой, список ПРЕДШ(Vk) работ, непосредственно предшествующих выполнению работы Vk. Иначе говоря, работа Vk может начать выполняться только после завершения всех работ, входящих в список ПРЕДШ(Vk).
Для удобства, в список работ проекта W добавим две фиктивные работы s и p, где работа s обозначает начало всего проекта W. а работа p — завершение работ по проекту W. При этом будем считать, что работа s предшествует всем тем работам vÎW, для которых список ПРЕДШ(v) пуст, иначе говоря, для всех таких работ vÎW положим ПРЕДШ(v)={s}. Положим далее ПРЕДШ(s) =Æ, ПРЕДШ(p)={vÎW: v не входит ни в один список ПРЕДШ(w)}, то есть считаем, что работе p предшествуют все те работы, которые могут выполняться самыми последними. Время выполнения работ s и p естественно положить равными нулю: t(s)=t(p)=0.
Весь проект W теперь удобно представить в виде сети G=(V,E,c). Ориентированный взвешенный граф G=(V,E,c) называется сетью. Сеть может быть представлена матрицей весов дуг, массивами смежностей СЛЕД или ПРЕДШ, или списками СЛЕД[v] или ПРЕДШ[v]. При этом записи в списках смежности состоят из трех компонент: поля имени узла, поля веса соответствующей дуги и поля ссылки на следующую запись), где сеть G=(V,E,c) определим по правилам:
1. V=W, то есть множеством узлов объявим множество работ;
2. E={(v,w) : vÎПРЕДШ(w)}, то есть отношение предшествования задает дуги в сети;
3. c(v,w)=t(w).
Так построенную сеть G часто называют сетевым графиком выполнения работ по проекту W. Легко видеть, что списки смежностей этой сети ПРЕДШ[v] совпадают с заданными для проекта списками предшествующих работ ПРЕДШ(v).
Понятно, что сетевой график любого проекта не должен содержать контуров. Действительно, пусть узлы Vk1,Vk2,...,Vkr=Vk1 образуют контур в сети G. Это означает, что работа Vk2 не может начаться раньше, чем будет завершена работа Vk1, работа Vk3 — раньше, чем завершится работа Vk2, и т.д., и, наконец, Vkr = Vk1 — раньше, чем будет завершена работа Vkr-1. Но тогда никакая из работ Vk1,...,Vkr никогда не сможет быть выполнена. А каждый реальный проект должен допускать возможность его завершения. Следовательно, в сетевом графике нет контуров.
Отсутствие контуров в сети G позволяет пронумеровать работы проекта W таким образом, чтобы для каждой дуги (Vi,Vj) сети G выполнялось условие i<j, то есть каждая дуга идёт из узла с меньшим номером в узел с большим номером. Осуществить такую нумерацию узлов сети G можно с помощью алгоритма топологической сортировки. Поэтому в дальнейшем будем считать, что узлы в сети G топологически отсортированы.
Конечной целью построения сетевой модели является получение информации о возможных сроках выполнения как отдельных работ, так и о возможном сроке выполнения всего проекта в целом. Обозначим через PBЫП(v) (соответственно PHAЧ(v)) наиболее ранний возможный срок выполнения работы v (соответственно наиболее ранний возможный срок начала работы v). Удобно считать, что PBЫП(s)=PHAЧ(s)=0. Поскольку начать выполнять работу v можно только после того, как будут выполнены все работы, предшествующие данной работе v, то получим следующие формулы для расчета значений PHAЧ(v) и PBЫП(w):
PHAЧ(v) = МАКС{PBЫП(w): wÎПРЕДШ(v)},
PBЫП(v)= PHAЧ(v) + t(v).
Значение PBЫП(p) дает наиболее ранний возможный срок завершения всего проекта в целом. Приведем запись алгоритма, непосредственно вычисляющего характеристики РНАЧ и РВЫП.
АЛГОРИТМ 1.
Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), vÎV.
Результаты: Наиболее ранние возможные сроки начала и выполнения работ РНАЧ(v), РВЫП(v), vÎV.
Шаг 1. Объявить возможные ранние сроки начала РНАЧ(v) и выполнения РВЫП(v) работ равными нулю. Текущей вершиной объявить первую вершину vk=v1.
Шаг 2. Всем вершинам v предшествующим текущей вершине vk, значение РНАЧ(vk) присвоить максимум из значений РВЫП(v) и РНАЧ(vk). Значение РВЫП(vk) положить равным значению РНАЧ(vk) плюс время выполнения самой работы текущей вершины t(vk).
Шаг 3. Если имеется следующая вершина (работа) после текущей, то объявить ее текущей вершиной vk, иначе перейти в Шаг 5.
Шаг 4. Вернуться в Шаг 2.
Шаг 5. Выдать наиболее ранние возможные сроки начала и выполнения работ РНАЧ(v), РВЫП(v), vÎV, конец работы алгоритма.
Пусть T — плановый срок выполнения проекта W. Ясно, что Т должно удовлетворять неравенству Т >= РВЫП(Vn+1).
Через ПВЫП(v) (соответственно ПНАЧ(v)) обозначим наиболее поздний допустимый срок выполнения (начала) работы v, то есть такой срок, который не увеличивает срок Т реализации всего проекта.
Значения возможных и допустимых сроков выполнения работ позволяют определить резервы времени для выполнения той или иной работы. Полный резерв (иногда его называют суммарный) времени выполнения работ определяется по формуле:
PE3EPB(v)=ПHAЧ(v)-PHAЧ(v).
Значение PE3EPB(v) равно максимальной задержке в выполнении работы v, не влияющей на плановый срок Т. Понятно, что справедливо и такое равенство: РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).
Работы, имеющие нулевой резерв времени, называются критическими. Через любую такую работу проходит некоторый максимальный s-p-путь в сети G. Критические работы характеризуются тем, что любая задержка в их выполнении автоматически ведет к увеличению времени выполнения всего проекта.
Приведем запись алгоритма, непосредственно вычисляющего характеристики ПВЫП и ПНАЧ.
АЛГОРИТМ 2.
Данные: Сетевой график G работ V, заданный списками ПРЕДШ(v), vÎV, плановый срок окончания проекта – Т.
Результаты: Наиболее поздние допустимые сроки выполнения и начала работ ПВЫП(v) и ПНАЧ(v).
Шаг 1. Объявить для всех работ vÎV значение наиболее позднего срока выполнения работ равным Т – значению планового срока окончание проекта и вершину vp фиктивной работы p объявить текущей vk.
Шаг 2. Присвоить значение ПНАЧ текущей работы vk равным значению ПВЫП работы и вычесть время выполнения текущей работы.
Шаг 3. Присвоить значению ПВЫП(v) для всех работ vÎПРЕДШ(v) предшествующих текущей работе vk минимальное значение из значений ПВЫП выполнения роботы v или ПНАЧ выполнения текущей работы vk, если таковых нет перейти в Шаг 4.
Шаг 4. Если имеется предыдущая вершина (работа) к текущей, то объявить её текущей, иначе перейти в Шаг 6.
Шаг 5. Перейти в Шаг 2.
Шаг 6. Выдать наиболее поздние допустимые сроки выполнения и начала работ ПВЫП(v) и ПНАЧ(v), конец работы алгоритма.
Проиллюстрируем работу приведенных алгоритмов на следующих примерах:
Пример 1: Проект гаража для стоянки автопогрузчиков.
| n | Наименование работы | Предшеству-ющие работы | Время вы-полнения t(vk) |
| 1 | Начало проекта (фиктивн. работа) | Нет | 0 |
| 2 | Срезка растительного слоя грунта | 1 | 5 |
| 3 | Монтаж каркаса | 2 | 30 |
| 4 | Обшивка стен профнастилом | 3 | 15 |
| 5 | Кровля из профнастила | 3 | 12 |
| 6 | Заполнение проема воротами | 4 | 5 |
| 7 | Масляная окраска ворот и профнастила | 5,6 | 10 |
| 8 | Щебёночное основание под полы | 7 | 3 |
| 9 | Асфальтовое покрытие | 8 | 3 |
| 10 | Уборка строительного мусора после строит. | 7 | 3 |
| 11 | Конец проекта (фиктивная работа) | 9,10 | 0 |
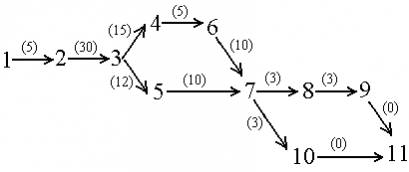
Рис 1. Проект гаража для стоянки автопогрузчиков.
Найдем значения наиболее раннего начала и выполнения работ проекта посредством алгоритма 1. Работу алгоритма изложим в виде последовательности выполняемых шагов.
| Шаг n | Действия выполняемые шагом |
| 1 | Объявление значений РНАЧ(v) и РВЫП(v), vÎV равными нулю. Текущая вершина vk=1. |
| 2 | Вершин предшествующей первой нет. РВЫП(1)=РНАЧ(1)+t(1). {РНАЧ(1) стало равным 0} |
| 3 | Текущая вершина vk=2. |
| 4 | Переход в Шаг 2. |
| 2 | РНАЧ(2)=МАКС{РВЫП(1),РНАЧ(2)} {РНАЧ(2) стало равным 0} РВЫП(2)=РНАЧ(2)+t(2) {РВЫП(2) стало равным 5}. |
| 3 | Текущая вершина vk=3. |
| 4 | Переход в Шаг 2. |
| 2 | РНАЧ(3)=МАКС{РВЫП(2),РНАЧ(3)} {РНАЧ(3) стало равным 5} РВЫП(3)=РНАЧ(3)+t(3) {РВЫП(3) стало равным 35}. |
| 3 | Текущая вершина vk=4. |
| 4 | Переход в Шаг 2. |
| 2 | РНАЧ(4)=МАКС{РВЫП(3),РНАЧ(4)}{РНАЧ(4) стало равным 35} РВЫП(4)=РНАЧ(4)+t(4) {РВЫП(4) стало равным 50}. |
| 3 | Текущая вершина vk=5. |
| 4 | Переход в Шаг 2. |
| 2 | РНАЧ(5)=МАКС{РВЫП(3),РНАЧ(5)}{РНАЧ(5) стало равным 35} РВЫП(5)=РНАЧ(5)+t(5) {РВЫП(5) стало равным 47}. |
| 3 | Текущая вершина vk=6. |
| 4 | Переход в Шаг 2. |
| 2 | РНАЧ(6)=МАКС{РВЫП(4),РНАЧ(6)}{РНАЧ(6) стало равным 50} РВЫП(6)=РНАЧ(6)+t(6) {РВЫП(6) стало равным 55}. |
| 3 | Текущая вершина vk=7. |
| 4 | Переход в Шаг 2. |
| 2 | РНА |
|
|
|
|