Разностные схемы для уравнений параболического типа
Рассмотрим задачу Коши для уравнения теплопроводности
, 
, 
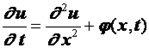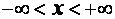, (3.5)
с условием на прямой t=0
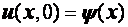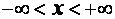, . (3.6)
Требуется найти функцию $IMAGE7$, которая при и 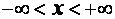удовлетворяла бы уравнению (3.5), а при $IMAGE10$ выполняла бы условие (3.6).
Будем считать, что задача (3.5), (3.6) имеет в верхней полуплоскости единственное решение $IMAGE7$, непрерывное вместе со своими производными
$IMAGE12$, i=1, 2 и $IMAGE13$, k=1, 2, 3, 4.
Запишем задачу (3.5), (3.6) в виде $IMAGE14$. Для этого достаточно положить
$IMAGE15$
$IMAGE16$
Будем далее считать, что t изменяется в пределах $IMAGE17$. В рассматриваемом случае
$IMAGE18$,
Г − объединение прямых t=0 и t=T.
Выберем прямоугольную сетку и заменим область $IMAGE19$ сеточной областью $IMAGE20$. К области $IMAGE20$ отнесем совокупность узлов $IMAGE22$, где
$IMAGE23$, $IMAGE24$, $IMAGE25$,
$IMAGE26$, $IMAGE27$, $IMAGE28$, $IMAGE29$.
Заменим задачу $IMAGE14$ разностной схемой вида $IMAGE31$. Обозначим через $IMAGE32$ точное значение решения задачи $IMAGE14$ в узле $IMAGE34$, а через $IMAGE35$ – соответствующее приближенное решение. Имеем
$IMAGE36$
$IMAGE37$
Для замены выражений $IMAGE38$и $IMAGE39$воспользуемся формулами численного дифференцирования. Имеем:
$IMAGE40$, (3.7)
$IMAGE41$, (3.8)
$IMAGE42$, (3.9)
$IMAGE43$ (3.10)
Назовем некоторую совокупность узлов, привлекаемых для замены задачи $IMAGE14$ в узле $IMAGE34$, разностной схемой $IMAGE31$, шаблоном. Наиболее употребительные шаблоны изображены на рис. 3:
$IMAGE47$
$IMAGE48$
Рис. 3. Явный и неявный шаблоны
Рассмотрим явный двухслойный шаблон. Для него
$IMAGE49$(3.11)
Здесь мы воспользовались формулами (3.7) и (3.10) и обозначили
$IMAGE50$.
Введем обозначение
$IMAGE51$ (3.12)
Теперь на основании формул (3.11), (3.12) можно записать разностную схему для задачи $IMAGE14$:
$IMAGE53$, (3.13)
где разностный оператор $IMAGE54$определяется по правилу
$IMAGE55$
Аналогично, если использовать неявный двухслойный шаблон, можно получить такую разностную схему:
$IMAGE56$, (3.14)
где
$IMAGE57$
$IMAGE51$
На основании формул (3.11) и (3.13) можно записать
$IMAGE59$,
где $IMAGE60$
Аналогично, используя (3.11), (3.10), (3.14), получим
$IMAGE61$,
$IMAGE62$.
Выясним порядок аппроксимации разностных схем (3.13) и (3.14). В качестве $IMAGE63$ возьмем линейное множество всех пар ограниченных функций
$IMAGE64$.
Норму в $IMAGE63$ определим правилом
$IMAGE66$
Пусть $IMAGE67$, где r и s – некоторые положительные числа.
Предположим, что для $IMAGE68$ и $IMAGE69$ верны оценки
$IMAGE70$, $IMAGE71$.
Тогда легко получить
$IMAGE72$, (3.15)
$IMAGE73$. (3.16)
Для параболических уравнений, как мы увидим далее, в случае схемы (3.13) можно взять S=2, а в случае схемы (3.14) можно взять S=1.
Из формул (3.15), (3.16) следует, что разностные схемы (3.13), (3.14) аппроксимируют задачу $IMAGE14$ с погрешностью порядка S относительно h.
Разностная схема (3.13) позволяет по значениям решения на нулевом слое, то есть по значениям $IMAGE75$ вычислить значения на первом слое $IMAGE76$ . Для этого достаточно в (3.13) положить n = 0 и произвести вычисления, носящие рекурсионный характер. Потом по значениям $IMAGE77$ можно аналогично при n = 1 вычислить значения $IMAGE78$ и т.д. В силу этого разностную схему (3.13) называют явной.
Разностная схема (3.14) такими свойствами не обладает. Действительно, если мы в (3.14) положим n = 0, то в левой части полученной формулы будет линейная комбинация из значений $IMAGE79$, в правой части будут значения известной функции $IMAGE80$ и $IMAGE81$. Для вычисления значений на первом слое $IMAGE82$ в этом случае необходимо решать бесконечную систему линейных уравнений. По этой причине схему (3.14) называют неявной.
Определим норму в пространстве $IMAGE83$ по правилу
$IMAGE84$.
Рассмотрим явную разностную схему (3.13). Выясним, при каких значениях r, $IMAGE85$ возможна устойчивость этой схемы.
Для доказательства устойчивости надо показать, что разностная схема однозначно разрешима и при любых
$IMAGE64$, $IMAGE87$
имеет место оценка $IMAGE88$,
где М – постоянная, не зависящая от $IMAGE89$ и $IMAGE90$ и $IMAGE91$.
Разностная схема (3.13) – явная, и поэтому ее однозначная разрешимость очевидна.
Перепишем формулу $IMAGE91$ в виде
$IMAGE93$, $IMAGE94$, (3.17)
$IMAGE95$.
Пусть выполнено условие
$IMAGE96$ или $IMAGE97$. (3.18)
Тогда из (3.17) получим:
$IMAGE98$,
или
$IMAGE99$. (3.19)
Неравенство (3.19) означает, что при $IMAGE100$, $IMAGE101$ не превосходит $IMAGE102$, то есть $IMAGE102$ не возрастает с увеличением n.
Это свойство однородной разностной схемы принято называть принципом максимума. Положим в (3.19) $IMAGE104$. Это даст
$IMAGE105$,
$IMAGE106$,
$IMAGE107$.
Заметим, что $IMAGE108$ есть число, независящее от m и n. Просуммировав последние неравенства и, учитывая, что $IMAGE94$, получим
$IMAGE110$ (3.20)
где обозначено
$IMAGE111$
На основании (3.20) можно записать
$IMAGE112$ или $IMAGE88$.
Таким образом, разностная схема (3.13) при выполнении условия (3.18), налагаемого на $IMAGE114$ и h, устойчива. Условие (3.18) весьма жестко, ибо из него следует, что
$IMAGE115$. (3.21)
Это приводит к тому, что если мы желаем сохранить устойчивость, то при вычислениях по схеме (3.13) шаг по времени $IMAGE114$ приходится выбирать очень малым.
Обратимся теперь к разностной схеме (3.14), соответствующей шаблону, изображенному на рис. 4,
$IMAGE117$
Рис. 4. Неявный двухслойный шаблон
и перепишем ее в виде
$IMAGE118$ (3.22)
Посмотрим, какие надо проделать вычисления, чтобы, используя формулы (3.22), можно было вычислить, например, значения $IMAGE77$ на первом временном слое со значениями $IMAGE120$ на нулевом временном слое. Положив в формулах (3.22) n=0, получим:
$IMAGE121$ (3.23)
Формулы (3.23) представляют собой бесконечную систему линейных уравнений относительно неизвестных $IMAGE122$ .
Решение таких систем является сложной и трудоемкой задачей, поэтому разностные схемы (3.14) неудобны для задач Коши на бесконечных отрезках и применяется редко. Однако если отрезок оси x, на котором рассматривается задача Коши, конечен, то есть $IMAGE123$, а на прямых x=a и x=b дополнительно заданы некоторые ограничения на решение $IMAGE7$, то разностные схемы вида (3.14) оказываются весьма эффективными. В частности, можно показать, что такие схемы являются абсолютно устойчивыми, то есть устойчивыми при любых значениях $IMAGE125$.
Если, например, на отрезках прямых x=a и x=b, заданы условия $IMAGE126$, $IMAGE127$, то вид системы (3.23) существенно изменится:
$IMAGE129$ (3.24)
Формулы (3.24) представляют собой систему M+1 алгебраических уравнений относительно $IMAGE130$. Матрица этой системы трехдиагональна и ее можно решить методом прогонки. Отсюда ясно, что реализация неявных разностных схем требует больших вычислительных затрат для вычисления решения на одном временном слое, но таких слоев может быть немного из-за того, что в этом случае отсутствуют ограничения на соотношение $IMAGE131$. Если пользоваться явной разностной схемой, то вычисление решения на следующем слое осуществляется по рекурсионному правилу и связано с минимальными вычислительными затратами, однако из-за ограничения
$IMAGE132$
число временных слоев в случае явных схем может быть существенно большим по сравнению с числом временных слоев для неявных схем.
Рассмотрим теперь вопрос о сходимости схемы (3.13). Эта схема аппроксимирует задачу (3.5), (3.6) с погрешностью порядка $IMAGE133$ и устойчива при $IMAGE134$. Поэтому схема (3.13), по теореме об аппроксимации и устойчивости, будет сходящейся. При этом погрешность для приближенного решения будет величиной порядка $IMAGE133$.