Отдел образования администрации Центрального района
Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 4
Секция математика
НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
По теме
Разбиение натурального ряда
Сорока Александра Александровна
Василькова Евгения Сергеевна
Учащихся 11 В класса МОУ СОШ №4
Центрального района
8-905-958-2583
8-913-954-3357
Руководитель: Тропина Наталья
Валерьяновна,
Кандидат педагогических наук
доцент кафедры математического анализа
НГПУ
(работа выполнена в МОУ СОШ №4)
Новосибирск 2008г.
Содержание
Введение
§1. Основные понятия и определения
§2. Две последовательности. Их свойства
§3. Упражнения
§4. Геометрическая интерпретация
§5. Некоторые приложения (Палиндромы)
Заключение
Список литературы
рациональный иррациональный число
ВВЕДЕНИЕ
Целью данной работы является изучение вопроса о разбиениях натурального ряда на две непересекающиеся возрастающие последовательности.
Работа состоит из пяти параграфов:
Первый параграф посвящен понятиям и определениям, которые пригодятся нам в работе.
Во втором параграфе идет речь о построении двух последовательностей и о гипотезе Акулича.
В третьем параграфе приведены упражнения.
Четвертый параграф посвящен геометрической интерпретации построения последовательностей.
В пятом параграфе приведены некоторые приложения.
§1 Основные понятия и определения
Целая и дробная части числа
Определение 1. Целой частью числа x называется наибольшее целое число r, не превышающее x.
Целая часть числа x обозначается символом [x] или (реже) E(x) (от фр. entier "антье" — целый).
Если x принадлежит промежутку
[r; r +1),
где r — целое число, то [x]=r, т.е. x находится на промежутке [ [x]; [x]+1). По свойствам числовых неравенств, разность x-[x] будет на промежутке [0; 1).
Определение 2. Число q = x - [x] называют дробной частью числа x и обозначают {x}. Следовательно, дробная часть числа всегда неотрицательна и не превышает 1, тогда как целая часть числа может принимать как положительные значения, так и неположительные. Таким образом {x} = x - [x], а, следовательно, x = [x] + {x}.
Примеры
| [5]=5 | [7,2]=7 | [-3]=-3 | [-4,2]=-5 | [0]=0 |
| {5}=0 | {7,2}=0,2 | {-3}=0 | {-4,2}=0,8 | {0}= |
Свойство целой части
[x+n] = [x]+n
где n – натуральное число
Рациональные и иррациональные числа и их свойства
Определение 3.Рациональным числом называется число, которое можно представить в виде дроби
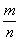
где m – целое число, а n – натуральное.
Определение 4. Если число не представимо в виде 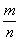, то такое число называется иррациональным.
Теорема 1. Любое рациональное число представимо в виде конечной или бесконечной периодической дроби.
Любое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.
Примеры
0,5=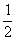 
-рациональное число
0,(3)=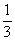 
- рациональное число
1,0123456789101112…-иррациональное число
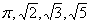- иррациональное число
Свойства арифметических действий над рациональными и иррациональными числами
1. Если $IMAGE6$- рациональные числа, то $IMAGE7$, $IMAGE8$, $IMAGE9$, $IMAGE10$, $IMAGE11$ - рациональные числа.
Дано: Доказательство
$IMAGE12$ ; $IMAGE13$ $IMAGE14$ - рациональное
2. Если r-рациональное число, $IMAGE15$-иррациональное число, то
$IMAGE16$ - иррациональные числа.
Доказательство: (от противного)
Предположим что
$IMAGE17$но $IMAGE18$- противоречие
3. Если $IMAGE19$,то про $IMAGE20$ ничего определенного нельзя сказать.
Примеры
$IMAGE21$
§2 Две последовательности. Их свойства
В этом параграфе речь пойдет о задачах, посвященных разбиению натурального ряда на последовательности и о теореме, доказывающей их.
Рассмотрим один из способов разбиения натурального ряда на две возрастающие непересекающиеся последовательности
$IMAGE22$ и $IMAGE23$
которые при любом натуральном n удовлетворяют условию $IMAGE24$.
Двигаясь по натуральному ряду, можем последовательно вычислять члены обеих последовательностей.
$IMAGE25$
Поскольку все $IMAGE26$, то наименьшее натуральное число, т.е. 1- должно равняться $IMAGE27$.
Следовательно
$IMAGE28$
и так далее. Каждый раз, выбирая наименьшее неиспользованное натуральное число и считая его равным $IMAGE29$, затем, находя $IMAGE30$по формуле
$IMAGE24$
можем строить последовательности.
В 1877 году в «Теории звука» лорд Рэлей писал: «если x есть некоторое положительное иррациональное число, меньшее единицы, то можно взять два ряда величин n/x и n/(x-1) где n = 1,2,3…; каждое число, принадлежащее к тому или иному ряду, и только оно одно, будет заключено между двумя последовательными натуральными числами”. Т.е.
$IMAGE32$ и $IMAGE33$
заполняют без пропусков и перекрытий весь натуральный ряд, если
0<x<1 и x $IMAGE34$Q
Гипотеза Акулича и явные формулы
И.Ф. Акулич предложил гипотезу: отношение количества a-чисел к количеству b-чисел стремится к «золотому сечению»
$IMAGE35$
(где a-числа – числа, принадлежащие последовательности $IMAGE36$, b-числа- числа, принадлежащие последовательности $IMAGE37$).
$IMAGE38$[(1+ $IMAGE39$)n/2]
$IMAGE40$=[(1+ $IMAGE41$)n/2]+n=[(3+ $IMAGE41$)n/2]
Выведем из явных формул гипотезу Акулича.
Обозначим
$IMAGE43$ ; $IMAGE44$
Рассмотрим натуральное число N и выясним сколько a-чисел и b-чисел среди первых N натуральных чисел, если последовательности заданы формулами:
$IMAGE38$ $IMAGE46$ ; $IMAGE47$
Неравенства $IMAGE48$равносильно, по определению целой части, неравенству $IMAGE49$<N+1, т.е. неравенству n<(N+1)/ $IMAGE15$. Значит, a-чисел среди первых N натуральных чисел имеется ровно [(N+1)/ $IMAGE15$]. Аналогично, b-чисел
[(N+1)/ $IMAGE52$]
Тогда отношение количества a - чисел к количеству b- чисел равно
$IMAGE53$
Устремим N к бесконечности, получим
$IMAGE54$
Гипотеза оказалась верна, при условии что обе последовательности $IMAGE36$ и $IMAGE37$ заданы явными формулами
$IMAGE38$[(1+ $IMAGE39$)n/2]
$IMAGE37$ =[(3+ $IMAGE41$)n/2]
Но Акулич не первый догадался представить последовательности $IMAGE36$ и $IMAGE37$ в виде [ $IMAGE63$] и [ $IMAGE64$].
Эти же явные формулы получаются из формул Рэлея при x = 2/(1+ $IMAGE41$), поскольку при этом величина 1-x равна как раз 2/(3+ $IMAGE41$), т.е.
$IMAGE67$
Возникает вопрос об единственности разбиения множества N на две последовательности.
В статье Баабабова [2] доказывается теорема, обобщающая этот результат и утверждает, что таких разбиений натурального ряда существует бесконечно много. Приведем данную теорему и ее подробное доказательство.
Обозначим
$IMAGE67$
Теорема.
Если $IMAGE15$ и $IMAGE52$ - положительные иррациональные числа, связанные соотношением $IMAGE71$, то среди чисел вида [ $IMAGE63$] и [ $IMAGE64$] , где n $IMAGE74$, каждое натуральное число встречается ровно один раз.
Доказательство:
Поскольку $IMAGE15$> 1, в последовательности $IMAGE76$ никакое число не повторяется. Аналогично вследствие неравенства $IMAGE52$>1 строго возрастает и последовательность $IMAGE78$
Действительно, пусть [ $IMAGE15$] – k
$IMAGE80$
Следовательно, $IMAGE81$
Докажем теперь, что каждое натуральное число встречается ровно один раз.
Предположим, что некоторое натуральное число k вошло в обе последовательности т е k = $IMAGE82$, где m,n – натуральные числа. Тогда должны быть выполнены неравенства
k< $IMAGE83$< k + 1, k< $IMAGE64$<k + 1,
т.е.
$IMAGE85$ $IMAGE86$
сложим эти неравенства, не забывая про условие
$IMAGE71$
Получим
$IMAGE88$
откуда k<m+n<k+1
Но такого для натуральных чисел не может быть. Значит, число k не могло войти в обе последовательности.
Теперь предположим, что k не вошло ни в одну из последовательностей. Тогда для некоторых натуральных чисел m и n должны выполняться неравенства
$IMAGE15$m < k <k+1< $IMAGE15$(m+1)
$IMAGE52$n < k <k+1< $IMAGE52$(n+1)
которые можно преобразовать к виду
$IMAGE93$
складывая, получаем
$IMAGE94$
откуда m+n<k и k+1<m+n+2 $IMAGE95$m+n<k и m+n>k-1
Такого для натуральных чисел тоже не может быть. Получаем противоречие, следовательно, теорема доказана.
В следующем параграфе рассмотрены упражнения о разбиениях натурального ряда, при решении которых используются результаты данного параграфа.
§3. Упражнения
Упражнение 1
Пусть последовательность задана формулой
$IMAGE24$.Найти $IMAGE97$.
$IMAGE98$ $IMAGE99$ $IMAGE100$ $IMAGE101$ $IMAGE102$ $IMAGE103$ $IMAGE104$ $IMAGE105$
1 … 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
$IMAGE106$ $IMAGE107$ $IMAGE108$ $IMAGE109$ $IMAGE110$ $IMAGE111$ $IMAGE112$ $IMAGE113$ $IMAGE114$ $IMAGE115$ $IMAGE116$ $IMAGE117$ $IMAGE118$ $IMAGE119$ $IMAGE120$
49 50
$IMAGE97$
Используя эту формулу, можно найти любое a $IMAGE122$.
Упражнение 2.
Вычислить
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |