Техническое задание
Исходные данные:
Т = 18 Н*м
w = 56 рад/с
d = 0.55 м
схема 1
1. Электродвигатель
2. Упругая муфта
3. Редуктор с прямозубой конической передачей
4. Открытая коническая передача
5. Картофеле-очистительная машина
Задание: Рассчитать одноступенчатый редуктор с прямозубой конической передачей. Начертить сборочный чертёж редуктора, рабочие чертежи зубчатого колеса и ведомого вала.
Назначение и сравнительная характеристика привода
Данный привод используется в картофелеочистительной машине. Привод включает в себя электрический двигатель, открытую цилиндрическую косозубую передачу, одноступенчатый конический редуктор, который требуется рассчитать и спроектировать в данном курсовом проекте.
Редуктором называется механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи мощности от двигателя к рабочей машине. Кинематическая схема привода может включать, помимо редуктора, открытые зубчатые передачи, цепную или ремённую. Назначение редуктора понижение угловой скорости и повышение вращательного момента ведомого вала по сравнению с валом ведущим. Редуктор состоит из корпуса, в котором помещают элементы передачи - зубчатые колёса, валы подшипники и т.д.
Зубчатые передачи
Наиболее часто используют цилиндрические и конические передачи с прямыми и косыми зубьями. Кроме этих передач используют винтовые, и передачи с шевронными и криволинейными зубьями.
Преимущества зубчатых передач
1. Постоянство передаточного числа (для прямозубой цилиндрической U=2¸4, косозубой цилиндрической U=4¸6, для конической U=2¸3)
2. Высокая нагрузочная способность
3. Высокий КПД (0.96¸0.99)
4. Малые габариты
5. Большая долговечность, прочность, надёжность, простота в обслуживании
6. Сравнительно малые нагрузки на валы и опоры
Недостатки зубчатых передач
1. Невозможность без ступенчатого изменения скорости.
2. Высокие требования к точности изготовления и монтажа.
3. Шум при больших скоростях.
4. Плохие амортизационные свойства, что отрицательно сказывается на компенсацию динамических нагрузок.
5. Громоздкость при больших межосевых расстояниях.
6. Потребность в специальном оборудовании и инструменте для нарезания зубьев.
7. Зубчатые передачи не предохраняют от опасных нагрузок
Конические передачи по сравнению с цилиндрическими наиболее сложны в изготовлении и монтаже т.к. для них требуется большая точность.
1. Выбор электродвигателя и кинематический расчёт.
1.1 Определяем требуемую мощность двигателя
N=N*w (Вт) Т=Твых=Т3
N=56*18=1008 Bт
1.2 Определяем КПД
h=hр*hоп*пк р-редуктора
h=0,97*0,96*0,9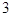 
=0,679 оп-открытой передачи
пк-подшипников качения
1.3 Определяем мощность двигателя
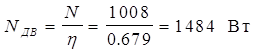
1.4 Выбираем эл. Двигатель из условия
Nн ³ Nдв Nн=1.5 кВт 4А80А2У3 Nн=1.5 кВт nс=3000
Номинальной мощности 1.5 кВт соответствует четыре вида двигателей (таблица 1)
таблица 1
| N° | Типоразмер | nc, об/мин |
| 1 | 4А80А2У3 | 3000 |
| 2 | 4А80В493 | 1500 |
| 3 | 4A90L693 | 1000 |
| 4 | 4A100L893 | 750 |
1.5 Определяем передаточное отношение двигателя
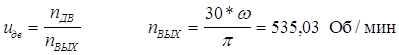, где nдв - синхронная частота вращения, Об/мин;
nвых - частота вращения выходного вала механизма (вал С, см схему 1), Об/мин
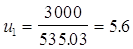
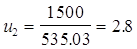
$IMAGE6$ $IMAGE7$
1.6 Задаёмся передаточным отношением открытой передачи
u = 2¸3
1.7 Определяем передаточное отношение редуктора
Передаточное отношение редуктора должно входить в промежуток для конической прямозубой передачи U=2¸3
$IMAGE8$, где U - передаточное отношение двигателя
Uоп - передаточное отношение открытой
передачи
Uр - передаточное отношение редуктора
$IMAGE9$ $IMAGE10$
Остановим свой выбор двигателе N°1, и примем следующие передаточные отношения:
uдв = 5,6 uр = 2,8 uоп = 2
Эскиз двигателя в приложении 1.
1.8 Определяем крутящие моменты действующие на валах передаточных меанизмов. $IMAGE11$
$IMAGE12$
1.9 Определяем угловую скорость на валах передаточного механизма
$IMAGE13$
Проверка: Nдв=Тдв*wдв
Nдв=4,73*313,6=1483 Вт
Двигатель 4А80А2У3
1.10 Выполняем обратный пересчёт Т3, w3 с учётом выбранного двигателя
$IMAGE14$
$IMAGE15$
$IMAGE16$
$IMAGE17$
$IMAGE18$
Проверка Nдв=Тдв*wдв
Nдв=4.19*56=1500 Вт
В дальнейшем будем вести расчёты с учётом полученных значений
1.11 Определение частоты вращения валов передаточного механизма
n1 = nc = 3000 об/мин
$IMAGE19$
Данные расчётов сведём в таблицу:
таблица 2
| | Тi, Н*м | wi, рад/с | ni, об/мин |
| Вал А | 4.78 | 314 | 3000 |
| Вал В | 9.08 | 157 | 1071 |
| Вал С | 24 | 56 | 535 |
2. Геометрический прочностной расчёт закрытой передачи.
2.1 Выбираем материал
Для шестерни и колеса выбираем сталь углеродистую качественную 45; Ст 45, для которой допускаемое напряжение при изгибе для нереверсивных нагрузок [s0]=122 МПа, допускаемое контактное напряжение [s]=550 МПа
-
рис1. Передача коническими зубчатыми колёсами
2.2 Определяем внешний делительный диаметр (см. Рис.1)
коэффициент КНb=1,2
коэффициент ширины венца по отношению к внешнему конусному
расстоянию YВRE=0,285
$IMAGE20$ [1],
где Тр - момент на выходном валу редуктора (табл. 2);
de2 - внешний делительный диаметр, мм;
[s]к - допускаемое контактное напряжение, МПа;
up - передаточное отношение редуктора;
Принимаем по ГОСТ 12289-76 ближайшее стандартное значение
de2=100мм
2.3 Принимаем число зубьев на шестерне
Z1=22
2.4 Определяем число зубьев на колесе
Z2=uр*Z1=2,8*22=62 [1]
Определяем геометрические параметры зубчатой передачи
2.5 Внешний окружной модуль
$IMAGE21$ [1]
2.6 Угол делительного конуса для (см. Рис.1):
шестерни $IMAGE22$
колеса $IMAGE23$
2.7 Определяем внешний диаметр шестерни и колеса (см. Рис.1)
$IMAGE24$
2.8 Определяем внешнее конусное расстояние (см. Рис.1)
$IMAGE25$ [1]
2.9 Определяем среднее конусное расстояние (см. Рис.1)
$IMAGE26$, где b - длина зуба
2.10 Определяем средний окружной модуль
$IMAGE27$
2.11 Определяем средний делительный диаметр шестерни и колеса (см. Рис.1)
d=m*Z [1] d1=1.3*22=28.6 мм
d2=1.3*62=80.6 мм
2.12 Определяем усилие действующее в зацеплении
окружное колеса
$IMAGE28$
шестерни
$IMAGE29$, где Т - крутящий
момент на выходном валу; d - средний делительный диаметр
радиальное $IMAGE30$ $IMAGE31$, где Р - окружное усилие, d - угол делительного конуса, a = 20°
Проверка
коэффициент ширины шестерни по среднему диаметру
$IMAGE32$ [1]
средняя окружная скорость колеса
$IMAGE33$ [1]
степень точности n=7
Для проверки контактных напряжений определяем коэффициенты нагрузок
$IMAGE34$ [1], где КНb - коэффициент учитывающий распределение нагрузки по длине зуба;
КНa - коэффициент учитывающий распределение нагрузки между прямыми зубьями;
КНV - коэффициент учитывающий динамическую нагрузку в зацеплении для прямозубых колёс
$IMAGE35$ [1]
Проверку контактных напряжений выполним по формуле:
$IMAGE36$
Проверка зубьев на выносливость по напряжениям изгиба
$IMAGE37$ [1] , где
коэффициент нагрузок
$IMAGE38$, где КFb - коэффициент концентрации нагрузки;
КFV - коэффициент динамичности
Y - коэффициент формы зубьев выбираем в зависимости от эквивалентных чисел зубьев:
для шестерни
$IMAGE39$
для колеса
$IMAGE40$
При этих значениях ZV выбираем YF1 = 3.976, YF2 = 3.6
Для шестерни отношение
$IMAGE41$
для колеса
$IMAGE42$
Дальнейший расчёт ведём для зубьев шестерни, т.к. полученное отношение для него меньше.
Проверяем зуб колеса
$IMAGE43$
3. Разработка эскизной компоновки.
3.1 Предварительный расчёт валов редуктора.
Расчёт выполняем на кручение по пониженным допускаемым напряжениям
Крутящие моменты в поперечных сечениях валов:
ведущего Тк1=Т1=9000 Нм
ведомого Тк2=Т2=24000 Нм
Диаметр выходного конца вала dв1 (см. рис. 3) определяем при допускаемом напряжении [tк]=25 МПа
$IMAGE44$ [1]
диаметр под подшипниками примем dп1=17 мм; диаметр под шестерней dк1=20 мм.
Диаметр выходного конца вала dв2 (см. рис. 4) при допускаемом напряжении [tк]=25 МПа
$IMAGE45$
диаметр под подшипниками примем dп2=20 мм; диаметр под зубчатым колесом dк2=25 мм.
3.2 Конструктивные размеры шестерни и колеса