МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
математический факультет
Кафедра алгебры и геометрии
Произведение двух групп
Курсовая работа
Исполнитель:
студентка группы H.01.01.01 М-31
Закревская С.А.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии
Монахов В. С.
Гомель 2005
Содержание
Введение
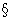1 О произведении двух групп, одна из которых содержит циклическую подгруппу индекса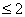 
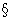2 О произведении двух групп с циклическими подгруппами индекса 2
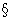3 Произведение разрешимой и циклической групп
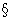3.1. Вспомогательные результаты
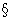3.2. Доказательства теорем 1 и 2
Заключение
Список литературы
Введение
Данную работу можно рассматривать как продолжение трудов Б. Хупперта и В. Скотта. В ней приводятся свойства конечных групп, являющихся произведением двух групп, а именно являющихся произведением двух групп, одна из которых содержит циклическую подгруппу индекса 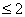, произведением двух групп с циклическими подгруппами индекса 2, произведением разрешимой и циклической групп.
Рассматриваются вопросы разрешимости, сверхразрешимости и изоморфизма конечных групп, с приведенными выше свойствами и приводится описание двух классов неразрешимых факторизуемых групп. Так же приводятся доказательства следующих теорем:
Теорема 1.1 . Если $IMAGE8$ и $IMAGE9$ - группы с циклическими подгруппами индексов 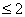, то конечная группа $IMAGE11$ разрешима.
Теорема 1.2 . Пусть $IMAGE8$ - группа Шмидта, а $IMAGE9$ - группа с циклической подгруппой индекса 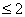. Если $IMAGE11$ и $IMAGE16$ - конечная неразрешимая группа, то $IMAGE17$ изоморфна подгруппе $IMAGE18$, содержащей $IMAGE19$, для подходящего $IMAGE20$.
Теорема 1.3 . Пусть $IMAGE8$ - 2-разложимая группа, а группа $IMAGE9$ имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если $IMAGE11$ и $IMAGE16$ - конечная неразрешимая группа, то $IMAGE17$ изоморфна подгруппе $IMAGE18$, содержащей $IMAGE19$, для подходящего $IMAGE20$.
Теорема 2.1 . Пусть конечная группа $IMAGE29$, где $IMAGE8$ и $IMAGE9$ - группы с циклическими подгруппами индексов 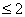. Тогда $IMAGE16$ разрешима, $IMAGE34$ и $IMAGE35$ для любого простого нечетного $IMAGE36$.
Теорема 2.2 . Если группы $IMAGE8$ и $IMAGE9$ содержат циклические подгруппы нечетных порядков и индексов 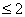, то конечная группа $IMAGE29$ сверхразрешима.
Теорема 2.3 . Пусть конечная группа $IMAGE29$, где $IMAGE8$ - циклическая подгруппа нечетного порядка, а подгруппа $IMAGE9$ содержит циклическую подгруппу индекса 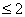. Если в $IMAGE16$ нет нормальных секций, изоморфных $IMAGE46$, то $IMAGE16$ сверхразрешима.
Теорема 3.1 . Пусть конечная группа $IMAGE16$ является произведением разрешимой подгруппы $IMAGE8$ и циклической подгруппы $IMAGE9$ и пусть $IMAGE51$. Тогда $IMAGE52$, где $IMAGE53$ - нормальная в $IMAGE16$ подгруппа, $IMAGE55$ и $IMAGE56$ или $IMAGE57$ для подходящего $IMAGE20$.
Теорема 3.2 . Конечная группа, являющаяся произведением 2-нильпотентной подгруппы и циклической подгруппы, непроста. Если циклический фактор имеет нечетный порядок, то группа разрешима.
Теорема 3.3 . Если $IMAGE29$ - простая группа, где $IMAGE8$ - холловская собственная в $IMAGE16$ подгруппа, а $IMAGE9$ - абелева $IMAGE36$-группа, то $IMAGE64$ есть расширение группы, изоморфной секции из $IMAGE65$, с помощью элементарной абелевой 2-группы. В частности, если $IMAGE9$ циклическая, то $IMAGE64$ есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
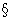1. О произведении двух групп, одна из которых содержит циклическую подгруппу индекса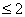
Доказывается, что конечная группа $IMAGE11$ разрешима, если группы $IMAGE8$ и $IMAGE9$ содержат циклические подгруппы индексов $IMAGE73$. Приводится описание двух классов неразрешимых факторизуемых групп. Библ. 18 назв.
В работе Б. Хупперт установил разрешимость конечной группы, которая является произведением двух диэдральных подгрупп. В. Скотт получил разрешимость группы $IMAGE11$, допустив в качестве множителей $IMAGE8$ и $IMAGE9$ еще так называемые дициклические группы. Диэдральные и дициклические группы содержат циклические подгруппы индекса 2, но не исчерпывают весь класс групп с циклическими подгруппами индекса 2. В настоящей заметке доказана
Теорема 1 . Если $IMAGE8$ и $IMAGE9$ - группы с циклическими подгруппами индексов 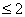, то конечная группа $IMAGE11$ разрешима.
Если подгруппа $IMAGE8$ нильпотентна, а в $IMAGE9$ есть циклическая подгруппа индекса 2, то, как показали H. Ито и Б. Хупперт, конечная группа $IMAGE11$ разрешима. Дополнением этого результата являются теоремы 2 и 3.
Теорема 2 . Пусть $IMAGE8$ - группа Шмидта, а $IMAGE9$ - группа с циклической подгруппой индекса 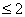. Если $IMAGE11$ и $IMAGE16$ - конечная неразрешимая группа, то $IMAGE17$ изоморфна подгруппе $IMAGE18$, содержащей $IMAGE19$, для подходящего $IMAGE20$.
$IMAGE93$ обозначает наибольшую разрешимую инвариантную в $IMAGE16$ подгруппу. Группой Шмидта называется ненильпотентная группа, все собственные подгруппы которой нильпотентны.
Теорема 3 . Пусть $IMAGE8$ - 2-разложимая группа, а группа $IMAGE9$ имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если $IMAGE11$ и $IMAGE16$ - конечная неразрешимая группа, то $IMAGE17$ изоморфна подгруппе $IMAGE18$, содержащей $IMAGE19$, для подходящего $IMAGE20$.
Частным случаем теоремы 3, когда $IMAGE8$ - абелева, а $IMAGE9$ имеет порядок $IMAGE105$, $IMAGE36$ - простое число, является теорема 8 Б. Хупперта.
Доказательства теорем 1--3 и составляют содержание настоящей заметки.
Рассматриваются только конечные группы. Все используемые определения и обозначения стандартны, их можно найти в обзоре С. А. Чунихина и Л. А. Шеметкова.
Вначале докажем несколько лемм.
Лемма 1 . Пусть в группе существует циклическая подгруппа индекса 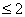. Тогда каждая подгруппа и фактор-группа обладает, циклической подгруппой индекса 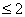. Доказательство осуществляется непосредственной проверкой.
Лемма 2 . Пусть $IMAGE11$, $IMAGE8$ - собственная подгруппа группы $IMAGE16$, $IMAGE9$ - подгруппа четного порядка с циклической силовской 2-подгруппой. Если $IMAGE113$, то $IMAGE16$ содержит подгруппу индекса 2.
Доказательство. Если $IMAGE8$ содержит инвариантную в $IMAGE16$ подгруппу $IMAGE117$, то фактор-группа $IMAGE118$ удовлетворяет условиям леммы. По индукции $IMAGE118$ обладает подгруппой индекса 2, поэтому и в $IMAGE16$ есть подгруппа индекса 2.
Пусть $IMAGE8$ не содержит инвариантных в $IMAGE16$ подгрупп $IMAGE123$. Тогда представление группы $IMAGE16$ подстановками правых смежных классов по $IMAGE8$ есть точное степени $IMAGE126$, где $IMAGE127$. Группу $IMAGE16$ можно отождествить с ее образом в симметрической группе $IMAGE129$ степени $IMAGE126$. Так как в $IMAGE9$ силовская 2-подгруппа $IMAGE132$ циклическая, то $IMAGE133$, где $IMAGE134$ - инвариантное 2-дополнение. Пусть $IMAGE135$, $IMAGE136$. $IMAGE137$, $IMAGE138$ и $IMAGE139$. Подстановка $IMAGE140$ разлагается в произведение циклов
$IMAGE141$
т. е. подстановка $IMAGE140$ имеет $IMAGE143$ циклов, каждый длины $IMAGE144$. Декремент подстановки равен $IMAGE145$ и есть нечетное число, поэтому $IMAGE140$ - нечетная подстановка. Теперь $IMAGE147$, а так как индекс $IMAGE148$ в $IMAGE129$ равен 2, то $IMAGE150$ - подгруппа индекса 2 в группе $IMAGE16$.
Лемма 2 обобщает лемму А. В. Романовского.
Замечание. Простая группа $IMAGE152$ является произведением двух подгрупп $IMAGE8$ и $IMAGE9$, причем $IMAGE155$, а $IMAGE9$ - группа порядка $IMAGE157$ с циклической силовской 2-подгруппой. Этот пример показывает, что требование $IMAGE113$ отбросить нельзя.
Лемма 3 . Пусть $IMAGE16$ - дважды транзитивная группа подстановок на множестве $IMAGE160$ и пусть $IMAGE161$ - стабилизатор некоторой точки $IMAGE162$. Тогда все инволюции из центра $IMAGE161$ содержатся в $IMAGE164$.
Доказательство. Пусть $IMAGE165$. Допустим, что существует $IMAGE166$, причем $IMAGE167$. Так как $IMAGE161$ транзитивна на $IMAGE169$, то $IMAGE170$. Ho $IMAGE171$, поэтому $IMAGE172$ и $IMAGE173$ - тождественная подстановка. Противоречие. Следовательно, $IMAGE173$ фиксирует только $IMAGE175$. Теперь подстановка $IMAGE173$ содержит только один цикл длины 1, а так как $IMAGE173$ - инволюция, то $IMAGE178$ нечетен. Но $IMAGE179$, поэтому существует силовская 2-подгруппа $IMAGE180$ из $IMAGE16$ с $IMAGE182$ и $IMAGE183$. Если $IMAGE184$, то $IMAGE185$, отсюда $IMAGE186$ и $IMAGE187$, т. е. $IMAGE188$. Теперь $IMAGE189$ и из теоремы Глаубермана следует, что $IMAGE190$.
Лемма 4 . Пусть центр группы $IMAGE8$ имеет четный порядок и силовская 2-подгруппа из $IMAGE8$ либо циклическая, либо инвариантна в $IMAGE8$. Если $IMAGE9$ - группа с циклической подгруппой индекса 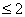, то группа $IMAGE11$ непроста.
Доказательство. Пусть $IMAGE197$ - циклическая подгруппа в $IMAGE9$, для которой $IMAGE199$, а $IMAGE200$ - максимальная в $IMAGE16$ подгруппа, содержащая $IMAGE8$. Тогда $IMAGE203$. Если $IMAGE204$, то $IMAGE205$ и по лемме С. А. Чунихина группа $IMAGE16$ непроста. Значит, $IMAGE207$.
Допустим, что порядок $IMAGE197$ нечетен. Если $IMAGE209$, то $IMAGE210$. Если $IMAGE211$, то ввиду леммы 2 $IMAGE212$ и поэтому опять $IMAGE210$. Рассмотрим представление $IMAGE16$ подстановками смежных классов по $IMAGE8$. Так как $IMAGE8$ - максимальная в $IMAGE16$ подгруппа, то $IMAGE16$ - примитивная группа подстановок степени $IMAGE219$. Если $IMAGE219$ - простое число, то $IMAGE16$ либо разрешима, либо дважды транзитивна. Если $IMAGE219$ - составное число, то, так как $IMAGE197$ - регулярная группа подстановок при этом представлении, $IMAGE16$ - опять дважды транзитивна. Из леммы 3 следует, что $IMAGE16$ непроста.
Пусть порядок $IMAGE197$ четен. Если $IMAGE227$, то $IMAGE228$ непроста по лемме 2. Значит, $IMAGE229$ и $IMAGE210$. Пусть $IMAGE180$ - силовская 2-подгруппа из $IMAGE8$. Если $IMAGE180$ инвариантна в $IMAGE8$, то $IMAGE180$ инвариантна и в $IMAGE16$. Следовательно, $IMAGE180$ - циклическая группа. Но $IMAGE180$ не является силовской в $IMAGE16$, поэтому $IMAGE180$ содержится как подгруппа индекса 2 в некоторой группе $IMAGE241$. Теперь для инволюции $IMAGE173$ из центра $IMAGE8$ имеем $IMAGE244$, т. е. $IMAGE8$ не максимальная в $IMAGE16$. Противоречие.
Следствие. Пусть группа $IMAGE11$, где группа $IMAGE9$ содержит циклическую подгруппу индекса 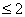. Если $IMAGE8$ - 2-разложимая группа четного порядка, то группа $IMAGE16$ непроста.
Лемма 5 . Пусть группа $IMAGE8$ содержит циклическую инвариантную подгруппу нечетного порядка и индекса 2. Если $IMAGE9$ - 2-разложимая группа, то группа $IMAGE11$ разрешима.
Доказательство. Применим индукцию к порядку $IMAGE16$. Если $IMAGE256$, то ввиду леммы 1 фактор-группа $IMAGE17$ удовлетворяет условиям леммы. По индукции, $IMAGE17$ разрешима, отсюда разрешима и $IMAGE16$.
Пусть $IMAGE260$. Если $IMAGE8$ - циклическая, то $IMAGE16$ разрешима по теореме В. А. Ведерникова. Поэтому $IMAGE263$, $IMAGE197$ - циклическая подгруппа индекса 2, $IMAGE265$. Пусть $IMAGE266$, где $IMAGE267$ - силовская 2-подгруппа из $IMAGE9$, $IMAGE134$ - ее дополнение. Если $IMAGE270$, то $IMAGE271$ разрешима. Теперь $IMAGE272$ и $IMAGE273$ можно считать силовской 2-подгруппой в $IMAGE16$. Так как $IMAGE275$ и $IMAGE276$, то $IMAGE277$. Пусть $IMAGE278$ и $IMAGE279$. Тогда $IMAGE280$ и $IMAGE281$. По лемме С. А. Чунихина подгруппа $IMAGE282$ максимальна в $IMAGE16$ и $IMAGE284$. Представление группы $IMAGE16$ подстановками смежных классов по подгруппе $IMAGE16$ дважды транзитивное: если $IMAGE219$ - простое число, если $IMAGE219$ - составное. Из леммы 3 вытекает теперь, что $IMAGE256$.Противоречие.
Доказательство теоремы 1 . Применим индукцию к порядку группы G. Пусть $IMAGE290$ и $IMAGE291$ - циклические инвариантные подгруппы в $IMAGE8$ и в $IMAGE9$ соответственно, чьи индексы равны 1 или 2, а $IMAGE180$ и $IMAGE132$ - те силовские 2-подгруппы из $IMAGE8$ и $IMAGE9$, для которых $IMAGE298$ и $IMAGE299$ есть силовская 2-подгруппа $IMAGE16$. Будем считать, что $IMAGE301$. Если $IMAGE302$, то $IMAGE303$ и $IMAGE304$ разрешима по теореме Ито-Хупперта. Поэтому в дальнейшем полагаем, что $IMAGE305$. Ввиду леммы 1 каждая фактор-группа удовлетворяет условиям теоремы, поэтому $IMAGE260$
Допустим, что $IMAGE212$. Если $IMAGE308$, то $IMAGE309$ и $IMAGE310$. Так как $IMAGE8$ разрешима, то $IMAGE312$. Если $IMAGE313$, то $IMAGE314$ и $IMAGE304$ разрешима.
Пусть теперь $IMAGE113$. Тогда и $IMAGE317$. Так как $IMAGE180$ не является силовской подгруппой в $IMAGE16$, то $IMAGE180$ содержится как подгруппа индекса 2 в некоторой 2-группе $IMAGE321$. Обозначим через $IMAGE322$ силовскую 2-подгруппу из $IMAGE290$. Очевидно, что $IMAGE322$ инвариантна в $IMAGE8$.
Предположим, что $IMAGE326$ и пусть $IMAGE173$ - инволюция из $IMAGE328$. В $IMAGE290$ все подгруппы характеристические и $IMAGE290$ инвариантна в $IMAGE8$, поэтому $IMAGE332$ и $IMAGE333$. Пусть $IMAGE200$ - максимальная в