Курсова робота
Тема:
Програма, яка знаходить квадратні корені комплексних чисел
Зміст
Вступ. 3
Теорія. 4
Програма. 8
Контрольні приклади. 10
Висновок. 11
Література. 12
Протягом курсу елементарної алгебри кілька разів відбувається збагачення запасу чисел. Школяр, що приступає до вивчення алгебри, приносить з арифметики знайомство з позитивними і дробовими числами. Алгебра починається власне кажучи з уведення негативних чисел, тобто з оформлення першої серед важливішої числових систем – системи цілих чисел, що складаються з усіх позитивних і всіх негативних цілих чисел і нуля, і більш широкої системи раціональних чисел, що складається з усіх цілих чисел і всіх дробових чисел, як позитивних, так і негативних.
Подальше розширення запасу чисел відбувається тоді, коли в розглядання вводяться ірраціональні числа. Система, що складається з раціональних і всіх ірраціональних чисел, називається системою дійсних (чи речовинних) чисел. Строга побудова системи дійсних чисел міститься звичайно в університетському курсі математичного аналізу; для нас, однак, було досить у попередніх главах і буде досить надалі того знайомства з дійсними числами, якої володіє читач, який приступає до вивчення вищої алгебри.
Нарешті, у самому кінці курсу елементарної алгебри система дійсних чисел залишається для читача менш звичної, звичайно, чим система дійсних чисел, хоча насправді вона має багатьма дуже гарними властивостями.
Переходимо до питання про зведення комплексних чисел у степінь і знаходження з них кореня. Для зведення числа a=a+bi у цілу позитивний степінь n досить застосувати до вираження (a+bi) n. Формулу бінома Ньютона (ця формула справедлива і для комплексних чисел, так, як її доказ заснований лише на законі дистрибутивності), а потім скориставшись рівностями i2= - 1, i3= - i, i4=1, відкіля взагалі
i4k= 1, i4k+1= i, i4k+2= - 1, i4k+3= - i.
Якщо число б задано в тригонометричній формі, то при цілому позитивному n випливає наступна формула, називана формулою Муавра:
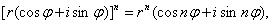(1)
тобто при зведенні комплексного числа в ступінь модуль зводиться в цей ступінь, а аргумент збільшується на показник ступеня. Формула (1) вірна і для цілих негативних показників. Дійсно, через б-n=(б-1) n, досить застосувати формулу Муавра до числа б-1.
Окремий випадок формули Муавра, а саме рівність
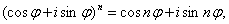
дозволяє легко одержати формули для синуса і косинуса кратного кута. Дійсно, розкриваючи ліву частину цього рівності по формулі бінома і дорівнюючи окремо дійсні і мнимі частини обох частин рівності, ми одержимо:
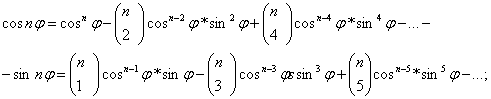
Тут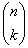 
є обічне позначення біноміального коефіцієнта:
$IMAGE6$
При n=2 ми приходимо до відомих формул
$IMAGE7$
а при n=3 до формул
$IMAGE8$
Витяг кореня з комплексних чисел представляє вже багато більше труднощів. Почнемо з витягу квадратного кореня з числа б=a+bi. Ми не знаємо поки, чи існує таке комплексне число, квадрат якого дорівнює б. Припустимо, що таке число u+vi існує тобто, уживаючи звичайну символіку, можна написати:
$IMAGE9$
З рівності
(u+vi) 2=a+bi
випливає
$IMAGE10$ (2)
Зводячи в квадрат обидві частини кожного з рівностей (2), а потім складаючи їх одержуємо:
$IMAGE11$
відкіля
$IMAGE12$
позитивний знак узятий тому, що числа u i v дійсні, і тому ліва частина рівності позитивна. З цієї рівності і з першого з рівностей (2) одержуємо:
$IMAGE13$
Ми приходимо, витягаючи корені, до двох значень для u, що відрізняється друг від друга знаком, а також до двох значень для v. Усі ці значення будуть дійсними, тому що квадратні корені будуть шукаються при будь-яких a і b з позитивних чисел. Отримані значення для u і v не можна комбінувати між собою довільним образом, тому що, через другий з рівностей (2), знак добутку uv повинний збігатися зі знаком b. Це дає дві можливі комбінації значень u і v, тобто два числа виду u+vi, що можуть служити значеннями квадратного кореня з числа б. Ці числа відрізняються друг від друга знаком. Елементарна, хоча і громіздка, перевірка (зведенням отриманих чисел у квадрат, окремо для випадку b>0 і для випадку b<0) показує, що знайдені нами числа дійсно є значеннями квадратного кореня з числа б. Таким чином, витяг квадратного кореня з комплексного числа завжди можливо і дає два значення, що відрізняються друг від друга знаком.
Зокрема, тепер робиться можливим витяг квадратного кореня і з негативного дійсного числа, причому значення цього кореня будуть чисто мнимими. Справді, якщо a<0 і b=0, то $IMAGE14$, тому що цей корінь повинний бути позитивним, а тоді $IMAGE15$ тобто u=0, відкіля $IMAGE16$.
Спроби витягу з комплексних чисел, заданих у виді a+bi, коренів більш високого ступеня, чим друга, зустрічаються з невизначеними ускладненнями. Так, якби ми захотіли в такий же спосіб витягти з числа a+bi кубічний корінь, те повинні були б вирішити деяке допоміжне кубічне рівняння. З іншого боку, тригонометрична форма дуже добре пристосована для витягу коренів будь-якого ступеня і, користаючись нею, ми зараз цілком вичерпаємо це питання.
Нехай потрібно витягти корінь n-й ступеня з числа $IMAGE17$ Припустимо, що це зробити можна і що в результаті вийде число $IMAGE18$ тобто
$IMAGE19$ (3)
Тоді, по формулі Муавра, $IMAGE20$, тобто $IMAGE21$ де в правій частині коштує однозначно визначене позитивне значення кореня n-й ступеня з позитивного дійсного числа r. З іншого боку, аргумент лівої частини рівності (3) є n0. Не можна затверджувати, однак, що n0 дорівнює $IMAGE22$, тому що ці кути можуть у дійсності відрізнятися на доданок, що є деяким цілим кратним числа $IMAGE23$. Тому $IMAGE24$, де до – ціле число, відкіля
$IMAGE25$
Назад, якщо ми беремо число $IMAGE26$ те при будь-якім цілому до, позитивним чи негативної, n-я ступінь цього числа дорівнює б. Таким чином,
$IMAGE27$ (4)
Даючи до різні значення, ми не завжди будемо одержувати різні значення шуканого кореня. Дійсно, при
$IMAGE28$ (5)
ми одержимо n значень кореня, що усі будуть різними, тому що збільшене то на одиницю спричиняє збільшення аргументу на $IMAGE29$. Нехай тепер до довільно. Якщо k=nq+r, $IMAGE30$ то
$IMAGE31$
тобто значення аргументу при нашому до відрізняється від значення аргумента при k=r на число, кратне $IMAGE23$, ми одержуємо, отже таке ж значення кореня, як при значенні до, рівному r, тобто вхідним у систему (5).
Опис програми
n-показник степеня кореня;
a,b,f – дійсна, уявна частини та аргумент z;
$IMAGE33$;
i – номер кореня;
x,y – масиви дійсних та уявних частин коренів.
Нижче наведений приклад програми у роботі:
$IMAGE34$
uses crt; const dim=20; type ar=array [1. . dim] of real; var a1,b1: real; n1, i1: integer;
x,y: ar;
function sgn(xx: real): integer;
begin
if xx>0 then sgn: =1
else if xx<0 then sgn: =-1
else sgn: =0;
end;
procedure rootcom(a,b: real; n: integer; var x,y: ar);
var c,r,f: real;
i: integer;
begin
r: =a*a+b*b;
if r<>0 then r: =exp(ln(r) /2/n);
if a=0 then f: =sgn(b) *pi/2 else
if a>0 then f: =arctan(b/a) else
if b<0 then f: =arctan(b/a) - pi else f: =arctan(b/a) +pi;
f: =f/n;
c: =2*pi/n;
for i: =1 to n do
begin x [i]: =r*cos(f); y [i]: =r*sin(f); f: =f+c; end;
end;
begin clrscr;
textcolor(10);
write('ўўҐ¤iвм ¤i©бг з бвЁгà');
textcolor(white);
read(a1);
textcolor(10);
write('ўўҐ¤iвм гпўг з бвЁгà');
textcolor(white);
read(b1);
textcolor(10);
write('ўўҐ¤iвм Ї®Є §ЁЄ б⥯Ґпà');
textcolor(white);
read(n1);
rootcom(a1,b1,n1,x,y);
writeln('Љ Ћ ђ … H џ');
for i1: =1 to n1 do
writeln(i1,') ',x [i1]: 1: 2,'+i*(',y [i1]: 1: 2,') ');
readkey;
end.
Приклад 1
$IMAGE35$
Приклад 2
$IMAGE36$
Приклад 3
$IMAGE37$
Таким чином, витяг коренів n-й ступеня з комплексного числа б завжди можна і дає n різних значень. Усі значення коренів n-й ступені розташовані на окружності радіуса $IMAGE38$ з центром у нулі і поділяють цю окружність на n рівних частин.
Зокрема, корінь n - й ступеня з дійсного числа б так само має n різних значень, дійсних серед цих значень буде два, одне чи ні одного в залежності від знака б і парності n.
1. А.Г. Курош "Курс высшей алгебры", "Наука", Москва 1975
2. С.Т. Завало, В.М. Костарчук, Б.И. Хацет "Алгебра и теория чисел", Том 1,"Высшая школа", Киев 1974
3. С.Т. Завало, В.М. Костарчук, Б.И. Хацет "Алгебра и теория чисел", Том 2,"Высшая школа", Киев 1976