База рефератов

Министерство образования и науки Украины

Донецкий государственный институт искусственного интеллекта

Донецкий лицей «Интеллект»

Кафедра математики и информатики

Научная работа

на тему: «Применение неравенств при решении олимпиадных задач».

( электронный учебник )

Выполнила:

ученица 11-Г класса

Борисенкова О.Д.

Научный руководитель:

Степанов Т.Л.

Донецк 2006

СОДЕРЖАНИЕ

Введение

1 Постановка задачи

2 Актуальность

3 Реализация задачи

3.1 Теоретические сведения

3.2 Решение задач с применением данных неравенств

3.3 Сборник задач

3.4 Тесты

4 Инструкция по пользованию

Выводы

Список использованной литературы

ВВЕДЕНИЕ

При решении задач, предлагаемых на вступительных письменных экзаменах и олимпиадах по математике, могут быть использованы любые известные абитуриентам математические методы. При этом разрешается пользоваться и такими, которые не изучаются в общеобразовательной школе.

Все это свидетельствует о необходимости самостоятельного изучения абитуриентами математических методов, в основе которых лежат понятия и положения, не входящие в программу по математике общеобразовательной школы. К таким понятиям, например, относятся неравенства Коши, Коши-Буняковского, Бернулли и Йенсена.

1. ПОСТАНОВКА ЗАДАЧИ

Таким образом, целью данной работы является разработка электронного обучающего пособия, в котором будет предложен материал по выбранной теме. Т.е. в учебнике будут предоставлены теоретические сведения по всем неравенствам, примеры применения этих неравенств в решении олимпиадных задач, сборник задач для самостоятельного решения, решения к ним, а также тестовые вопросы, которые позволят оценить себя и проверить уровень полученных знаний.

Для реализации поставленной задачи был выбран язык электронной разметки текста HTML.

2. АКТУАЛЬНОСТЬ

Данная разработка рассчитана на учащихся, которые имеют довольно-таки высокий уровень знаний в области математики, причем как в пределах, так и вне школьной программы, но все равно хотят его повысить. Т.е. этот учебник будет очень полезным для самостоятельного изучения темы и подготовки к олимпиадам ІІ-ІІІ этапов.

Также очень удобен и прост в применении, для работы с ним не требуется никаких специальных программ или дополнительных приложений, кроме стандартного Internet-браузера.

Важным пунктом является то, что в учебнике собрана информация по теме неравенств, которую в принципе довольно-таки сложно найти, причем так, чтобы она была в одном и том же печатном издании. Большая часть сведений по некоторым неравенствам была найдена только в периодических изданиях, журналах. Здесь же все собрано воедино, информация представлена кратко, но исчерпывающе для того, чтобы разобраться и понять.

3. РЕАЛИЗАЦИЯ ЗАДАЧИ

3.1 Теоретические сведения

Неравенство Йенсена

Теорема (неравенство Йенсена):

Пусть  – функция, выпуклая на некотором интервале, x₁, x ₂, …, x _n – произвольные числа из этого интервала, а α₁, α₂, …, α_n – произвольные положительные числа, сумма которых равна единице. Тогда:

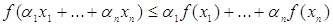. (1)

Доказательство:

Рассмотрим на графике функции  точки А₁, А₂, …, А_n с абсциссами х₁, x₂, …, x_n. Расположим в этих точках грузы с массами, m₂, …, m_n. Центр масс этих точек имеет координаты

.

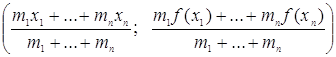Так как точки А₁, А₂, …, А_n принадлежат надграфику выпуклой функции, то и их центр масс также принадлежит надграфику (ибо надграфик – выпуклая фигура). А это означает, что ордината центра масс М не меньше ординаты точки на графике с той же абсциссой (рис. 1), т.е.

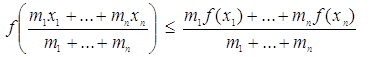. (2)

	$IMAGE6$

рис. 1

Для завершения доказательства остаётся положить m₁= α₁, …, m_n= α_n.

Однако есть два важных замечания. Во-первых, в процессе доказательства неравенства Йенсена (1) мы доказали неравенство (2). На самом деле эти неравенства равносильны. Положив в неравенстве (1) $IMAGE7$ (i=1, 2, ..., n), мы получаем неравенство (2). Поэтому естественно эти два неравенства называются неравенствами Йенсена. Неравенство (1) выглядит более компактно, однако для приложений удобней пользоваться неравенством (2). Во-вторых, если функция $IMAGE8$ вогнутая, то для неё неравенства Йенсена (1) и (2) меняются на противоположные. Чтобы доказать это, достаточно рассмотреть выпуклую функцию $IMAGE9$.

Неравенство Коши-Буняковского

На первый взгляд, неравенство Йенсена не производит особого впечатления: слишком общо выглядит формулировка. Однако дальше можно убедиться, что это впечатление обманчиво.

Продемонстрировать силу неравенства Йенсена можно на конкретном примере. А именно, доказать знаменитое неравенство Коши-Буняковского $IMAGE10$, где a₁, a₂, …, a_n, b₁, b₂, …, b_n – произвольные положительные числа.

Доказательство:

Как мы знаем, функция $IMAGE11$ - выпуклая. Напишем для этой функции неравенство Йенсена (2):

$IMAGE12$, (m_i > 0).

Следовательно, $IMAGE13$. Положив $IMAGE14$, получим требуемое неравенство.

Неравенство Коши

При решении многих задач часто используется классическое неравенство Коши о среднем арифметическом и среднем геометрическим неотрицательных чисел.

Пусть x₁, x ₂, …, x _n – неотрицательные числа. Средним арифметическим этих чисел называется число –

$IMAGE15$.

Средним геометрическим чисел x₁, x ₂, …, x _n называется число –

_$IMAGE16$.

Теорема 1. Если x₁, x ₂, …, x _n – неотрицательные числа, то имеет место неравенство

$IMAGE17$. (1)

Причём знак равенства в нем достигается тогда и только тогда, когда все числа равны.

Соотношение (1) называется неравенством Коши. При n=2 неравенство Коши следует из очевидного неравенства

$IMAGE18$. Действительно, $IMAGE19$, откуда

$IMAGE20$. (2)

Отметим, что знак равенства в (2) имеет место тогда и только тогда, когда x₁=x₂.

Пусть x₁, x ₂, …, x _n – положительные числа. Средним гармоническим (средним пропорциональным) этих чисел называется число –

$IMAGE21$.

Теорема 2. Если x₁, x ₂, …, x _n – положительные числа, то имеют место неравенства

A_n ≥ G_n ≥ H_n.

Действительно, применяя к числам $IMAGE22$ неравенство Коши, получаем

$IMAGE23$ , (3)

откуда G_n ≥ H_n.

Пусть x₁, x ₂, …, x _n – произвольные числа. Средним квадратическим этих чисел называется число –

$IMAGE24$.

Теорема 3. Если x₁, x ₂, …, x _n – положительные числа, то имеют место неравенства

K_n ≥ A_n ≥ G_n ≥ H_n , или

$IMAGE25$. (4)

Причём знак равенства в (4) достигается тогда и только тогда, когда все числа равны.

Для двух чисел неравенство (4) можно записать как

$IMAGE26$,

которое очень легко доказать с помощью простых преобразований. А именно,

$IMAGE27$

аналогично доказывается и для n чисел, откуда K_n ≥ A_n.

Неравенство Бернулли

Ещё один способ решения некоторых олимпиадных задач – это использование неравенства Бернулли, которое иногда может значительно облегчить задачу. «Классическое» неравенство Бернулли формируется следующим образом:

Теорема. Для x > -1 и произвольного натурального n имеет место

$IMAGE28$ (1)

причем равенство в (1) достигается при x=0, n=0 или n=1.

Однако кроме (1) существует и более общее неравенство Бернулли, которое содержит в себе два неравенства:

если n<0 или n>1, то

$IMAGE29$, (2)

если 0<n<1, то

$IMAGE30$, (3)

где x > -1.

Следует отметить, что равенства (2) и (3) имеют место лишь при x=0.

Доказательство(I способ):

$IMAGE31$, где x_i – числа одного и того же знака и $IMAGE32$.

Применяем метод математической индукции.

Проверяем неравенство для n=1: $IMAGE33$. Неравенство верно.

Пусть неравенство верно для n членов, т.е. верно неравенство

$IMAGE31$.

Умножим его на неотрицательное число 1+x_n+1 (оно неотрицательно, т.к. $IMAGE35$). Получим:

$IMAGE36$.

Т.к. x_i одного знака, произведения в правой части положительны, и если их отбросить, неравенство только усилится. Получаем:

$IMAGE37$.

Как мы видим, неравенство верно и для n+1 членов, а значит верно для любых n.

Доказательство(II способ):

Также применяем метод математической индукции.

При n=1 имеем $IMAGE38$, $IMAGE39$. Утверждаем, что при n=k неравенство верно: $IMAGE40$. Тогда при n=k+1 имеем

$IMAGE41$.

Неравенство доказано.

Весовое (общее) неравенство Коши

Ранее мы рассмотрели так называемое классическое неравенство Коши. Однако очень большое значение имеет также одно важное обобщение неравенства Коши – это общее, или весовое, неравенство Коши.

Теорема. Для любых действительных положительных чисел m₁, m₂, …, m_n и для любых неотрицательных x₁, x₂, …, x_n имеет место неравенство

$IMAGE42$. (1)

Числа m₁, m₂, …, m_n называются весовыми коэффициентами.

Неравенство (1) выполняется и для неотрицательных весовых коэффициентов m₁, m₂, …, m_n, но в этом случае необходимо требовать, чтобы знаменатель левой части (1) не превращался в ноль и выражения $IMAGE43$имели смысл (т.е. не все m₁, m₂, …, m_n равны нулю и числа x_i и m_i одновременно не равнялись нулю).

Понятно, что при m₁= m₂= …= m_n, весовое неравенство Коши превращается в обыкновенное неравенство Коши.

Выражение, которое стоит в левой части (1), называется весовым средним арифметическим, а то, которое в правой – весовым средним геометрическим.

Неравенство (1), для натуральных m₁, m₂, …, m_n, непосредственно следует из обыкновенного неравенства Коши:

$IMAGE44$. (2)

Неравенство (1) с неотрицательными рациональными весовыми коэффициентами легко привести к случаю, когда $IMAGE45$.

3.2 Решение задач с применением данных неравенств

Неравенство Йенсена

Задача:

Пусть a₁,…, a_n > 0, $IMAGE46$. Доказать $IMAGE47$.

Решение:

Записываем неравенство Йенсена для f(x)=x², m_i=n. Получаем:

$IMAGE48$, $IMAGE49$, $IMAGE50$,

что и требовалось доказать.

Неравенство Коши-Буняковского

Задача:

Пусть a+b+c=1. Доказать, что $IMAGE51$.

Решение:

Из неравенства Коши-Буняковского имеем

$IMAGE52$.

А отсюда имеем, что $IMAGE51$.

Неравенство Коши

Задача:

Пусть a, b, c – положительные числа, сумма которых равна единице. Доказать, что

(1+a)(1+b)(1+c) ≥ 8(1-a)(1-b)(1-c).

Решение:

Поскольку a+b+c=1, то 1+a= (1-b)+(1- c). Используя неравенство Коши между средним арифметическим и средним геометрическим $IMAGE54$, получаем

$IMAGE55$.

Аналогично

$IMAGE56$,

$IMAGE57$.

Перемножая все три неравенства, получаем искомое неравенство.

Неравенство Бернулли

Задача:

Решить уравнение

$IMAGE58$.

Решение:

К каждому слагаемому левой части уравнения применяем неравенство Бернулли, тогда

$IMAGE59$,

причем равенство возможно лишь при $IMAGE60$, т.е. x=±1. Следовательно, x=±1 – корни уравнения.

Весовое (общее) неравенство Коши

Задача 1:

Для действительных положительных чисел a, b доказать неравенство $IMAGE61$.

Решение:

По весовому неравенству Коши ( $IMAGE62$), имеем

$IMAGE63$.

 Для завершения доказательства осталось учесть очевидное неравенство $IMAGE64$. Равенство достигается при a=b.

Задача 2:

Для произвольных a,b≥0 доказать неравенство

$IMAGE65$(1).

Решение:

По весовому неравенству Коши имеем,