ПРЕДСТАВЛЕННЯ І ПЕРЕТВОРЕННЯ ТОЧОК
Представлення точок здійснюється наступним чином:
На площині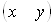 
У просторі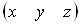 
Перетворення точок.
Розглянемо результати матричного множення 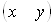, що визначає точку Р, і матриці перетворення 2х2 загального виду:
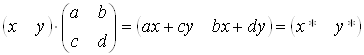(3.1)
Дослідимо декілька часткових випадків.
1) а=d=1 і c=b=0. Змін не відбувається
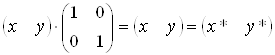. (3.2)
2) d=1, b=c=0. Зміна масштабу по осі x
$IMAGE6$. (3.3)
3) b=c=0. Зміна масштабу по осях x і y
$IMAGE7$. (3.4)
4) b=c=0, d=1, a=-1. Відображення координат відносно осі y
$IMAGE8$. (3.5)
5) b=c=0, a=d<0. Відображення відносно початку координат
$IMAGE9$. (3.6)
6) а=d=1,c=0. Зсув
$IMAGE10$. (3.7)
Для початку координат маємо інваріантно
$IMAGE11$.
$IMAGE12$
Рис.3.1. Перетворення точок.
ПЕРЕТВОРЕННЯ ПРЯМИХ ЛІНІЙ
Пряма задана 2 векторами.
Вектори положення точок А і В рівні $IMAGE13$ і $IMAGE14$.
$IMAGE15$
Рис.3.2. Перетворення прямих ліній.
Матриця перетворення
$IMAGE16$.
Одержимо:
$IMAGE17$, (3.8)
$IMAGE18$. (3.9)
Альтернативне представлення лінії AB
$IMAGE19$.
Після цього множення матриці L на Т дасть
$IMAGE20$. (3.10)
Операція зсуву збільшила довжину лінії і змінила її положення.
ОБЕРТАННЯ
Розглянемо плоский трикутник ABC.
Здійснимо поворот на 90° проти годинникової стрілки.
$IMAGE21$
Рис.3.3. Обертання і відображення.
Одержимо
$IMAGE22$. (3.11)
В результаті отримаємо трикутник A*B*C*. Поворот на 180° задається матрицею
$IMAGE23$,
поворот на 270° навколо початку координат - за допомогою матриці:
$IMAGE24$.
ВІДОБРАЖЕННЯ
Відображення визначається поворотом на 180° навколо осі, що лежить у площині ху.
1) Обертання навколо прямої y=x задається матрицею:
$IMAGE25$.
Нові вирази визначаються співвідношенням:
$IMAGE26$. (3.12)
2) Обертання навколо осі y=0 задається матрицею:
$IMAGE27$.
Нові вершини визначаються співвідношенням:
$IMAGE28$. (3.13)
ЗМІНА МАСШТАБУ
Зміна масштабу визначається значенням 2-х елементів головної діагоналі матриці.
Якщо використовуємо матрицю $IMAGE29$ маємо збільшення в 2 рази.
Якщо значення елементів не рівні, то має місце спотворення.
Трикутник ABC перетворений за допомогою матриці $IMAGE29$. Трикутник DEF перетворений за допомогою матриці $IMAGE31$. Маємо спотворення.
$IMAGE32$
Рис.3.4. Рівномірна і нерівномірна зміна масштабів.
ДВОВИМІРНИЙ ЗСУВ І ОДНОРІДНІ КООРДИНАТИ
Введемо третій компонент у вектори точок 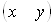і $IMAGE34$- $IMAGE35$ і $IMAGE36$.
Матриця перетворення матиме вигляд:
перетворення фігура площина точка
$IMAGE37$.
Таким чином,
$IMAGE38$. (3.14)
Константи m, n викликають зсув x* і y* відносно x і y.
Матриця 3х2 не квадратна - вона не має оберненої матриці.
Доповнимо матрицю перетворення до квадратної
$IMAGE39$. (3.15)
Третій компонент не змінюється.