Контрольная работа
Дисциплина: Высшая математика
Тема: Пределы. Сравнение бесконечно малых величин
Содержание
1. Предел числовой последовательности
2. Предел функции
3. Второй замечательный предел
4. Сравнение бесконечно малых величин
Литература
1. Предел числовой последовательности
Решение многих математических и прикладных задач приводит к последовательности чисел, заданных определенным образом. Выясним некоторые их свойства.
Определение 1.1. Если каждому натуральному числу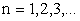 
по какому-то закону поставлено в соответствие вещественное число 
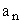, то множество чисел 
называется числовой последовательностью.
Исходя из определения 1, видно, что числовая последовательность всегда содержит бесконечное число элементов. Изучение различных числовых последовательностей показывает, что с ростом номера их члены ведут себя по-разному. Они могут неограниченно увеличиваться или уменьшаться, могут постоянно приближаться к какому-то числу или вообще не проявлять какой-либо закономерности.
Определение 1.2. Число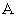 
называется пределом числовой последовательности , если для любого числа $IMAGE6$ существует такой номер числовой последовательности $IMAGE7$, зависящий от $IMAGE8$, что для всех номеров числовой последовательности $IMAGE9$ выполняется условие $IMAGE10$.
Последовательность, которая имеет предел, называется сходящейся. В этом случае пишут $IMAGE11$.
Очевидно, для выяснения вопроса о сходимости числовой последовательности необходимо иметь критерий, который был бы основан только на свойствах ее элементов.
Теорема 1.1. (теорема Коши о сходимости числовой последовательности). Для того, чтобы числовая последовательность была сходящейся, необходимо и достаточно, чтобы для любого числа $IMAGE6$ существовал такой номер числовой последовательности $IMAGE7$, зависящий от $IMAGE8$, что для любых двух номеров числовой последовательности $IMAGE15$ и $IMAGE16$, которые удовлетворяют условию $IMAGE9$ и $IMAGE18$, было бы справедливо неравенство $IMAGE19$.
Доказательство. Необходимость. Дано, что числовая последовательность сходится, значит, в соответствии с определением 2, у нее существует предел $IMAGE11$. Выберем какое-то число $IMAGE6$. Тогда, по определению предела числовой последовательности, существует такой ее номер $IMAGE7$, что для всех номеров $IMAGE9$ выполняется неравенство $IMAGE10$. Но так как $IMAGE8$ произвольно, то будет выполняться и $IMAGE27$. Возьмем два каких-то номера последовательности $IMAGE9$ и $IMAGE18$, тогда
$IMAGE30$.
Отсюда следует, что $IMAGE19$, то есть необходимость доказана.
Достаточность. Дано, что $IMAGE19$. Значит, существует такой номер $IMAGE7$, что для данного условия $IMAGE9$ и $IMAGE18$. В частности, если $IMAGE9$, а $IMAGE37$, то $IMAGE38$ или $IMAGE39$ при условии, что $IMAGE9$. Это значит, что числовая последовательность для $IMAGE42$ ограничена. Следовательно, по крайней мере, одна из ее подпоследовательностей $IMAGE43$ должна сходиться. Пусть $IMAGE44$. Докажем, что сходится к 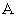также.
Возьмем произвольное $IMAGE6$. Тогда, согласно определению предела, существует такой номер $IMAGE48$, что для всех $IMAGE49$ выполняется неравенство $IMAGE50$. С другой стороны, по условию дано, что у последовательности существует такой номер $IMAGE7$, что для всех $IMAGE9$ и $IMAGE18$ будет выполняться условие $IMAGE55$.
Выберем $IMAGE56$ и зафиксируем некоторое $IMAGE57$. Тогда для всех $IMAGE9$ получим:
$IMAGE59$.
Отсюда следует, что $IMAGE11$, что и требовалось доказать.
Определение 1.3. Числовая последовательность называется монотонно возрастающей, если выполняется неравенство $IMAGE62$, и монотонно убывающей, если $IMAGE63$.
Теорема 1.2. Любая монотонно возрастающая ограниченная сверху числовая последовательность имеет предел.
Аналогичная теорема есть и для монотонно убывающей числовой последовательности.
2. Предел функции
При исследовании графиков различных функций можно видеть, что при неограниченном стремлении аргумента функции к какой-то величине, то ли конечной, то ли бесконечной, сама функция также может принимать ряд значений, неограниченно приближающихся к некоторой величине. Следовательно, для функции также можно ввести понятие предела.
Определение 2.1. Число 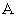называется пределом функции $IMAGE66$ в точке $IMAGE67$, если для любого $IMAGE6$ существует такое число $IMAGE69$, что из условия $IMAGE70$ следует, что $IMAGE71$.
Данное условие записывается в виде: $IMAGE72$. Отметим, что интервал длины $IMAGE73$, который содержит в себе точку $IMAGE67$, называется $IMAGE73$-окрестностью точки $IMAGE67$.
Аналогичным образом вводится понятие предела функции и при стремлении $IMAGE77$ к $IMAGE78$. Так же как и в случае числовой последовательности, для функции существует теорема Коши, которая определяет существование у нее предела.
Теорема Коши о существовании предела. Для того чтобы функция $IMAGE66$, где $IMAGE80$, имела предел 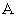при $IMAGE82$, где $IMAGE83$, необходимо и достаточно, чтобы для любого $IMAGE6$ существовало такое число $IMAGE69$, что из условия $IMAGE70$ вытекало условие $IMAGE71$.
Доказательства теоремы приводить не будем. В качестве предела функции могут служить как конечные, так и бесконечные величины.
Геометрический смысл теоремы Коши заключается в следующем. Возьмем некоторое $IMAGE73$, для которого $IMAGE70$. Тогда, согласно теореме, $IMAGE71$. Представим данное неравенство следующим образом: $IMAGE91$. Иначе говоря, как только $IMAGE77$ станет отличаться от $IMAGE67$ меньше, чем на $IMAGE73$, сама функция окажется в полосе шириной $IMAGE95$, расположенной на линии $IMAGE96$.
$IMAGE104$
В приведенном определении предела и теореме Коши $IMAGE77$ может стремиться к $IMAGE67$ произвольным образом. Однако во многих случаях это стремление происходит с какой-то одной стороны. Для этого вводятся понятия односторонних пределов.
Определение 2.2. Если $IMAGE77$ стремится к $IMAGE67$, оставаясь все время меньше его, и при этом $IMAGE66$ стремится к 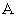, то это число называется пределом функции слева и обозначается $IMAGE111$.
Определение 2.3. Если $IMAGE77$ стремится к $IMAGE67$, оставаясь все время больше его, и при этом $IMAGE66$ стремится к 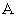, то это число называется пределом функции справа и обозначается $IMAGE116$.
Необходимо иметь в виду, что не всегда пределы слева и справа в точке $IMAGE67$ равны между собой.
3. Второй замечательный предел
Рассмотрим числовую последовательность $IMAGE118$, где $IMAGE119$, $IMAGE120$ С ростом $IMAGE121$ основание степени уменьшается до единицы, а показатель растет до бесконечности, поэтому ничего конкретного о поведении $IMAGE122$ сказать нельзя. Для вычисления $IMAGE123$ воспользуемся выражением для бинома Ньютона:
$IMAGE124$. (0.0.1)
В нашем случае
$IMAGE125$
$IMAGE126$.
Из полученного выражения следует, что с увеличением $IMAGE121$ величина $IMAGE128$ растет. Действительно, перейдем от $IMAGE121$ к $IMAGE130$. Это приведет к тому, что число слагаемых возрастет на одно. Кроме того, величина множителей, заключенных в скобки, тоже возрастет, так как $IMAGE131$. Но если увеличивается число слагаемых и сами слагаемые растут, то $IMAGE132$. Значит, числовая последовательность $IMAGE118$ монотонно возрастает.
Докажем теперь, что данная последовательность ограничена сверху. Заменим все скобки вида $IMAGE134$ единицей. Так как $IMAGE135$, то
$IMAGE136$.
Кроме того $IMAGE137$, $IMAGE138$,..., $IMAGE139$. Значит,
$IMAGE140$.
В правой части неравенства после цифры 2 стоит убывающая геометрическая прогрессия. Как известно, сумма $IMAGE121$ первых членов такой прогрессии равна: $IMAGE142$. В нашем случае $IMAGE143$. С ростом $IMAGE121$ величина $IMAGE145$ будет, очевидно, стремится к единице. Значит, $IMAGE146$, то есть, ограничено сверху.
Итак, мы получили, что $IMAGE147$. Но так как $IMAGE118$ монотонно возрастающая последовательность ограниченная сверху, то она имеет предел:
$IMAGE149$
Можно доказать, что данный предел справедлив не только для натуральных чисел, но и для любых значений $IMAGE150$:
$IMAGE151$.
Полученное выражение и называется вторым замечательным пределом.
Число $IMAGE152$ используется для введения натуральных логарифмов. Такие логарифмы обозначаются $IMAGE153$, при этом $IMAGE154$.
Следствие 3.1.
$IMAGE155$
$IMAGE156$.
В частности, если $IMAGE157$, то $IMAGE158$.
Следствие 3.2.
$IMAGE159$.
В частности, если $IMAGE157$, то $IMAGE161$.
4. Сравнение бесконечно малых величин
Как следует из определения бесконечно малых величин, все они стремятся к нулю, но скорость этого стремления может быть различна. Поэтому все бесконечно малые величины можно сравнивать между собой.
Пусть даны две бесконечно малые величины $IMAGE162$ и $IMAGE163$ при $IMAGE164$, то есть $IMAGE165$, $IMAGE166$.
Определение 4.1. Функции $IMAGE162$ и $IMAGE163$ называются бесконечно малыми величинами одного порядка малости, если $IMAGE169$.
Определение 4.4. Функция $IMAGE162$ называется бесконечно малой величиной более высокого порядка малости, чем $IMAGE163$, если $IMAGE172$.
Определение 4.3. Функция $IMAGE162$ называется бесконечно малой величиной более низкого порядка малости, чем $IMAGE163$, если $IMAGE175$.
Тот факт, что $IMAGE162$, например, имеет более высокий порядок малости, чем $IMAGE163$, можно обозначить следующим образом: $IMAGE178$.
Определение 4.4. Функция $IMAGE162$ называется бесконечно малой величиной $IMAGE180$го порядка малости относительно $IMAGE163$, если $IMAGE182$.
Определение 4.5. Функции $IMAGE162$ и $IMAGE163$ называются несравнимыми бесконечно малыми величинами, если $IMAGE185$ не существует и не равен $IMAGE186$.
Определение 4.6. Две бесконечно малые величины $IMAGE162$ и $IMAGE163$ называются эквивалентными, если $IMAGE189$.
Очевидно, что это частный случай бесконечно малых величин одного порядка малости. Эквивалентные величины обозначаются следующим образом: $IMAGE190$.
Понятие эквивалентности имеет практическое приложение. Если $IMAGE189$, то это значит, что при достаточном приближ