База рефератов

Міністерство освіти та науки України

Дніпропетровський національний університет

Механіко-математичний факультет

Кафедра диференційних рівнянь

Випускна робота

Побудова розв’язку задачі Гурса

для телеграфного рівняння методом Рімана

Виконав: студент гр. МЕ-97-2                 Керівник: проф. Остапенко В.О.

                  Коленкін О.О.                                

                                                                     “___” _________2001.______

Допущено до захисту:                               Рецензент:доц. Грішин В.Б.

Завідувач кафедрою Поляков М.В.                   

“___” _________2001._______                 “ ___” _________2001.______

Дніпропетровськ.

2001
Зміст.

Реферат................................................................................................... 4

The summary.......................................................................................... 5

Вступ....................................................................................................... 6

§1. Постановка задачі.......................................................................... 8

§2. Приведення до канонічного вигляду гіперболічного рівняння другого порядку з двома незалежними змінними. Характеристики............................. 9

§3. Формула Остроградського-Гаусса............................................. 12

§4. Існування та єдиність розв’язку задачі Гурса.......................... 13

§5. Спряжені диференційні оператори............................................. 19

§6. Побудова розв’язку...................................................................... 21

§7. Деякі приклади на знаходження фунції Рімана....................... 25

Висновок.............................................................................................. 31

Список використованої літератури:................................................ 32

Реферат

Сторінок: 31, рисунків: 2, джерел: 4.

Ключеві слова: рівняння гіперболічного типу, характеристики, задача Гурса, метод послідовних наближень, спряжений оператор, формула Гріна, функція Рімана.

Мета роботи: в даній роботі необхідно ознайомитись з методом отримання розв’язку задачі Гурса для телеграфного рівняння (1.1) з початковими умовами (1.2); довести існування та єдиність цього розв’язку; навести приклади та вказати області вживання цього методу у прикладних науках.

The summary.

In the given operation some questions, concerning equations in partial derivatives of the second order with two explanatory variables of hyperbolic type are considered. The algorithm of coercion to a canonical form of these equations is shown, definition of characteristics is given. The method of construction of solution of Gourses problem for the telegraphic equation is stated. Existence and uniqueness of solution of Gourses problem is proved. Some questions concerning of conjugate differential operators, in particular, are considered is obtained the important formula (Green's formula) on which usage Rimahn’s method leans. Auxiliary function (Rimahn’s function (6.4)) is entered. The number of examples on finding of this function is given.  
Вступ У світі, який нас оточує, відбувається багато різних процесів – фізичні, хімічні, біологічні та інші. Для вивчання цих процесів будують математичні моделі. Велика кількість задач зводиться до рівнянь у частинних похідних. Великий інтерес являє собою знаходження розв’яків для систем рівнянь, які підпорядковуються тим або іншим додатковим умовам. Ці додаткові умови, як правило, являють собою  задання невідомих функцій та деяких їхніх похідних на межі області, в якої шукається розв’язок, або складаються у тому, що невідомим функціям предписується той або інший характер властивості. В загальному випадку ці додаткові умови називаються граничними умовами. Задачі на відшукання розв’язків системи рівнянь у частинних похідних, підлеглих вказаним додатковим умовам, в загальному випадку називаються граничними задачами. Прикладом граничної задачі може бути задача Гурса. Граничні задачі Гурса використовують для описання процесів сорбції, десорбції, сушки, процесів каталітичних хімічних реакцій та деяких інших процесів.

Німецьким математиком Ріманом (17.09.1826 – 30.07.1866) був пропонований важливий метод інтегрування рівняння (1.1), який базується на використанні формули Гріна (5.2). Цей метод дозволяє виразити в явному вигляді шукаємий розв’язок задачі Гурса через граничні умови (1.2).

Робота складається з вступу, заключення та семи параграфів. Зробимо коротенький огляд кожного параграфу.

В §1 цієї роботи наведена постановка задачі Гурса. На рисунку 1 показана область D, в якій необхідно знайти розв’язок цієї задачі.

§2 присвячен деяким загальним питанням рівнянь у частинних похідних. Показан алгоритм приведення до канонічного вигляду гіперболічного рівняння у частинних похідних другого порядку з двома незалежними змінними. Дано означення характеристик.

§3 є допоміжним параграфом. У ньому наведено формулу  перетворення поверхневих інтегралів у об’ємні (3.2).

В §4 методом послідовних наближень доводиться існування та єдиність  розв’язку задачі Гурса.

§5 торкається питання спряжених диференційних операторів. Показано, що вираз vLu – uMv, де Mv – оператор, спряжений до Lu, можна зобразити як суму частинних похідних від деякіх виразів. Отримана формула Гріна (5.2).

§6 є основним параграфом в даній роботі. У ньому викладен метод Рімана. Шляхом введеня допоміжної функції (функції Рімана (6.4)) отримано розв’язок задачі Гурса у явному вигляді.

В §7 наведено деякі приклади знаходження функції Рімана.

 §1. Постановка задачі.

Нехай дано рівняння

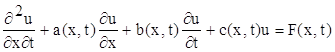                 (1.1)

Треба знайти розв’язок цього рівняння в області D(рис. 1)

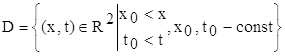
якщо задані крайові умови

u(x₀, t) = j(t);

 u(x, t₀) = y(x),                                          (1.2)

при цьому функції j(t) та y(x) ддиференцьовані, та задовільнюють умові спряження

j(t₀) = y(x₀).

Така задача називається задачею з даними на характкристиках, або задачею Гурса.

D

Рис. 1

§2. Приведення до канонічного вигляду гіперболічного рівняння другого порядку з двома незалежними змінними. Характеристики.

Розглянемо рівняння другого порядку з двома незалежними змінними

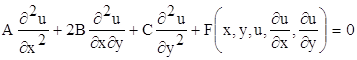,            (2.1)

де коефіцієнти А, В та С – функції від x та y, які мають неперервні похідні до другого порядку включно у області WÌ R. За допомогою перетворення змінних

x = j(х, у), h = y(х, у),

яке припускає обернене перетворення, ми отримуємо нове рівняння, еквівалентне рівнянню (2.1). При цьому будемо мати

$IMAGE6$

(2.2)

підставляючи значення похідних з(2.2) в (2.1), будемо мати:

$IMAGE7$,                           (2.3)

де

$IMAGE8$,

а функція $IMAGE9$ не залежить від других похідних. Замітимо, що якщо рівняння (2.1) було лінійно, то й рівняння (2.3) буде лінійним.

Рівняння (2.1) пов’язано з рівнянням:

Аdy²+2Вdydx+Сdx²=0                             (2.4)

яке має назву рівнянням характеристичних змінних, а його інтеграли – характеристиками для рівняння (2.1).

                                 (2.5)

Нехай j(x,y)=const є загальним інтегралом рівняння (2.4), тоді покладемо x=j(x,y) і коефіцієнт $IMAGE10$ буде дорівнювати нулю, якщо y(x,y)= const другий, відмінний від першого інтеграл, то заміною h=y(x,y) ми доб’ємось, щоб $IMAGE11$=0.

Як видно з формули (2.5), рівняння (2.4) може мати різні розв’язки, один розв’язок або не мати розв’язків взагалі в залежності від знаку В²–АС.

Рівняння (2.1) у деякій точці М(x,y) будемо називати:

1) рівнянням гіперболічного типу, якщо В²–АС>0;

2) рівнянням параболічного типу, якщо В²–АС=0;

3) рівнянням параболічного типу, якщо В²–АС<0.

Відмітимо, що при довільній заміні змінних (2.2) виконується рівність

$IMAGE12$

тобто при будь – якому перетворенні змінних, у якого якобіан відмінний від нуля, тип рівняння (2.1) не змінюється.

Розглянемо випадок, коли рівняння (2.1) має гіперболічний тип у деякій області GÌW. У цій області характеристичне рівняння має два різних загальних інтеграла j(x,y)=const та y(x,y)=const.

Зробимо заміну описану вище: x=j(x,y) та h=y(x,y), отримаємо:

$IMAGE13$

$IMAGE14$                         (2.6)

де $IMAGE15$

Рівняння (2.6) називається канонічною формою рівнянь гіпер-болічного типу. Покажемо, що характеристиками рівняння (2.6) будуть прямі, паралельні координатним осям, тобто x = const, h = const.

Для (2.6) рівнянням характеристичних змінних буде

dxdh = 0.

Звідки будемо мати

x = const, h = const.

§3. Формула Остроградського-Гаусса.

Нехай P(x, y, z), Q(x, y, z) и R(x, y, z) – три функциї змінних x, y, z, які задані у області D’ и мають в ній неперервні похідні першого порядку по x, по y та по z.

Розглянемо у D’ деяку замкнену поверхню S, яка складається з скінченного числа кусків з неперервно змінюючеюся на них дотичною площиною.

Таку поверхню називають кусочно-гладкою. Ми будемо, крім того, вважати, що прямі, паралельні координатним осям, зустрічають її або у скінченному числі точок, або мають загальним цілий відрізок.

Розглянемо інтеграл

$IMAGE16$,                       (3.1)

де через cos(nx), cos(ny), cos(nz) обозначені косінуси кутов, які  складені внутрішньою нормаллю до поверхні S з осями координат, а dS – додатній елемент поверхні. користуючись векторними позначеннями, ми можемо вважати P, Q, R компонентами деякого вектора, який позначимо літерою Т. Тоді

P cos(nx) + Q cos(ny) + Rcos(nz) = T_n,

де T_n – проєкція вектора Т на напрям внутрішньої нормалі.

Класична теорема з інтегрального счислення дозволяє перейти від поверхневого інтегралу (3.1) до об’ємного, расповсюдженого на область D, обмежену гладкою поверхнею S (яка задовольняє всім обмеженням, які було наведено вище). Ми будемо мати:

$IMAGE17$

або у векторних позначеннях

$IMAGE18$                                     (3.2)

где dv означає диференціал об’єму, а

$IMAGE19$.

Приведена нами формула справедлива у більш загальних припущеннях відносно S. Зокрема, формула (3.2) має місце для будь-якій кусочно – гладкої поверхні S, яка обмежує деяку область D.

§4. Існування та єдиність розв’язку задачі Гурса.

Розглянемо найпростішу задачу з даними на характеристиках

$IMAGE20$