База рефератов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Полуполя, являющиеся простыми расширениями с помощью комплексного числа

Выполнил

студент 5 курса

математического факультета

Чупраков Дмитрий Вячеславович

_____________________/подпись/

Научный руководитель:

д.ф-м.н., профессор Е.М. Вечтомов

_____________________/подпись/

Рецензент:

к.ф-м.н., доцент В.В. Чермных

_____________________/подпись/

Допущена к защите в ГАК

Зав. кафедрой ______________________д.ф-м.н., профессор Е.М. Вечтомов

                                      (подпись)                                “__” _________

Декан факультета _____________________к.ф-м.н., доцент В.И. Варанкина

                                      (подпись)                                “__” _________

Киров

2005

Содержание

Содержание. 2

Введение. 3

Глава 1. 5

1.1. Базовые понятия и факты.. 5

1.2. Простое расширение Q⁺(a) 5

1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел. 7

Глава 2. Однопорожденные полуполя. 9

2.1. Структура простого расширения полуполя неотрицательных рациональных чисел  9

2.2. Расширения полуполя неотрицательных действительных чисел комплексным числом. 11

2.3. Расширения полуполя неотрицательных рациональных чисел комплексным числом  12

2.4. Примеры.. 20

Литература. 22

Введение

Теория полуполей – одно из интенсивно развивающихся разделов общей алгебры, являющейся обобщением теории полей. Одним из основных способов исследования полей является построение их расширений. Поэтому естественно исследовать расширения полуполей. Эта проблема освещена в статье А.В.Ряттель [3] и диссертации И.И.Богданова. Но в них рассматриваются случаи упорядочиваемых расширений. Интересно рассмотреть неупорядочиваемые расширения. Этому вопросу посвящена данная квалификационная работа

Целью квалификационной работы является исследование однопорожденных расширений полуполей неотрицательных рациональных чисел и неотрицателных действительных чисел комплексным числом на предмет выявления признаков и свойств, позволяющих упростить поиск расширений, являющихся полуполями.

Выпускная квалификационная работа состоит из двух глав. В главе 1 представлены предварительные сведения, необходимые для изучения однопорожденных расширений полуполей. Глава 2 посвящена исследованию однопорожденных расширений полуполей.

В работе принята сквозная тройная нумерация теорем и лемм, где первое число – номер главы, второе – номер параграфа, третье – номер в параграфе. Например, теорема 2.1.1 – первая теорема первого параграфа второй главы.

Основными результатами работы являются:

· Теорема 2.2.1. Любое расширени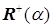е , где 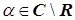, является полем С.

· Теорема 2.3.1. Если 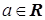, то 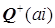 – поле тогда и только тогда, когда Q⁺(-a²) – поле, позволяющая выявлять полуполя вида .

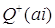· Теорема 2.3.6. Если минимальный многочлен f-g порождает полуполе то, он либо имеет положительный действительный корень, либо корень $IMAGE6$, такой что $IMAGE7$ и последовательность (**), заданная числами p и q, не содержит отрицательных элементов.
Последовательность    $IMAGE8$ задается следующим образом:

                $IMAGE9$

Эта теорема помогает сократить область поиска расширений, являющихся полуполями.

· Теорема 2.3.7. Для комплексных чисел $IMAGE10$ расширение $IMAGE11$, минимальное соотношение которого имеет положительный корень, является полуполем.

Глава 1.

1.1. Базовые понятия и факты

Определение: Алгебра <P, +, ×> называется полуполем, если

(1) <Р, +> – коммутативная полугруппа с 0;

(2) <Р, ×> – группа с 1;

(3) Дистрибутивность

a. $IMAGE12$

b. $IMAGE13$

(4) $IMAGE14$

Не сложно показать, что Q⁺ является полуполем.

Определение: Пусть Р – подполуполе полуполя F, $IMAGE15$, тогда простым расширением полуполя P с помощью элемента a называется наименьшее подполуполе полуполя F, содержащее множество P и элемент a. Простое расширение P с помощью a обозначается P(a).

1.2. Простое расширение Q⁺(a)

Теорема 1.2.1. Произвольное полутело либо аддитивно идемпотентно, либо содержит копию Q⁺ в качестве полутела.

Доказательство. Предположим, что S – неидемпотентное полутело, т.е. найдется такой ненулевой элемент sÎS, что s+s¹s. Откуда

$IMAGE16$.

Рассмотрим суммы единиц. Через $IMAGE17$ обозначим сумму k единиц (при kÎN). Так как любое полутело является антикольцом, то $IMAGE18$. Покажем, что суммы различного числа единиц в S различны. Допустим от противного, что $IMAGE19$ при некоторых натуральных m<n. Положим l=n-mÎN. Тогда $IMAGE20$. Прибавляя к обеим частям этого равенства элемент $IMAGE21$, получим

$IMAGE22$.

Применяя эту процедуру несколько раз, будем иметь

$IMAGE23$ для любого tÎN.

По свойству Архимеда, найдется такое tÎN, что tl>n. При k=tl имеем $IMAGE24$ и n<k. Тогда

$IMAGE25$.

Откуда 1=1+1 ( $IMAGE26$). Получили противоречие.

Следовательно, полутело S содержит аддитивную копию N. Но тогда S содержит и частные сумм 1, т.е. содержит копию полуполя Q⁺, причем, очевидно, операции в Q⁺ и S согласованы.

■

Теорема 1.2.2. $IMAGE27$- простое расширение полуполя Q⁺.

Доказательство. Заметим, что Q⁺(a) – полуполе. Кроме того, а Î Q⁺(a). Это не сложно увидеть, взяв $IMAGE28$. Очевидно $IMAGE29$.

Предположим, что есть полуполе P меньшее Q⁺(a), содержащее а и Q⁺. Тогда оно содержит все выражения вида $IMAGE30$. Так как P – полуполе, то $IMAGE31$. Таким образом, $IMAGE32$. Так как P – минимальное полуполе, то $IMAGE33$. То есть, $IMAGE34$–простое расширение полуполя Q⁺.

■

Аналогично доказывается следующее утверждение.

Теорема 1.2.3. $IMAGE35$- простое расширение поля Q.

1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел

Пусть а – алгебраическое число. Тогда минимальный многочлен F числа а имеет степень ≥ 1. Тогда обозначим через f многочлен, составленный из положительных одночленов многочлена F, а многочлен g составим из отрицательных членов, взятых с противоположными знаками. Тогда $IMAGE36$. $IMAGE37$, тогда $IMAGE38$.

Покажем, что любое равенство $IMAGE39$ получается из $IMAGE38$, где $IMAGE41$. Заметим, что $IMAGE42$, так как а – корень $IMAGE43$, а $IMAGE36$ – минимальный многочлен для a. Представим $IMAGE45$, где $IMAGE46$ составлен из положительных одночленов многочлена h, а $IMAGE47$ ‑ составлен из отрицательных одночленов многочлена h, взятых с противоположным знаком. Таким образом,

$IMAGE48$

Приведем подобные члены в паре $IMAGE43$, и найдем такой $IMAGE50$, что

$IMAGE51$,   $IMAGE52$

не имеют подобных членов.

Аналогично найдем $IMAGE53$, что

$IMAGE54$ и

$IMAGE55$ 

не имеют подобных членов.

Получаем

$IMAGE56$

Так как $IMAGE57$ не имеют подобных членов и $IMAGE58$ не имеют подобных членов, то

$IMAGE59$,    $IMAGE60$ или

$IMAGE61$, $IMAGE62$.

Найдем значения этих многочленов в точке а.

$IMAGE63$, $IMAGE64$.

Итак,

$IMAGE65$,

$IMAGE66$.

То есть, $IMAGE67$ тогда и только тогда, когда $IMAGE68$.

Будем говорить, что Q⁺(a) порождается минимальным соотношением $IMAGE68$.

Глава 2. Однопорожденные полуполя

2.1. Структура простого расширения полуполя неотрицательных рациональных чисел

Для простого расширения $IMAGE34$ справедливы следующие теоремы.

Теорема 2.1.1. Пусть $IMAGE34$ простое расширение $IMAGE72$, a – алгебраический элемент над $IMAGE72$. Тогда эквивалентны следующие утверждения:

(1) $IMAGE34$ – поле;

(2) $IMAGE75$;

(3) $IMAGE76$;

(4) $IMAGE77$;

(5) $IMAGE78$.

Доказательство.

· (1)®(2): Пусть $IMAGE34$ – поле. Так как $IMAGE80$ - простое расширение поля Q элементом a. То $IMAGE81$. Однако, $IMAGE82$. Таким образом, $IMAGE75$.

· (2)®(3): Заметим, что достаточно показать, что

$IMAGE84$.

Пусть его нет, тогда покажем, что никакой ненулевой элемент $IMAGE85$ не будет обратим. Рассмотрим

$IMAGE86$ и

$IMAGE87$,

тогда

$IMAGE88$.

По предположению, этот многочлен – тождественный ноль. А значит. $IMAGE89$. Так как $IMAGE90$, то $IMAGE91$. То есть, оба многочлена – нулевые. Мы же брали ненулевой многочлен b. Это показывает справедливость (3).

· (3)®(4): Пусть $IMAGE76$, тогда $IMAGE93$. Так как (f – g)(a) = 0, то h(a) = 0.

· (4)®(5): Пусть $IMAGE84$, покажем, что $IMAGE95$.

Так как h(a)=0, то $IMAGE96$. Покажем, что $IMAGE78$. Рассмотрим

$IMAGE98$.

Если b₀≠0, то

$IMAGE99$.

Если h₀=0, то

$IMAGE100$.

Так как a≠0, то

$IMAGE101$.

Тогда

$IMAGE102$.

Итак, $IMAGE78$.

· (5)®(1): Пусть $IMAGE78$, покажем, что Q⁺(a) – поле. Действительно, мы знаем, что Q⁺(a) – полуполе. Рассмотрим bÎQ⁺(a), тогда $IMAGE105$. b + (‑b)=0. То есть, Q⁺(a) – поле.

Итак, мы показали, что все утверждения равносильны.                                ■

Доказанный факт влечет следующую теорему.

Теорема 2.1.2. Пусть Q⁺(a) простое расширение Q⁺, a – алгебраический элемент над Q⁺. Тогда эквивалентны следующие утверждения:

(1) Q⁺(a) –полуполе;

(2) $IMAGE106$;

(3) $IMAGE107$;

(4) $IMAGE108$;

(5) $IMAGE109$.

Доказательство. Несложно установить равносильность утверждений (1) ‑ (4), исходя из предыдущей теоремы. Докажем условие равносильность их утверждению (5).

Из условия (5) следует, что никакой элемент не обратим по сложению. Тогда Q⁺(a) не является полем, а значит Q⁺(a) – полуполе. Докажем, что из (3) следует (5). Действительно, согласно условию (3),

("hÎQ⁺[a], h≠0) h(a)≠0.

То есть, если h(a)=0, то h=0. Пусть h(a)=(x+y)(a)=0. Тогда

$IMAGE110$.

Тогда (x_i+y_i)=0.

Так как x_iÎQ⁺ и y_iÎQ⁺, то x_i=y_i=0. А значит, x=y=0.

Теорема доказана.

■

2.2. Расширения полуполя неотрицательных действительных чисел комплексным числом

Теорема 2.2.1. Любое расширени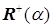е , где 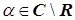, является полем С.

Доказательство. Пусть $IMAGE113$, $IMAGE114$