Описываются понятия r-перестановок множества, r-сочетания, перестановки с повторениями.
п.1. r- перестановки.
Определение. r- перестановкой множества A называется кортеж из r попарно различных элементов множества A. Иногда r- перестановки называют размещениями без повторения.
Если (a 
, ..., a 
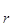) есть r- перестановка n- элементного множества, то r £ n.
Обозначение. Обозначим P(n, r) число всех r- перестановок n- элементного множества, где n, rÎN. Положим P(n, 0) = 1 для nÎN0.
Теорема 1. Число всех r- перестановок n- элементного множества, где
n, rÎN, вычисляется по формуле
P(n, r) = n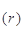 
= n(n -1)...(n - r + 1). (1)
Доказательство. Первая координата r- перестановки n- элементного множества может быть выбрана n способами, если первая координата выбрана, то вторая координата может быть выбрана n-1 способами, если выбраны первые две координаты, то третья координата может быть выбрана n-2 способами и т.д. до r- ой координаты включительно, которая может быть выбрана n-r+1 способами. Из теоремы 2, п.3, следует равенство (1).
Следствие 1. Пусть A и B- конечные множества, |A| = n, |B| = r, где
n, r ÎN. Тогда число всех инъекций f: B ® A равно P(n, r) = n .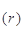
Доказательство. Обозначим B={b , ..., b 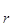}, инъекция f: B ®A может быть записана в табличной форме
$IMAGE7$,
где кортеж $IMAGE8$есть r- перестановка множества A. Поэтому искомое число равно P(n, r).
Определение. Пусть A есть n- элементное множество. Перестановкой множества A называется n- перестановка множества A. Другими словами, перестановка множества A это кортеж содержащий все элементы множества A по одному разу.
Следствие 2. Число всех перестановок n- элементного множества равно n!.
Доказательство. Искомое число равно P(n, n) = n $IMAGE9$= n(n-1)...(n-n+1) =
= n!.
Следствие 3. Пусть A и B- конечные множества, |A| = |B| = n, nÎN. Тогда число всех биекций f: B ® A равно n!.
Доказательство. Т.к. |A| = |B|, то каждая биекция f: B ® A является инъекцией и наоборот. По следствию 1, искомое число равно P(n, n) = n!.
п.2. r -элементные подмножества (r - сочетания).
Определение. Пусть A- конечное множество. r- сочетанием множества A называется любое r- элементное подмножество множества A.
Теорема 1. Пусть A есть n- элементное множество, n, rÎN $IMAGE10$. Справедливы утверждения:
1. Число всех r- сочетаний n- элементного множества равно $IMAGE11$.
2. Число всех r- элементных подмножеств n- элементного множества равно $IMAGE12$.
Доказательство. Обозначим K- число всех r- сочетаний n- элементного множества A. Каждое r- элементное подмножество n- элементного множества A определяет r! перестановок множества A, при этом разные подмножества определяют разные перестановки. Поэтому K×r! - число всех r- перестановок множества A, равное n 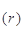. Отсюда следует, что K = n 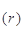/ r! = = $IMAGE12$.
Пример 1. Каждый кортеж $IMAGE16$N $IMAGE17$, где $IMAGE18$, кодируется k-элементным подмножеством $IMAGE19$ множества $IMAGE20$. Поэтому, при фиксированном k, число всех кортежей $IMAGE16$N $IMAGE17$, где $IMAGE18$, равно $IMAGE24$.
Пример 2. Перечисление беспорядков степени n. Обозначим U- множество всех перестановок степени n, $IMAGE25$. Будем считать, что элементами перестановок являются числа $IMAGE20$. Перестановка $IMAGE27$ степени n называется беспорядком, если $IMAGE28$ для всех $IMAGE29$.
Существует только один беспорядок $IMAGE30$ степени 2.
Существует только два беспорядка $IMAGE31$ степени 3.
Для $IMAGE29$ обозначим $IMAGE33$ множество всех $IMAGE27$ перестановок степени n таких, что $IMAGE35$. Число всех беспорядков степени n равно числу всех перестановок степени n не принадлежащих множеству $IMAGE36$. Обозначим $IMAGE37$ число всех беспорядков степени n. По формуле включения- исключения
$IMAGE38$, (1)
где суммирование ведётся по всем кортежам $IMAGE16$N $IMAGE17$таким, что
$IMAGE18$. Легко видеть, что для любого кортежа $IMAGE16$ N $IMAGE17$, где $IMAGE18$ справедливо равенство
$IMAGE45$.
При фиксированном k число всех кортежей $IMAGE16$N $IMAGE17$, где $IMAGE18$, равно $IMAGE24$. Из равенства (1) следует, что
$IMAGE50$.
Поэтому
$IMAGE51$.
п.3. Перестановки с повторениями.
Определение. Кортеж t = (b , ..., b $IMAGE53$) называется перестановкой с повторениями состава (n , ..., n $IMAGE55$) множества {a , ..., a $IMAGE55$}, если элемент a входит в t n раз, ..., a $IMAGE55$ входит в t n $IMAGE55$ раз, где n , ..., n $IMAGE55$ÎN $IMAGE10$, $IMAGE65$.
Обозначение. Обозначим P(n , ..., n $IMAGE55$) число всех перестановок с повторениями состава (n , ..., n $IMAGE55$) некоторого k - элементного множества, где n = = n +...+n $IMAGE55$.
Теорема 1. Для любого (n , ..., n $IMAGE55$)ÎN $IMAGE74$
P(n , ..., n $IMAGE55$) = n!/n !...n $IMAGE55$! , где n = n +...+n $IMAGE55$ .
Доказательство. Перестановка (b , ..., b $IMAGE53$) состава (n , ..., n $IMAGE55$) множества {a , ..., a $IMAGE55$} кодируется кортежем длины k: на первом месте кортежа записано множество тех мест в перестановке на которых расположен элемент $IMAGE87$; на втором месте кортежа записано множество тех мест в перестановке, на которых расположен элемент $IMAGE88$; ...; на k - ом месте кортежа записано множество тех мест в перестановке, на которых расположен элемент $IMAGE89$. Первый элемент кортежа может быть выбран $IMAGE90$ способами; если первый элемент выбран, то второй можно выбрать $IMAGE91$способами; ...; если первые $IMAGE92$ элементов выбраны, то k- ый элемент может быть выбран $IMAGE93$способами. По правилу произведения получаем, что число всех перестановок с повторениями состава (n , ..., n $IMAGE55$) из {a , ..., a $IMAGE55$} равно
P(n , ..., n $IMAGE55$) = $IMAGE100$ $IMAGE91$... $IMAGE102$=
= $IMAGE103$
Обозначение. Для " n , ..., n $IMAGE55$ÎN $IMAGE10$ полиномиальный коэффициент $IMAGE107$определяется равенствами:
если n +...+ n $IMAGE55$ = n, то $IMAGE110$ ;
если n +...+ n $IMAGE55$ ¹ n, то $IMAGE113$ .
Следствие 1. Пусть A и B- конечные множества такие, что |A| = n, |B| = k, (n , ..., n $IMAGE55$)ÎN $IMAGE74$, n +...+ n $IMAGE55$ = n, B = {b , ..., b $IMAGE55$}. Тогда число всех функций
f: A ® B таких, что |f $IMAGE121$(b $IMAGE122$)| = n $IMAGE122$ для всех i = 1, ..., k, равно $IMAGE107$.
Доказательство. Пусть A={a , ..., a $IMAGE53$}. Запишем функцию f: A ® B в табличном виде $IMAGE127$.
Кортеж (f(a ), ..., f(a $IMAGE53$)) есть перестановка с повторениями состава (n , ..., n $IMAGE55$) множества {b , ..., b $IMAGE55$}.
Следствие 2. Пусть U- конечное множество, |U| = n. Тогда число кортежей множеств (A , ..., A $IMAGE55$) таких, что
|A | = n , ..., |A $IMAGE55$| = n $IMAGE55$,
|A $IMAGE122$ÇA $IMAGE141$| = Æ для всех i ¹ j,
A È...ÈA $IMAGE55$ = U, равно $IMAGE107$.
Доказательство. По теореме 2 п.3 число таких кортежей равно
$IMAGE145$ $IMAGE91$... $IMAGE147$= $IMAGE107$.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/