Міністерство освіти і науки України
Дніпропетровський національний університет ім. Олеся Гончара
КОНТРОЛЬНА РОБОТА
з дисципліни „Диференціальні рівняння"
на тему „Особливі точки”
Виконавець: студентка групи
Назаренко Олеся
Перевірив:
м. Дніпропетровськ 2010 р.
Зміст
1. Особливі точки
2. Задача 1
3. Задача 2
4. Задача 3.
5. Задача 4
Особливою точкою системи
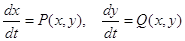(1)
або рівняння
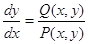(2)
де функції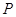 
й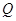 
неперервно диференційовані, називається така точка, в якій 
.
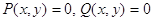Для дослідження особливої точки системи
$IMAGE6$ (3)
або рівняння
$IMAGE7$ (4)
треба знайти розв’язок характеристичного рівняння
$IMAGE8$ (5)
Якщо розв’язки $IMAGE9$ дійсні, різні $IMAGE10$ й одного знаку $IMAGE11$, то особлива точка - вузол (рис.1, а), причому стійкий, якщо $IMAGE12$ й нестійкий, якщо $IMAGE13$.
Вузол характеризується тим, що всі траєкторії, крім однієї II, мають у точці (0,0) загальну дотичну I, що сама є траєкторією. Прямі I і II спрямовані вздовж власних векторів матриці $IMAGE14$, які відповідають $IMAGE15$ і $IMAGE16$, причому пряма I відповідає меншому за модулем з $IMAGE15$ і $IMAGE16$.
При $IMAGE12$ вузол є стійкою точкою спокою. На рис.1а стрілками показаний напрямок руху вздовж траєкторії при зростанні $IMAGE20$ у випадку стійкого вузла. Якщо $IMAGE13$, то вузол нестійкий і стрілки заміняються на протилежні.
$IMAGE22$
Рис.1. Типові траєкторії [2]
Якщо розв’язки $IMAGE9$ дійсні, різні $IMAGE10$ й різних знаків $IMAGE25$, то особлива точка - сідло (рис.1, б). Сідло є нестійкою точкою спокою.
Сідло характеризується наявністю двох траєкторій I і II, що проходять через (0,0) також у напрямку власних векторів. Пряма I є асимптотою для інших траєкторій при $IMAGE26$, а II є асимптотою при $IMAGE27$. Прямолінійна траєкторія I розташована за напрямком власного вектора, що відповідає додатньому $IMAGE28$, а прямолінійна траєкторія II за напрямком власного вектора, що відповідає від‘ємному $IMAGE28$. Прямі I і II називаються сепаратрисами сідла. На рис.1б стрілками показаний напрямок руху вздовж траєкторії при зростанні $IMAGE20$. Сепаратриса II є єдиною траєкторією, якій відповідає розв’язок, що прямує до 0 при $IMAGE26$. Тільки дві траєкторії I і II є прямолінійними. Інші траєкторії криволінійні й зі зростанням $IMAGE20$ йдуть із $IMAGE33$ в $IMAGE33$. Сепаратриси I і II розділяють фазову площину на 4 області, у яких лежать криволінійні траєкторії.
Якщо розв’язки $IMAGE35$ комплексні з дійсною частиною $IMAGE36$, відмінною від нуля, то особлива точка - фокус (рис.1, в), причому стійкий, якщо $IMAGE37$ й нестійкий, якщо $IMAGE38$. На рис.1в стрілками показаний напрямок руху при зростанні $IMAGE20$ у випадку стійкого фокуса.
Зауваження. У випадку фокуса траєкторії можуть бути закручені навколо (0,0) у різних напрямках. Для того, щоб визначити напрямок закручування, досить обчислити вектор швидкості $IMAGE40$ в якій-небудь точці, наприклад, в (0,1). Аналогічно досліджується напрямок руху у випадку центра й виродженого вузла.
Якщо розв’язки $IMAGE35$ комплексні чисто мнимі ( $IMAGE42$), то особлива точка - центр (рис.1, г). Центр є стійкою, але не асимптотично стійкою точкою спокою.
Якщо розв’язки рівні й ненульові (тобто $IMAGE43$), то особлива точка може бути виродженим вузлом (рис.1, д) або дикритичним вузлом (рис.1, е), причому дикритичний вузол має місце тільки у випадку системи $IMAGE44$ (або рівняння $IMAGE45$), а у всіх інших випадках при $IMAGE43$ особлива точка є виродженим вузлом. У випадку виродженого вузла всі траєкторії дотикаються однієї прямої, спрямованої вздовж єдиного власного вектора, що відповідає $IMAGE28$. Дикритичний вузол може бути стійким $IMAGE48$ і нестійким $IMAGE49$.
Якщо ж один або обидва розв’язки рівняння (5) дорівнюють нулю, то $IMAGE50$, і, отже, дріб у правій частині рівняння (4) скорочується. Рівняння набуває вигляду $IMAGE51$, і розв’язок на площині XOY зображуються паралельними прямими.
Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:
$IMAGE52$
Розв’язання.
Для дослідження особливої точки рівняння
$IMAGE7$
треба знайти розв’язок характеристичного рівняння
$IMAGE8$
У нас $IMAGE55$, $IMAGE56$, $IMAGE57$, $IMAGE58$. Складаємо характеристичне рівняння
$IMAGE59$
і розв’язуємо його відносно $IMAGE28$
$IMAGE61$
Розв’язки характеристичного рівняння дійсні й мають різні знаки.
Отже, особлива точка (0,0) - сідло. Сідло є нестійкою точкою спокою.
1. Перший спосіб побудови інтегральних кривих.
Власний вектор $IMAGE62$, що відповідає власному числу $IMAGE15$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE65$. Маємо
$IMAGE66$
$IMAGE67$
$IMAGE68$
Власний вектор (1; 1/2) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE69$.
Далі, власний вектор $IMAGE62$, що відповідає власному числу $IMAGE16$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE73$. Маємо
$IMAGE66$
$IMAGE75$
$IMAGE76$
Власний вектор (1; - 1) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE77$.
На площині $IMAGE78$ будуємо прямі, спрямовані вздовж власних векторів (1; 1/2) і (1; - 1), а потім будуємо гіперболи.
2. Другий спосіб побудови інтегральних кривих.
Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол).
Прямі, що проходять через особливу точку (0,0), шукаємо у вигляді $IMAGE79$. Підставляючи $IMAGE79$ у вихідне рівняння
$IMAGE81$,
одержуємо рівняння для визначення коефіцієнта $IMAGE82$
$IMAGE83$
$IMAGE84$
$IMAGE85$
$IMAGE86$
$IMAGE87$
Таким чином, маємо дві шукані прямі
$IMAGE88$, $IMAGE89$.
3. Напрямок руху по траєкторіях. Для з'ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці $IMAGE90$ вектор швидкості $IMAGE91$. Наприклад, у точках $IMAGE92$ та $IMAGE93$вектор швидкості дорівнює
$IMAGE94$, $IMAGE95$,
у точках $IMAGE96$ та $IMAGE97$вектор швидкості дорівнює
$IMAGE98$, $IMAGE99$,
у точках $IMAGE100$ та $IMAGE101$ вектор швидкості дорівнює
$IMAGE102$, $IMAGE103$,
у точках $IMAGE104$ та $IMAGE105$ вектор швидкості дорівнює
$IMAGE106$, $IMAGE107$.
Приблизний вид сім’ї інтегральних кривих зображено на рисунку 2.
$IMAGE108$
Рис.2. Положення рівноваги й інтегральні криві [6]
Дослідити особливі точки рівняння. Накреслити інтегральні криві на площині XOY:
$IMAGE109$
Розв’язання. Для дослідження особливої точки рівняння
$IMAGE7$
треба знайти розв’язок характеристичного рівняння
$IMAGE8$
У нас $IMAGE112$, $IMAGE113$, $IMAGE114$, $IMAGE115$. Складаємо характеристичне рівняння
$IMAGE116$
і розв’язуємо його відносно $IMAGE28$
$IMAGE118$
Розв’язки характеристичного рівняння дійсні, різні й одного знака.
Отже, особлива точка (0,0) - стійкий вузол ( $IMAGE12$).
1. Перший спосіб побудови інтегральних кривих.
Власний вектор $IMAGE62$, що відповідає власному числу $IMAGE15$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE123$.
$IMAGE124$
$IMAGE125$
Власний вектор (2;
1) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE126$.
Далі, власний вектор $IMAGE62$, що відповідає власному числу $IMAGE16$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE130$.
$IMAGE124$
$IMAGE132$
Власний вектор (1; - 1) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE133$.
На площині $IMAGE78$ будуємо прямі, спрямовані вздовж власних векторів (2;
1) і (1; - 1), а потім будуємо параболи й вказуємо напрямок руху по траєкторіях.
2. Другий спосіб побудови інтегральних кривих.
Прямі, що містять фазові криві системи, шукаємо у вигляді $IMAGE79$.
Підставляючи $IMAGE79$ у вихідне рівняння
$IMAGE137$,
одержуємо рівняння для визначення коефіцієнта $IMAGE82$:
$IMAGE139$
$IMAGE140$
$IMAGE141$
Виходить, що $IMAGE142$ і $IMAGE143$ - шукані прямі.
Фазові криві - частини парабол, що дотикаються на початку координат прямої $IMAGE143$. Параболи дотикаються саме прямої $IMAGE143$, оскільки власний вектор (2;
1) матриці коефіцієнтів даної системи, що відповідає власному числу $IMAGE126$, паралельний прямій $IMAGE143$.
3. Напрямок руху по траєкторіях.
Для з'ясування напрямку руху по траєкторіях досить побудувати в якій-небудь точці $IMAGE90$ вектор швидкості $IMAGE149$. Наприклад, у точці $IMAGE150$ вектор швидкості дорівнює
$IMAGE151$,
а в точці $IMAGE152$ вектор швидкості
$IMAGE153$.
Приблизний вигляд сім’ї фазових кривих зображений на рисунку 3.
$IMAGE154$
Рис.3. Положення рівноваги й інтегральні криві [6]
Дослідити особливі точки системи. Накреслити інтегральні криві на площині XOY:
$IMAGE155$
Розв’язання.
Для дослідження особливої точки системи
$IMAGE6$
треба знайти розв’язок характеристичного рівняння
$IMAGE8$
У нас $IMAGE158$, $IMAGE159$, $IMAGE160$, $IMAGE161$. Складаємо характеристичне рівняння
$IMAGE162$
і розв’язуємо його відносно $IMAGE28$
$IMAGE164$
$IMAGE165$
$IMAGE166$
$IMAGE167$
Розв’язки характеристичного рівняння комплексні й різні.
Отже, особлива точка (0,0) - стійкий фокус ( $IMAGE168$).
Напрямок руху по траєкторіях.
Для з'ясування напрямку закручування інтегральних кривих (спіралей) будуємо вектор швидкості $IMAGE40$ в точці (1,0):
$IMAGE170$
Отже, спаданню $IMAGE20$ відповідає рух по спіралях за ходом годинникової стрілки. При русі за ходом годинникової стрілки інтегральні криві наближаються до початку координат (0,0).
Приблизний вигляд сім’ї інтегральних кривих зображено на рисунку 4.
$IMAGE172$
Рис.4. Положення рівноваги й інтегральні криві [6]
Дослідити особливі точки системи. Накреслити інтегральні криві на площині XOY:
$IMAGE173$
Розв’язання.
Для дослідження особливої точки системи
$IMAGE6$
треба знайти розв’язок характеристичного рівняння
$IMAGE8$
У нас $IMAGE176$, $IMAGE177$, $IMAGE57$, $IMAGE179$. Складаємо характеристичне рівняння
$IMAGE180$
і розв’язуємо його відносно $IMAGE28$
$IMAGE182$
Розв’язки характеристичного рівняння дійсні й мають різні знаки. Отже, особлива точка (0, 0) - сідло. Сідло є нестійкою точкою спокою.
1. Перший спосіб побудови інтегральних кривих.
Власний вектор $IMAGE62$, що відповідає власному числу $IMAGE15$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE186$. Маємо
$IMAGE187$
$IMAGE188$
$IMAGE189$
$IMAGE190$
Власний вектор (1,1) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE191$.
Власний вектор $IMAGE62$, що відповідає власному числу $IMAGE16$, знаходимо, підставляючи в рівняння
$IMAGE64$
значення $IMAGE73$. Маємо
$IMAGE196$
Власний вектор (0, $IMAGE197$) матриці коефіцієнтів даної системи, відповідає власному числу $IMAGE77$.
На площині $IMAGE78$ будуємо прямі, спрямовані вздовж власних векторів (1;
1) і (0, $IMAGE197$), а потім будуємо гіперболи.
2. Другий спосіб побудови інтегральних кривих.
Знайдемо сепаратриси сідла, тобто прямі, що розділяють гіперболи різних типів, які є фазовими кривими системи (тобто асимптоти цих гіпербол). Розділивши друге рівняння вихідної системи на перше рівняння, одержуємо
$IMAGE201$ або $IMAGE202$
Прямі, що проходять через особливу точку (0,0) ш