Содержание
Двойные интегралы
Определение определенного интеграла
Правило вычисления двойного интеграла.
Вычисление объемов тел с помощью двойного интеграла
Вычисление площадей поверхностей фигур с помощью двойного интеграла.
Тройные интегралы
Вычисление объемов тел с помощью тройного интеграла.
Несобственные интегралы.
Дифференциальные уравнения.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными
2. Однородные дифференциальные уравнения первого порядка
3. Линейные дифференциальные уравнения
4. Уравнения Бернулли
Дифференциальные уравнения второго порядка.
Три случая понижения порядка.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Комплексные числа
Геометрическое изображение комплексных чисел
Действия над комплексными числами.
Произведение.
Частное.
Возведение в степень.
Извлечение корня
Ряды.
Числовые ряды.
Свойства числовых рядов.
Знакоположительные ряды
Признаки сходимости и расходимости знакоположительных рядов.
Знакопеременные и знакочередующиеся ряды.
ДВОЙНЫЕ ИНТЕГРАЛЫ
Определение определенного интеграла
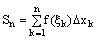- интегральная сумма.
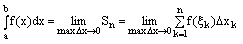
Геометрический смысл ОИ: равен площади криволинейной трапеции.
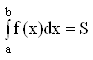
Аналогично ОИ выводится и двойной интеграл.
Пусть задана функция двух переменных z=f(x,y), которая определена в замкнутой области S плоскости ХОУ.
Интегральной суммой для этой функции называется сумма
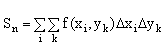
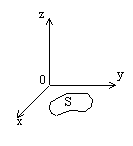
Она распространяется на те значения i и к, для которых точки (xi,yk) принадлежат области S.
Двойной интеграл от функции z=f(x,y), определенной в замкнутой области S плоскости ХОУ, называется предел соответствующей интегральной суммы.
$IMAGE6$
Правило вычисления двойного интеграла
Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.
$IMAGE7$
1. (Рис.1) Область интегрирования S ограничена прямыми х=а, х=в и кривыми
$IMAGE8$.
Для такой области двойной интеграл вычисляется через повторный по формуле:
$IMAGE9$
Сначала вычисляется внутренний интеграл:
При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.
2. (Рис.2) Область интегрирования S ограничена прямыми у=С, у=d и кривыми
$IMAGE10$.
Для такой области двойной интеграл вычисляется через повторный по формуле:
$IMAGE11$
Сначала вычисляется внутренний интеграл, затем внешний.
При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.
3. Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов.
Вычисление объемов тел с помощью двойного интеграла
$IMAGE12$
Объем тела, ограниченного сверху поверхностью z=f(x,y), снизу- плоскостью z=0 (плоскость ХОУ) и с боков- цилиндрической поверхностью, вырезающей на плоскости ХОУ область S, вычисляется по формуле:
$IMAGE13$
Вычисление площадей поверхностей фигур с помощью двойного интеграла
Если гладкая поверхность задана уравнением z=f(x,y), то площадь поверхности (Sпов.), имеющей своей проекцией на плоскость ХОУ область S, находится по формуле:
$IMAGE14$- площадь поверхности.
ТРОЙНЫЕ ИНТЕГРАЛЫ
Определяется аналогично двойному интегралу.
Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.
$IMAGE15$
Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) нтегралов.
Вычисление объемов тел с помощью тройного интеграла
Объем тела вычисляется по формуле:
$IMAGE16$
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Это интегралы: - с бесконечными пределами; - от неограниченной функции.
Первый вид
Несобственные интегралы с бесконечными пределами имеют вид:
$IMAGE17$; $IMAGE18$; $IMAGE19$
Несобственные интегралы от функции в пределах от (а) до ( $IMAGE20$) определяются равенством.
1. $IMAGE21$; 2. $IMAGE22$; 3. $IMAGE23$
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся (ряд сходится или расходится?). Это и есть ответ.
Второй вид
Несобственные интегралы от неограниченной функции имеют вид: $IMAGE24$, где существует точка “с” (точка разрыва) такая, что $IMAGE25$; $IMAGE26$, т.е. $IMAGE27$(в частности c=a; c=b).
Если функция f(x) имеет бесконечный разрыв в точке “с” отрезка [a;b] и непрерывна при $IMAGE28$или $IMAGE29$, то полагаем: $IMAGE30$
Если пределы в правой части последнего равенства существуют и конечны, то несобственный интеграл сходится, если пределы не существуют или равны бесконечности - то расходятся.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .
Символически дифференциальное уравнение выглядит:
F(x,y,y’,y’’…,y(n))=0 или $IMAGE31$.
2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение:
Пример.
F(x,y,y’)=0- дифференциальное уравнение первого порядка.
F(x,y,y’,y’’)=0- дифференциальное уравнение второго порядка.
3. Решением дифференциального уравнения называется всякая функция $IMAGE32$, которая при подстановке в уравнение, обращает его в верное тождество.
Для того чтобы решить дифференциальное уравнение надо его проинтегрировать.
Пример.
Дифференциальное уравнение первого порядка.
Общее и частное решения.
F(x,y,y’)=0
Это уравнение можно привести к виду y’=f(x,y).
Интегрируем уравнение.
После вычисления возникает постоянная С. Поэтому решение фактически зависит не только от х, но и от С, т.е. y=f(x,C). Придавая С различные значения, мы получаем множество различных решений дифференциального уравнения. Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.
Придавая С различные значения получаем различные решения дифференциального уравнения. Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество (которые отличаются друг от друга путем сдвига на несколько единиц).
Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.
Частное решение.
Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: а). у=у0 при х=х0; б). $IMAGE33$; в). у(х0)=у0.
Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.
Подставляя $IMAGE34$ в начальное условие $IMAGE33$, находим вполне определенные значения постоянной С. Тогда $IMAGE36$ является частным решением уравнения.
Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.
Теорема существования и единственности решения дифференциального уравнения (теорема Коши).
Если в дифференциальном уравнении y=f(x,y) функция f(x,y) и ее частная производная $IMAGE37$ определены и непрерывны в некоторой области Д на плоскости ХОУ, то какова бы ни была внутренняя точка (х0,у0) этой области, данное уравнение имеет единственное решение $IMAGE38$, удовлетворяющее начальному условию у=у0 при х=х0.
Геометрически смысл заключается в следующем: каждой точке (х0,у0) области Д соответствует только одна интегральная кривая, проходящая через эту точку (каждой точке соответствует только одно частное решение).
Замечание. “Найти частное решение”=“Решить задачу Коши”.
Существует 4 вида дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы
$IMAGE39$.
Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
- $IMAGE40$- через производную.
- $IMAGE41$- через дифференциал.
В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.
Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.
Решение.
- $IMAGE42$
$IMAGE43$; $IMAGE44$-интегрируем и получаем решение. $IMAGE45$
- $IMAGE46$
$IMAGE47$; $IMAGE48$
Однородные дифференциальные уравнения первого порядка
Функция f(x,y) называется однородной функцией n–го измерения, если при любом $IMAGE49$ выполняется условие: $IMAGE50$.
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy; $IMAGE51$
Однородное уравнение всегда можно привести к виду $IMAGE52$ и с помощью замены $IMAGE53$ однородное уравнение всегда приводится к уравнению с разделяющимися переменными ( $IMAGE53$; y=xt; y’=t+xt’).
Линейные дифференциальные уравнения
ЛДУ- уравнения вида y’+P(x)y=Q(x)– первого порядка относительно у и у’.
Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’
U’V+UV’+P(x)UV=Q(x)
V(U’+P(x)U)+UV’=Q(x)
Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными:
1). U’+P(x)U=0 находим U. $IMAGE55$ 2). UV’=Q(x) находим V. $IMAGE56$. С ставится только при вычислении второго уравнения.
Замечание. Выражение, стоящее в скобках, можно прировнять к нулю, т.к. одну из функций можно взять произвольной, другую – определяем на основании ЛДУ.
Уравнения Бернулли
УБ- дифференциальные уравнения вида y’+P(x)y=Q(x)*yn, где
$IMAGE57$- т.к. при этих значениях уравнение будет линейным.
УБ решаются так же, как и линейные.
Дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка в общем виде записываются: F(x,y,y’,y’’)=0
Как и в случае дифференциальных уравнений первого порядка для решения дифференциальных уравнений второго порядка существуют общее и частное решения. Но, если для дифференциальных уравнений первого порядка решение зависело от одной константы С, то для дифференциальных уравнений второго порядка решение зависит от двух постоянных: $IMAGE58$- общее решение.
Если заданы начальные условия (у=у0, у=у0 при х=х0), то получаем частное решение, удовлетворяющее этим начальным условиям.
Начальные условия так же могут задаваться в виде:
у=у0 при х=х0; у=у1 при х=х1.
Три случая понижения порядка
1. Случай непосредственного интегрирования
F(x,y”)=0
y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.
$IMAGE59$; $IMAGE60$; $IMAGE61$; $IMAGE62$
2. Когда дифференциальное уравнение явно не содержит у, т.е. F(x,y’,y”)=0
С помощью замены у’=р; $IMAGE63$ это уравнение приводим к уравнению первого порядка $IMAGE64$.
3. Когда диффер