База рефератов

Основные понятия алгебры множеств

Алгебра множеств лежит в основе многих разделов современной математики. Для нее практически невозможно установить точную дату открытия и назвать имя первооткрывателя. Алгебра множеств постепенно развивалась на фоне многочисленных попыток найти строгое математическое основание для Аристотелевой логики. Некоторые предпосылки этой алгебры содержатся в трудах Лейбница. В разработку основ этой алгебры внесли значительный вклад многие известные логики и математики (Ж.Д.Жергонн, А. де Морган, Дж. Венн и др.). Но особая заслуга в ее развитии и распространении принадлежит Леонарду Эйлеру.

В 1736 г. в "Письмах к германской принцессе о различных физических и философских материях" Л. Эйлер в популярной форме изложил свое понимание Аристотелевой силлогистики. При этом он использовал наглядные схемы, которые впоследствии получили название "круги Эйлера". В дальнейшем круги Эйлера стали использовать не только в учебных курсах по логике, но также и при изложении азов многих основополагающих разделов современной математики, в которых используется алгебра множеств. Здесь воспользуемся этими наглядными отображениями, позволяющими достаточно быстро овладеть абстрактными понятиями алгебры множеств.

Идеи Эйлера были развиты в работах французского астронома и математика Ж. Д. Жергонна. Жергонну удалось в опубликованной в 1817 г. работе "Основы рациональной диалектики" представить все классы суждений, выделенных Аристотелем, с помощью соотношений между множествами. Эти соотношения получили в математике и логике название "жергонновых отношений". Рассмотрим их более подробно.

В основе силлогистики лежат простые суждения, представленные четырьмя типами: A – общеутвердительное (все X есть Y); E – общеотрицательное (все X не есть Y); I – частноутвердительное (некоторые X есть Y); O – частноотрицательное (некоторые X не есть Y). Отметим, что в трудах Аристотеля смысл суждений отличается от общепринятого – этот смысл вместе с обозначениями утвердился в логике после работ известного схоласта Петра Испанского. Сам Аристотель не употреблял в суждениях двусмысленную связку "есть" и формулировал суждения следующим образом:

A: Y присуще всем X

E: Y не присуще всем X

I: Y присуще некоторым X

O: Y не присуще некоторым X

Термины X и Y можно представить как некоторые совокупности (множества, классы) в виде кругов Эйлера. Жергонн выделил 5 возможных соотношений между ними (рис. 1).

Рис. 1

Каждый тип Жергонновых отношений имеет собственное название:

G₁ – совпадение или равнозначность;

G₂ – левостороннее включение;

G₃ – частное совпадение;

G₄ – правостороннее включение;

G₅ – несовместимость.

Жергонн показал, что каждый тип Аристотелевского суждения соответствует некоторым типам этих отношений, в частности:

- типу A соответствует G₁ или G₂;

- типу E соответствует G₅;

- типу I: соответствует G₁ или G₂ или G₃ или G₄;

- типу O: соответствует G₃ или G₄ или G₅.

Например, суждение типа I означает, что некоторая непустая часть множества или класса X содержится в Y. Посмотрев на рисунок, нетрудно убедиться, что этому условию удовлетворяют все типы Жергонновых отношений кроме G₅. В логике слово "некоторые" используется в широком смысле: "хотя бы один, но не исключено, что и все". Жергонновы отношения часто использовались для строгого обоснования не только правил вывода для простого категорического силлогизма, в котором в качестве посылок используются только два суждения, но и для более сложных умозаключений, когда в качестве посылок допускается произвольное число суждений. Вершиной анализа такого рода можно считать работы английского логика и философа Дж. Венна (1834–1923).

Однако применение жергонновых отношений в логике связано с рядом трудностей. Главной из них является то, что практически для всех типов суждений (за исключением типа E) можно использовать несколько вариантов Жергонновых отношений, и при увеличении количества исходных суждений число возможных вариантов анализа возрастает в степенной зависимости. Если допустим, рассматриваем сложное рассуждение, содержащее много суждений, то должны для каждого суждения просмотреть все соответствующие ему варианты Жергонновых отношений. Однако работы Эйлера, Жергонна, Венна и многих других стали своеобразной "затравкой" для создания алгебры множеств.

С точки зрения современной математики алгебра множеств относится к классу алгебраических систем, т.е. структур, в которых имеются (даны):

1) носитель – некоторая совокупность объектов (например, числа, геометрические фигуры, слова, множества и т.д.);

2) совокупность отношений (например, больше, меньше, равно и т.д);

3) совокупность операций (например, сложение, умножение, пересечение и т. д).

Заметим, что смысловая разница между отношением и операцией заключается в следующем: если задано некоторое отношение между объектами, то о нем можно только сказать, истинно оно для данных объектов или нет (например, "2 > 3" является ложным отношением), в то время как в результате некоторой операции с объектами получается некоторый новый объект (например, "2+3=5").

В алгебре множеств носителем является некоторая совокупность множеств. Основными понятиями алгебры множеств считаются понятия множество и элемент. Соотношение между ними называется отношением принадлежности и обозначается знаком "Î". Запись

bÎA

переводится с символического языка как "bявляется элементом множества A" или "элемент b принадлежит множеству A". Если известны все элементы множества (например, a, b и c), то общепринятой является такая запись множества:

A={a,b,c}.

В этом случае элементы множества принято заключать в фигурные скобки. Кроме того, при перечислении элементов порядок несущественен, т.е. A={a,b,c}={c,b,a}={a,c,b} и т.д.

Множества могут быть заданы двумя способами: с помощью формулировки характерных признаков (например, множество K цифр, обозначающих четные числа) или с помощью перечисления элементов (например, K = {0, 2, 4, 6, 8})

В современной математике пока что нет четкого определения отношения принадлежности. В алгебре множеств этой неопределенности можно избежать, если считать, что это отношение связывает два разных типа объектов ("элемент"Î"множество"), но ни в коем случае не должно быть связи типа "множество"Î"множество".

Между множествами устанавливается другое вроде бы похожее, но в то же время принципиально отличающееся отношение – включение, структурные свойства которого в современной математике определены достаточно четко и однозначно. Рассмотрим его более подробно. Допускаются два отличающихся варианта этого отношения:

"Ì" – строго включено;

"Í" – включено или равно.

Запись AÌB означает, что множество A включено в множество B, т.е. все элементы множества A являются одновременно элементами множества B, но при этом невозможно равенство этих множеств. Запись AÍB означает, что множество A включено в множество B, но при этом не исключается, что они могут быть равными. Изображение отношения включения с помощью кругов Эйлера показано на рисунке 2. В данном случае не обязательно использовать правильные круги. Для изображения множества может подойти любая замкнутая фигура.

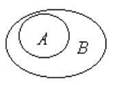
Рис. 2

Если множества заданы с помощью перечисления элементов, то отношение включения (или невключения) одного множества в другое множество можно легко установить, если сравнить элементы этих множеств. Например, если заданы множества

P ={a, b, c, d, e}; Q ={b, d, a}; R ={a, c, f},

то можно легко установить, что QÌP, но в то же время отношение RÌP для этих множеств неверно, так как элемент f из множества R не является элементом множества P.

Порядок перечисления элементов для множеств несущественен. Например, множества {b,d,a}; {a, b, d}; {d, a, b} – это по сути одно и то же множество. Если же порядок перечисления множеств является существенным, то в этом случае имеем дело не с множествами, а с последовательностями или с упорядоченными множествами (некоторые сведения о них приведены ниже). Математические свойства последовательностей существенно отличаются от математических свойств множеств.

Заметим, что несходство отношений принадлежности и включения можно иллюстрировать следующим примером. Допустим, aÎP, из чего следует, что a является элементом, а P – множеством. Можно ли в этом случае записать aÍP? Оказывается, нельзя, потому что отношение включения применимо только для двух множеств. Правильной в этом случае является запись {a}Í P, в которой слева записан не элемент, а одноэлементное множество.

Рассмотрим еще одно отношение между множествами – отношение равенства. Множества равны, если у них одни и те же элементы. Для доказательства равенства двух множеств, особенно в тех случаях, когда у них большое или бесконечное число элементов, используется следующее определение.

Определение 1. Множества A и B равны, если справедливо как AÍB, так и BÍA.

Если множества связаны отношениями AÌB или AÍB, то в этом случае множество A называют подмножеством множества B. Среди всех возможных подмножеств произвольного множества A обязательно содержится также и само множество A. Другими словами, для любого множества A всегда справедливо AÍA.

В алгебре множеств особо выделяется и часто используется множество, которое называется "пустое множество" (обозначается "Æ"). Интуитивно пустое множество означает множество, не содержащее никаких элементов. Но это интуитивное определение не раскрывает полностью его сути и роли в алгебре множеств. В большей степени его суть раскрывается в следующем предложении, которое можно отнести к одной из аксиом алгебры множеств:

Пустое множество включено в любое множество.

Для пояснения смысла этого предложения рассмотрим следующий пример. Пусть A – множество крокодилов. Ясно, что это множество может иметь какие-то подмножества. Например, множество C крокодилов, живущих в зоопарках. Тогда отношение между A и C можно записать как CÌA. Рассмотрим еще одно подмножество множества A: подмножество крокодилов, говорящих на русском языке. Ясно, что это пустое множество и, тем не менее, можем его считать подмножеством множества A. В математических рассуждениях, когда нам надо доказать, что данное множество X не существует (или существует), сводим доказательство существования к доказательству отношения X=Æ (или X¹Æ). Часто такой метод позволяет намного упростить доказательство.

Если множество задано перечислением элементов, то часто интерес представляет совокупность всех подмножеств этого множества. Например, для множества A={a, b, c} такая совокупность состоит из восьми подмножеств:

Æ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}.

Само множество А является подмножеством самого себя. Известно также простое соотношение, позволяющее сразу же узнать общее число всех возможных подмножеств множества, содержащего ровно N элементов. Оказывается, что для любого N такое число равно 2^N. Например, для нашего множества A={a, b, c} число всех возможных подмножеств равно 2³.

Обычно во многих рассуждениях используется некоторый набор множеств. Такой набор называется в алгебре множеств системой множеств. В систему множеств при этом помимо пустого множества включается и универсум, т.е. множество, для которого все множества системы множеств являются подмножествами. Другими словами, системой множеств является некоторая совокупность подмножеств некоторого множества, принятого за универсум. Например, для множеств планет, комет, звезд и т.д. в качестве универсума можно принять множество астрономических объектов.

Для универсума нет общепринятых обозначений. Далее будем обозначать его символом U.

Перейдем к операциям. Начнем с операции дополнения, которая может быть определена только тогда, когда для системы множеств задан универсум.

Определение 2. Дополнением множества A называется множество 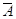, содержащее все элементы универсума, которые не являются элементами множества A.

В логике дополнению множества соответствует связка "не". Например "не красный" – любой возможный цвет кроме красного. Обычно дополнение множества обозначается с помощью черты, расположенной над символьным обозначением этого множества. Например, 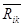 является обозначением дополнения множества .

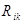Пример 1. Пусть U={a, b, c, d} и P={a, c}. Тогда $IMAGE6$={b, d}.

Определим еще две основные операции – пересечение и объединение множеств.

Определение 3. Пересечением множеств A и B называется множество C, все элементы которого являются одновременно элементами множеств A и B.

Операция пересечения множеств обозначается символом "Ç". Символически определение 3 можно записать как формулу

C = AÇB.

Например, пересечением множества всех студентов данного вуза и множества всех участников КВН, является множество студентов данного вуза, участвующих в КВН. Другой пример: пересечением множества всех чисел, делящихся на 2, и множества всех чисел, делящихся на 3, является множество