Постулаты Эйнштейна. Современный релятивистский подход к описанию природных явлений базируется на двух постулатах Эйнштейна.
Первый является естественным обобщением принципа относительности Галлилея с механических на все без исключения явления природы и может быть сформулирован как утверждение о невозможности наблюдателю, находящемуся в замкнутой системе отсчета, при помощи какого-либо физического (а значит и любого другого) опыта установить, покоится ли его система отсчета или находится в состоянии равномерного прямолинейного движения. В пользу этого постулата свидетельствует обширный житейский опыт, показывающий, что находящийся в закрытом помещении (трюме корабля) наблюдатель не в состоянии зарегистрировать факт его движения не только в результате постановки механических опытов, но и с помощью своих ощущений, в основе возникновения которых лежат, как известно, электрохимические процессы.
Вторым постулатом Эйнштейна является утверждение о постоянстве скорости света, неоднократно проверявшееся не только Майкельсоном, но и впоследствии в более точных экспериментах.
Основные выводы релятивистской кинематики. На основе сформулированных постулатов Эйнштейна пересматриваются все основные положения классической кинематики. Делается вывод о том, что понятия одновременности собитий, доительностьи временного промежутка и длины отрезка перестают носить абсолютный характер, становясь зависимыми от выбора системы отсчета, из которой ведется наблюдение (подобно тому, как при классическом описании координаты материальной точки и ее скорость носили относительный характер).
Предсказываемый релятивистской теорией эффект замедления времени состоит в том, что с точки зрения движущегося относительно рассматриваемой системы наблюдателя все интервалы времени (t’), характеризующие поцессы в этой системе (колебания маятников часов, распад нестабильных частиц, старение биологических организмов и т.д.) увеличиваются по сравнению с интервалами, наблюдаемыми в самой этой системе ( 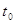 ):
):
(1) 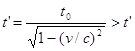 .
.
Для находящихся же в самой расматриваемой системе наблюдателей происходящие в ней процессы протекают совершенно нормально, а время у движущегося наблюдателя “течет замедленно”.
Эффект сокращения расстояний состоит в уменьшении длин отрезков с точки зрения наблюдателей, перемещающихся вдоль этих отрезков (отрезки, ориентированные перпендикулярно скорости относительного движения сохраняют свою длину неизменной):
(2) 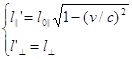
Описанные эффекты проявляются лишь при скоростях, сравнимых со скоростью света и в настоящее время экспериментально зарегистрированы в пучках ультарелятивискских частиц, создаваемых на современных ускорителях. Например, короткоживущие частицы (время жизни 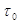 , двигаясь с околосветовыми скоростями, вопреки классическим представлениям достигают приемника, удаленного на расстояние, значительно превышающее
, двигаясь с околосветовыми скоростями, вопреки классическим представлениям достигают приемника, удаленного на расстояние, значительно превышающее 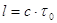 . С точки зрения неподвижного наблюдателя это явление можно объеснить эффектом замедления времени (1), “удлинняющим” жизнь частицы, с точки зрения наблюдателя, движущегося вместе с частицей - эффектом сокращения расстояния до мишени, “летящей ему навстречу” (2).
. С точки зрения неподвижного наблюдателя это явление можно объеснить эффектом замедления времени (1), “удлинняющим” жизнь частицы, с точки зрения наблюдателя, движущегося вместе с частицей - эффектом сокращения расстояния до мишени, “летящей ему навстречу” (2).
Полученные Лоренцем преобразования (10.13) являются чисто математическим следствием рассмотренных соотношений (1) и (2).
С эффектом замедления времени часто ошибочно связывают “парадокс близнецов” - утверждение о том, что двигавшийся с околосветовыми скоростями космический путешественник должен вернуться на Землю менее постаревшим, чем его брат, оставшийся дома. Кажущийся парадокс связан с тем, что всилу относительности равномерного движения с точки зрения космического путешественника эффект замедления времени должен наблюдаться на самой Земле. Реального противоречия не возникает, поскольку для того, чтобы возвратиться домой, космонавт должен в течение определенного времени двигаться с ускорением (тормозить, разворачивать корабль, вновь ускоряться), что нарушает симметрию между ним и наблюдателем на Земле (напомним, что ускорение носит абсолютный характер). Адекватное описание явлений, происходящих в ускоренно движущихся системах отсчета, выходит за рамки СТО и состаяляет предмет). Общей Теории Относительности (ОТО) .
Пространство Минковского. Широко используемая в классической физике векторная форма записи законов природы объясняется не только желанием сэкономить место, но и является математическим отражением факта инвариантности законов природы относительно поворотов выбранной системы координат в пространстве, что, разумеется, требует инвариантной формы их математической записи. Действительно, в изображенных на рис. 12_1 повернутых друг относительно друга системах координат проекции всех векторов на одноименные оси различны, но равенство
(3) $IMAGE6$
справедливо в каждой из систем, т.е. остается инвариантным относительно пространственных вращений. Помимо равенств между векторами инвариантами являются скалярные произведения векторов и вычисляемые с их помощью квадраты длин:
(4) $IMAGE7$.
Координаты же вектора в новой системе отсчета могут быть рассчитаны через координаты в старой с помощью тригонометрии:
(5) $IMAGE8$.
Последовательное релятивистское описание явлений природы должно быть инвариантным относительно переходов из одной инерциальной системы отсчета в другую, движущуюся относительно первой. Как отмечалось, при таких переходах перестает быть справедливым классический векторный закон сложения скоростей, длина векторов изменяется, а в закон преобразований их компонент (преобразования Лоренца) помимо пространственных переменных входит время:
(6) $IMAGE9$ .
В создавшейся ситуации естественным выходом был переход от несвязанных друг с другом пространственного (трехмерного) и временного (одномерного) описаний явлений к единому описанию событий в четырехмерном пространстве-времени (пространстве Минковского) при помощи четырехвекторов, три компоненты которых совпадают с обыконвенными простарнственными, а последняя дает временное описание. В этом пространстве переход в движущуюся систему отсчета рассматриваентся как обобщение понятия поворота, аналогом трехмерных траекторий являются четырехмерные кривые - мировые линии, инвариантами являются скалярные произведения четырехвекторо, определяемые соотношением:
(7) $IMAGE10$ ,
и интервалы, являющиеся аналогами длин векторов:
(8) $IMAGE11$
(следствие преобразований Лоренца).
отличающимся знаками от обычного “трехмерного” определения. В связи с этим геометрическое свойства псевдоевклидового пространства Минковского существенно отличаются от привычных свойств евклидового пространства .
Световой конус.Мировыми линиями свтовых лучей, выходящих из одной точки пространства Минковского (т.е. одновременно испущенных из одной точки трехмероного пространства) являются прямые, составляющие с осью ct одинаковый угол $IMAGE12$ и образующие световой конус (рис. 12_2).. Мировые линии всех тел могут лежать лишь внутри светового конуса, поскольку допустимые скорости движения не могут превосходить с. Лежащие в верхней части светового конуса точки пространства Минковского образуют абсолютное будущее (множество событий, на которые в принципе можно повлиять, находясь в вершине конуса), нижняя часть светового конуса соответствует абсолютному прошлому (множество событий, которые в могли повлиять на происходящее в вершине конуса). Вне светового конуса лежат абсолютно недоступные событмя (т.е. невлияющие и независимые от происходящего в вершине конуса).
Релятивистская динамика строится как обобщение классической в соответствии с требованиями релятивистской инвариантности. Важнейшую роль в ней играет четырехвектор энергии-импульса, получающийся из четырехвектора скорости домножением на инвариант массу покоя (массу тела в системе отсчета, где оно покоится):
(9) $IMAGE13$
Пространственные компоненты этого четырехвектора весьма схожи с классическим импульсом mV. Учитывая эту аналогию иногда вводят понятие релятивистской массы, величина которой возрастает с увеличением скорости движения тела относительно неблюдателя:
(10) $IMAGE14$.
С учетом (10) релятивистское уравнение движения в привычных трехмерных обозначениях принимает вид, аналогичный второму закону Ньютона в импульсной формулировке:
(11) $IMAGE15$
Возрастание релятивистской массы является одним из оснований утверждения о невозможность разогнать тело с ненулевой массой покоя до скорости света: по мере увеличения его скорости под действием постоянной силы ускорение начнет уменьшаться и стремиться к нулю при $IMAGE16$.
Эффект возрастания релятивистской массы при приближении скорости к предельной наблюдается экспериментально в ускорителях ультарелятивистских частиц сиххрофазотронов, принцип действия которых аналогичен циклотронным ускорителям. Основное отличие состоит в том, что при больших скоростях разгоняемых частиц радиусы их орбит
(12) $IMAGE17$
и периоды вращения
(13) $IMAGE18$
начинают существенно превосходить результаты расчетов по классическим формулам. Т.о. в настоящее время результаты СТО используются не только в науке, но и в инженерных расчетах.
Смысл четвертой компоненты четырехвектора энергии-импульса можно установить на основе сравнения ее произведения на скорость света с классическим выражением для кинетической энергии:
(12) $IMAGE19$
Принцип соответствия позволяет предположить, что величина
(13) $IMAGE20$
представляет собой релятивистское выражение для энергии тела, связанной с его движением. Однико, даже в случае нулевой скорости, согласно (13) лубое толо обладает энергией покоя, пропорциональной его массе. Эта колоссальная (по сравненью с характерными для классической теории масштабами) энергия до создания теории относительности оставалось “незамеченной” из-за того, что в подавляющем большинстве процессов суммарная масса составляющих систему объектов остается практически неизменной. Открытие энергии покоя имело громадное значение для развития энергетики и военной техники.
Релятивистская электродинамика. Создание релятивистской теории позволило переписать систему уравнений Максвелла в весьма элегантной и краткой четырехмерной форме:
(14) $IMAGE21$,
где
(15) $IMAGE22$
- релятивистски инвариантный четырехмерный аналог оператора Лапласа - оператор Д’Аламбера,
(16) $IMAGE23$-
-четырехмерный потенциал, состоящий из трех компонент векторного потенциала магнитного поля и скалярного потенциала электрического, $IMAGE24$ - четырехвектор плотности тока, получающийся домножением четырехвектора скорости на релятивистски-инвариантную величину электрического заряда.
Излучение электромагнитных волн. Решением Уравнения (14) в пустом пространстве являются электромагнитные волны, распространяющиеся в пустом пространстве с инвариантной относительно преобразований Лоренца скоростью с. Рассмотрение уравнения (14) с учетом зарядо и токов приводит к выводу, что электромагнитные волны создаются электрическими зарядами при их ускоренном движении. При этом электромагнитное поле, создаваемое точечным зарядом на больших расстояниях от него (рис. 12_3) имеет вид
(17) $IMAGE25$,
т.е. убывает гораздо медленнее, чем статические поля. Это свойство обуславливает удобство использования переменных электромагнитных полей в целях связи.
Происхождение силы Лоренца. Существование зависящей (вопреки требованием классической теории) от скорости относительно наблюдателя магнитной силы Лоренца в релятивистской теории находит весьма “неожиданное” объяснение. Сами магнитные взаимодействия и описывающая их сила являются “лишними” в теории электричества, т.е. адекватное описание реальности возможно и бех их использования на основе закона Кулона и релятивистских формул преобразования физических величин при переходах из одной системы отсчета в другую. Релятивистских эффект изменения силы взаимодействия между двумя зарядами с точки зрения движущегося наблюдателя был замечен экспериментально задолго до создания теории относительности и отнесен за счет существования “новой” магнитной силы, которую пришлось наделить весьма странными свойствами. Если бы теория магнетизма создавалась в наши дни, “магнитные взаимодейстивя” были бы предсказаны теоретически как релятивистская поправка к электростатическим.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://study.online.ks.ua/