Федеральное агентство по образованию Российской Федерации
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО
Кафедра компьютерной алгебры и теории чисел
Основная теорема алгебры
Курсовая работа
студента 1 курса 121 группы механико-математического факультета
Батура Ирина Сергеевна
Научный руководитель Е.В. КОРОБЧЕНКО, ассистент
Зав. кафедрой В.Н.КУЗНЕЦОВ, д.т.н., профессор
САРАТОВ
2009 год
СОДЕРЖАНИЕ
1. Введение
2. Основные определения, используемые в курсовой работе
3. Элементы теории пределов для комплексных чисел
4. Доказательство основной теоремы
5. Список используемой литературы
1. ВВЕДЕНИЕ
Данная работа посвящена Основной теореме Алгебры, изучению существования корней в поле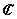 
. Как предположение эта теорема впервые встречается у немецкого математика Питера Роуте(1617г.). Д’Аламбер первым в 1746г. опубликовал доказательство этой теоремы. Его доказательство основывалось на лемме. Доказательство это было бы совершенно строгим, если бы Д’Аламбер мог доказать, что-то на комплексной плоскости значение модуля многочлена достигает наименьшего значения. Во второй половине 18 века появляются доказательства Эйлера, Лапласа, Лагранжа и других. Во всех этих доказательствах предполагается заранее, что какие-то "идеальные" корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. Со времен доказательства теоремы в алгебре было открыто очень много нового, поэтому сегодня "основной" эту теорему назвать уже нельзя: это название теперь является историческим.
Целью моей работы является выявления, что поле 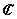комплексных чисел алгебраически замкнуто. Для доказательства Основной теоремы Алгебры я использовала ряд лемм: лемма Даламбера и лемма о достижении точной нижней грани значений.
При написании работы мною была использована следующая литература: Д.К.Фадеев "Лекции по алгебре", Л.Д.Кудрявцев "Курс математического анализа". А.Г.Курош "Курс высшей алгебры".
2. Основные определения, используемые в курсовой работе
Множества, удовлетворяющие требованиям:1-операция сложения,2-операция умножения,3-связь операций сложения и умножения, и содержащие хотя бы один элемент, отличный от нуля, называется полями.
Множество комплексных чисел 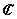можно определить как множество упорядоченных пар 
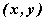действительных чисел, 
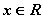, $IMAGE6$, в котором введены операции сложения и умножения согласно следующему определению:
$IMAGE7$ $IMAGE8$
В результате этого определения множество указанных пар превращается в поле, т.е. удовлетворяет условиям 1,2,3. Полученное таким образом поле, называется полем комплексных чисел.
Последовательность комплексных чисел - это функция, определенная на множестве натуральных чисел и имеющая своими значениями комплексные числа.
Последовательность $IMAGE9$ называется подпоследовательностью $IMAGE10$, если для любого k существует такое натуральное $IMAGE11$, что $IMAGE12$= $IMAGE13$, причем $IMAGE14$Б $IMAGE15$ тогда и только тогда, когда $IMAGE16$.
Комплексное число – расширение множества вещественных чисел, обычно обозначается 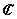. Любое комплексное число может быть представлено как формальная сумма $IMAGE18$, где x и y— вещественные числа, i— мнимая единица, то есть число, удовлетворяющее уравнению $IMAGE19$.
Вещественное число (действительное число) – любое положительное число, отрицательное число или нуль.
Функция – 1) Зависимая переменная величина; 2) Соответствие $IMAGE20$ между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение величины y (зависимой переменной или функции в значении 1).
Теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.
Последовательность называется ограниченной на множестве Е, если существует такая постоянная М>0, что для всех $IMAGE21$ и всех $IMAGE22$ выполняется неравенства $IMAGE23$
Последовательность сходится к функции f равномерно на множестве Е, если для любого $IMAGE24$ существует такой номер $IMAGE25$, что если $IMAGE26$, то для всех $IMAGE21$выполняется неравенство $IMAGE28$. Последовательность называется равномерно сходящейся на множестве Е, если существует функция f, к которой она равномерно сходится на Е.
3. Элементы теории пределов для комплексных чисел
В моей работе полиномы рассматриваются только над полями 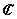и $IMAGE30$ как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля 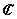) носит название основной теоремы алгебры. $IMAGE32$
Определение: Пусть задана последовательность комплексных чисел $IMAGE33$ . Число $IMAGE34$ называется ее пределом, если для любого действительного числа $IMAGE24$ существует такой номер $IMAGE25$, что при $IMAGE26$ выполняется неравенство $IMAGE38$. В этом случае пишут lim $IMAGE39$, а=lim $IMAGE40$, b=lim $IMAGE41$. Предельное соотношение lim $IMAGE42$=c равносильно соотношению $IMAGE43$, ибо
max $IMAGE44$ $IMAGE45$ $IMAGE46$ $IMAGE45$ $IMAGE48$ $IMAGE49$
Последовательность $IMAGE42$такая, что $IMAGE51$ $IMAGE45$ R, при некотором R, называется ограниченной.
Для вещественных переменных известная теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. То же самое верно и для последовательностей, составленных из комплексных чисел.
Действительно, пусть $IMAGE53$ограниченная последовательность, т.е. $IMAGE54$, тогда $IMAGE55$, так что $IMAGE40$ есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность $IMAGE57$. Рассмотрим соответствующую подпоследовательность мнимых частей $IMAGE58$. Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность $IMAGE59$.
Соответствующая подпоследовательность комплексных чисел имеет сходящиеся последовательности вещественных и мнимых частей и, следовательно, сходятся, и ее предел равен $IMAGE60$.
4. Доказательство основной теоремы
Прежде чем приступить к формальному доказательству, наметим его идею. Пусть $IMAGE61$-полином, рассматриваемый как функция от комплексной переменной $IMAGE62$.Представим себе "график" функции $IMAGE63$, считая , что значения $IMAGE62$ изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения $IMAGE65$ откладываются вверх в направлении оси $IMAGE66$. Мы установим, что $IMAGE67$ являются непрерывными функциями от $IMAGE62$ на всей плоскости комплексной переменной. Функция $IMAGE69$от комплексной переменной $IMAGE62$ называется непрерывной в точке $IMAGE71$, если достаточно близким к $IMAGE71$ значениями $IMAGE62$ соответствует сколь угодно близкие к $IMAGE74$значения $IMAGE69$.В более точных терминах - для любого $IMAGE24$найдется такое $IMAGE77$, что $IMAGE78$, как только $IMAGE79$.
Непрерывность $IMAGE65$ дает основания представлять себе график $IMAGE63$ в виде непрерывной поверхности, накрывающей плоскость $IMAGE82$, и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение $IMAGE71$ , в котором $IMAGE84$, и, тем самым, $IMAGE85$, т.е. что поверхность $IMAGE63$ доходит до плоскости $IMAGE82$в точке $IMAGE71$. Мы докажем, что если дана точка на поверхности $IMAGE63$,которая расположена выше плоскости $IMAGE82$, то в ее окрестности найдется точка поверхности расположенная ниже данной точки. Тогда останется только доказать, что на поверхности $IMAGE63$ существует самая низкая точка, скажем, при $IMAGE92$ . Она не может находиться выше плоскости $IMAGE82$, ибо тогда она была бы самой низкой точкой. Следовательно, $IMAGE85$ и , следовательно $IMAGE84$, т.е. $IMAGE71$ корень полинома $IMAGE61$.
Теперь приступим к доказательству основной теоремы, разбив это доказательство на цепочку лемм.
Лемма 1. Дан полином $IMAGE98$ c нулевым свободным членом.
Тогда для любого $IMAGE24$найдется такое $IMAGE77$, что $IMAGE101$, как только $IMAGE102$.
Доказательство: Пусть $IMAGE103$. Тогда
$IMAGE104$
Положим
$IMAGE105$Если $IMAGE106$
то $IMAGE107$
что и требовалось доказать.
Лемма 2. Полином есть непрерывная функция во всех точках плоскости комплексной переменной.
Доказательство: Пусть дан полином $IMAGE61$и точка $IMAGE71$. Расположим полином по степеням
$IMAGE110$,
Тогда $IMAGE111$так что
$IMAGE112$
Правая часть есть полином от $IMAGE113$ с нулевым свободным членом.
По лемме 1 для любого $IMAGE24$ найдется такое $IMAGE77$, что $IMAGE116$как только $IMAGE117$ что и требовалось доказать.
Лемма 3. Модуль полинома есть непрерывная функция.
Доказательство: Из неравенства $IMAGE118$ следует, что для данного $IMAGE24$ то $IMAGE120$, которое "обслуживает" $IMAGE61$, подходит и для $IMAGE65$. Действительно, при $IMAGE117$ имеем
$IMAGE124$
Лемма 4. (о возрастании модуля полинома). Если $IMAGE61$-полином, отличный от константы, то для любого М>0 существует такое R>0, что $IMAGE126$M,как только $IMAGE127$.
Это означает, что любая горизонтальная плоскость $IMAGE128$отрезает от поверхности $IMAGE63$ конечный кусок, накрывающий часть круга |z|≤R.
Доказательство: Пусть
$IMAGE130$
где $IMAGE131$полином от $IMAGE132$c нулевым свободным членом.
В силу леммы 1 для $IMAGE133$ найдется такое $IMAGE77$, что при $IMAGE135$, будет $IMAGE136$. Модуль $IMAGE137$ может быть сделан сколь угодно большим, именно, при $IMAGE138$ будет $IMAGE139$. Возьмем $IMAGE140$ $IMAGE141$ Тогда при $IMAGE127$ будет
$IMAGE135$ и $IMAGE144$ так что $IMAGE145$
Лемма 5. Точная нижняя грань значений $IMAGE65$ достигается, т.е. существует такое $IMAGE71$, что $IMAGE148$ при всех $IMAGE62$.
Доказательство: Обозначим точную нижнюю грань $IMAGE61$ через $IMAGE151$. Возьмем последовательностью $IMAGE32$ $IMAGE153$ стремящихся к $IMAGE151$сверху. Каждая из этих чисел не является нижней гранью значений $IMAGE65$, ибо $IMAGE151$-точная нижняя грань. Поэтому найдутся $IMAGE157$ такие, что $IMAGE158$ . Воспользуемся теперь леммой о возрастании модуля. Для $IMAGE159$ найдем такое $IMAGE160$, что при $IMAGE127$ будет $IMAGE162$ Отсюда следует, что $IMAGE163$ при все $IMAGE164$. Последовательностью $IMAGE157$ оказалась ограниченной, и из нее можно извлечь сходящуюся подпоследовательность $IMAGE166$ . Пусть ее предел равен $IMAGE71$ . Тогда $IMAGE168$ в силу непрерывности $IMAGE65$. Кроме того, $IMAGE170$. Поэтому $IMAGE171$ Итак $IMAGE172$, что и требовалось доказать.
Лемма 6. (Лемма Даламбера). Пусть $IMAGE61$ полином отличный от константы, и пусть $IMAGE174$. Тогда найдется такая точка $IMAGE175$, что
$IMAGE176$
Геометрический смысл этой леммы: если на поверхности $IMAGE63$ дана точка, находящаяся выше плоскости $IMAGE82$, то на ней найдется другая точка, расположенная ниже первой.
Доказательство: Расположим полином $IMAGE61$ по степеням
$IMAGE180$
Тогда $IMAGE181$ Идея доказательства состоит в том, чтобы за счет первого отличного от нуля слагаемого "откусить кусочек" от $IMAGE182$, а влияние дальнейших слагаемых сделать незначительным. Пусть $IMAGE183$ – первое отличное от нуля слагаемое после $IMAGE182$, так что $IMAGE185$ (если k>1). Такое слагаемое имеется, так как $IMAGE61$ не константа. Тогда
$IMAGE187$ $IMAGE188$+
+ $IMAGE188$( $IMAGE190$+…+ $IMAGE191$))=
= c0 (1+ $IMAGE188$+ $IMAGE193$ $IMAGE194$).
Здесь
$IMAGE194$= $IMAGE32$ $IMAGE197$
есть полином от $IMAGE198$ с нулевым свободным членом. По лемме 1 для $IMAGE199$= $IMAGE200$ найдется такое $IMAGE120$,что | $IMAGE194$|< $IMAGE200$, как только | $IMAGE198$|< $IMAGE120$. Положим $IMAGE206$ = $IMAGE160$( $IMAGE208$) и $IMAGE209$ $IMAGE210$. Тогда
$IMAGE211$.
Выберем $IMAGE212$ так, что $IMAGE213$. Для этого нужно взять $IMAGE214$. Далее, положим $IMAGE215$, т.е. возьмем $IMAGE216$. При таком выборе будет $IMAGE217$. Теперь положим
$IMAGE218$ при $IMAGE219$ и $IMAGE216$. Тогда $IMAGE221$ и
| $IMAGE222$|= $IMAGE223$ $IMAGE224$.
Лемма доказана.
Заметим, что с тем же успехом мы могли бы взять $IMAGE225$ при $IMAGE226$ так что при k>1 (т.е. в случае, когда $IMAGE227$-корень кратности $IMAGE228$ полинома $IMAGE229$)имеется k направлений спуска по поверхности $IMAGE230$ $IMAGE231$. Они разделяются $IMAGE164$ направлениями подъема при $IMAGE233$
Действительно, в этих направлениях
$IMAGE234$ и $IMAGE235$
Так что если $IMAGE227$ есть корень производной кратности $IMAGE228$, то поверхность $IMAGE63$ в окрестности точки $IMAGE227$ "гофрирована" так, что на ней имеется $IMAGE164$ "долин&q