База рефератов

Академия труда и социальных отношений

Курганский филиал

Социально-экономический факультет

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: «Общий курс высшей математики»

Студент гр. ЗМб 1338

Ст. преподаватель

Курган – 2009

Задание 03

В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба, если А(4,2), С(16;18), 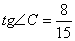. Сделать чертеж.

Решение:

Зная координаты вершин А и С запишем уравнение диагонали АС как уравнение прямой, проходящей через две заданные точки:

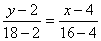
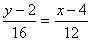
12(y-2)=16(x-4);

12y-24=16х-64

16х-12у-40=0 /:4

4х-3у-10=0 – уравнение диагонали А С в форме общего уравнения прямой.

Перепишем это уравнение в форме уравнения прямой с угловым коэффициентом:

-3y=-10-4х;

3y=4x-10;

y= 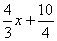 откуда k А С=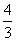

Так как в ромбе диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен

К_ВD = $IMAGE6$ $IMAGE7$

Само же уравнение диагонали BD найдем как уравнение прямой, проходящей через заданную точку в направлении, определяемом угловым коэффициентом К_BD.

В качестве «заданной точки» возьмем точку Е пересечения диагоналей ромба, которая лежит на середине отрезка АС, вследствие чего:

$IMAGE8$

$IMAGE9$

Е (10;10)

Итак, уравнение диагонали BD запишем в виде

у – yE= К_ВD (x-xE)

y-10= $IMAGE7$ (x-10);

y-10= $IMAGE7$x+ $IMAGE12$ / $IMAGE13$ 4

4у-40=-3х+30

3х+4у-70=0 – уравнение диагонали BD

Чтобы найти уравнение сторон ромба, надо определить только угловые коэффициенты К_АВ = К_CD и К_ВС = К_AD прямых, на которых эти стороны лежат, ибо точки, через которые эти прямые проходят, известны – это вершины А и С ромба.

Для определения указанных угловых коэффициентов воспользуемся формулой $IMAGE14$, позволяющей вычислять тангенс угла φ между двумя заданными прямыми по их угловым коэффициентам К₁ и К₂; при этом угол φ отсчитывается против часовой стрелки от прямой у = К₁х + b₁ до прямой у = К₂х + b₂. Формула оказывается удобной, потому что уравнение диагонали АС уже найдено (и, следовательно, известен ее угловой коэффициент К_АС), а положение сторон ромба относительно этой диагонали однозначно определяется внутренними углами А и С, которые равны между собой и для которых по условию известен их тангенс ( $IMAGE15$).

Так диагонали ромба делят его углы пополам, то, положив $IMAGE16$ из формулы $IMAGE17$       для тангенса двойного угла при $IMAGE18$ найдем tg φ:

$IMAGE19$

Положим z = tg φ; тогда $IMAGE20$, тогда

15 $IMAGE13$ 2z = 8 (1-z²)

30z=8-8z²

8z²+30z-8=0 /:2

4z²+15z-4=0

D=15²-4 $IMAGE13$ 4 $IMAGE13$ (-4)= 225+64=289

z₁= $IMAGE24$ $IMAGE25$;

z₂₌ $IMAGE26$ $IMAGE27$

Но т.к. угол в ромбе φ всегда острый корень z₂=-4 отбрасываем и получаем в итоге, что tg φ = $IMAGE28$

Угол φ является углом между прямыми ВС и АС, с одной стороны, и прямыми АС и CD – с другой (см. чертеж).

Потому в первом случае по формуле $IMAGE14$ имеем $IMAGE30$

откуда при $IMAGE31$ то получим

$IMAGE32$

4( $IMAGE33$)=1+ $IMAGE34$;

$IMAGE35$= $IMAGE36$ / $IMAGE13$3

16-12 K_BC=3+4K_BC;

16 K_BC=13;

K_BC= $IMAGE38$

Во втором случае по формуле $IMAGE14$ имеем $IMAGE38$= $IMAGE41$;

При К_АС = 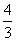 получим:

$IMAGE43$;

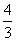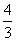4(KcD- )=1+ KcD;

4KcD- $IMAGE46$=1+ $IMAGE47$ KcD / $IMAGE13$3;

12KcD-16=3+4KcD;

8KcD =19

KcD= $IMAGE49$

Так как противоположные стороны ромба параллельны, то тем самым мы определили угловые коэффициенты всех его сторон.

К_CD = K_AB = $IMAGE49$ ;

K_BC = K_AD = $IMAGE38$.

Зная теперь эти угловые коэффициенты и координаты вершин А и С, по уже использовавшимся выше формулам найдем уравнения прямых АВ, CD, BC и AD.

Уравнение АВ: у – уA = K_{A B} (х – хA),

у -2 = $IMAGE49$ (х-4) / $IMAGE13$8;

8у-16=19х-76;

19 х-8 у-60=0.

Уравнение CD: у – у_C= К_CD(х – x_C)

у -18= $IMAGE49$( х-16) / $IMAGE13$8;

8у -144=19х-304;

19 х-8 у-160=0.

Уравнение ВС: у – у_C= К_BC ( х x_C);

у -18= $IMAGE38$( х - 16);

у - 18= $IMAGE38$ х – 13 / $IMAGE13$16;

16у -288 = 13х - 208;

13х -16 у +80=0

Уравнение AD: у – уA = КA_D( х -xA);

у -2= $IMAGE38$( х -4);

у -2= $IMAGE38$ х - $IMAGE61$ / $IMAGE13$16;

16у -32= 13х-52;

13х-16у-20=0

Вершины ромба являются точками пересечения его соответствующих сторон. Поэтому их координаты найдем путем совместного решения уравнений этих сторон.

$IMAGE63$

19х -8у -60 = 0    / $IMAGE13$ (-2)

13х -16у +80= 0

$IMAGE65$-38х+16у+120=0

13х-16у+80=0

-25х = - 200

х = 8

13 $IMAGE13$ 8 -16у+80=0

104-16у+80=0

16у=184

у=11,5 т.В (8;11,5)

Для вершины D:

$IMAGE67$19х -8у +-160 = 0                  / $IMAGE13$ (-2)

$IMAGE69$13x - 16 y – 20 = 0

-38х + 16у +320 = 0

13x - 16 y – 20 = 0

-25х = - 300

х=12

13 $IMAGE13$ 12 - 16у-20 = 0

156 -16 у-20=0

16у – 136

у=8,5 т.D (12;8,5)

Координаты этих точек удовлетворяют ранее найденному уравнению 3х + 4у - 70 = 0 диагонали BD, что подтверждает их правильность.

Площадь ромба вычислим по формуле S = ½ d₁d₂, где d₁ и d₂ – диагонали ромба.

Полагая d₁ = |АС|, а d₂ = |BD|, длины этих диагоналей найдем как расстояния между соответствующими противоположными вершинами ромба:

d₁ = $IMAGE71$

d₂ = $IMAGE72$

В итоге площадь ромба будет равна S = $IMAGE73$ ∙ 20 ∙ 5 = 50 кв.ед.

Ответ:

АС: 4х - 3у - 10 = 0;

BD: 3х + 4у - 70= 0;

АВ: 19х -8у -60 = 0;

CD:19 х -8у - 160 = 0;

ВС: 13х -16у + 80 = 0;

AD: 13х -16у – 20=0;

В (8;11,5);

D (12; 8,5);

S = 50 кв.ед.

Задание 27

Найти предел

а) $IMAGE74$

Решение:

а) Функция, предел которой при х→ 2 требуется найти, представляет собой частное двух функций. Однако применить теорему о пределе частного в данном случае нельзя, так как предел функции, стоящей в знаменателе, при х→ 2 равен нулю.

Преобразуем данную функцию, умножив числитель и знаменатель дроби, находящейся под знаком предела, на выражение $IMAGE75$, сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:

$IMAGE74$= $IMAGE77$= $IMAGE78$=

$IMAGE79$= $IMAGE80$=

$IMAGE81$

2 х ² - 3 х - 2=0

D=3 ² -4 $IMAGE13$2 $IMAGE13$(-2)=9+16=25

х1 = $IMAGE84$= $IMAGE85$=2;

х2 = $IMAGE86$= $IMAGE87$= - $IMAGE88$

$IMAGE89$= $IMAGE90$=

$IMAGE91$= $IMAGE92$= $IMAGE93$=12,5

Ответ: 12,5

б) $IMAGE94$

Умножим числитель и знаменатель дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:

$IMAGE94$= $IMAGE96$=

$IMAGE97$=

$IMAGE98$= $IMAGE99$=

$IMAGE100$ $IMAGE101$ $IMAGE102$+ $IMAGE103$=

$IMAGE104$ $IMAGE105$ $IMAGE106$ $IMAGE107$

Найдем каждый сомножитель.

$IMAGE108$= $IMAGE109$= $IMAGE110$= $IMAGE111$= $IMAGE112$

$IMAGE113$ $IMAGE114$+ $IMAGE115$)=( $IMAGE116$=1+1=2.

$IMAGE117$ $IMAGE118$

Предел $IMAGE119$ есть первый замечательный предел.

Таким образом.

$IMAGE120$ после замены t=3x будет равен $IMAGE121$=3

Аналогично $IMAGE122$=5

Получим

$IMAGE123$= $IMAGE124$

$IMAGE125$ $IMAGE126$1

В итоге получим: $IMAGE127$

Ответ: $IMAGE128$

в) $IMAGE129$

Преобразуем основание данной функции:

$IMAGE130$ $IMAGE131$ $IMAGE132$ $IMAGE133$

Ведем новую переменную t= $IMAGE134$, тогда $IMAGE135$ $IMAGE136$

t (4x-1) = 2

4xt – t = 2

4xt =2 + t

x= $IMAGE137$

x= $IMAGE138$

Заметим, что предел функции t при x → ∞ равен нулю т.е t → 0 при x → ∞. Следовательно

$IMAGE129$= $IMAGE140$= $IMAGE141$=

= $IMAGE142$

Воспользуемся теоремой о пределе произведения, следствием теоремы о пределе сложной функции, вторым замечательным пределом получим.

$IMAGE143$

Ответ: $IMAGE144$

г) $IMAGE145$

Представим выражение под знаком предела в виде

$IMAGE145$= $IMAGE147$= $IMAGE148$=

$IMAGE149$ $IMAGE150$= $IMAGE150$ $IMAGE152$=

$IMAGE153$ $IMAGE154$

Найдем значение каждого предела:

$IMAGE150$= $IMAGE156$=1

$IMAGE157$= - ln e следствие из второго замечательного предела.

$IMAGE158$=3 $IMAGE159$ $IMAGE160$=3 $IMAGE13$1=3

В итоге получим

$IMAGE162$=1 $IMAGE163$= $IMAGE164$= $IMAGE165$

Ответ: $IMAGE166$

Задание 50

Найти производную функции

а) $IMAGE167$

Решение:

при решении будем применять правила дифференцирования частного произведения и сложной функции.

$IMAGE168$=

$IMAGE169$

$IMAGE170$= $IMAGE171$=

$IMAGE172$=

$IMAGE173$ $IMAGE174$

б) $IMAGE175$

$IMAGE176$ $IMAGE177$ $IMAGE178$+ $IMAGE179$

$IMAGE180$+ $IMAGE181$= $IMAGE182$+ $IMAGE181$=

= $IMAGE184$+ $IMAGE181$= $IMAGE186$+ $IMAGE187$

$IMAGE188$

в) $IMAGE189$

Решение:

$IMAGE190$

$IMAGE191$

$IMAGE192$

$IMAGE193$

$IMAGE194$

$IMAGE195$

$IMAGE196$

$IMAGE197$

г) $IMAGE198$

$IMAGE199$= $IMAGE200$=

$IMAGE201$= $IMAGE202$ $IMAGE203$-

$IMAGE204$= $IMAGE205$- $IMAGE206$= $IMAGE207$-

- $IMAGE208$= $IMAGE207$-

$IMAGE210$= $IMAGE211$=

$IMAGE212$

Задание 73

Вычислить приближенное значение функции f (x) = ln $IMAGE213$ в точке x1 заменив приращение функции в точке х₀ = 0 ее дифференциалом. Если известно a=8; b=13; c=21;x1=0.013

Решение:

Если приращение аргумента ∆х = х₁ – х₀ достаточно мало по абсолютной величине, то приращение функции ∆f = f (x₁) – f (x₀) приближенно равно дифференциалу функции df. Поэтому справедлива формула

f (x₀ + _∆x) ≈ f (x₀) + f ^/ (x₀) _∆x.

Для вычисления приближенного значения функции у = ln $IMAGE214$ в точке х₁ = 0,013 вычислим производную этой функции в точке х₀ = 0:

f ^/ (x) = $IMAGE215$= $IMAGE216$   $IMAGE217$=

$IMAGE218$= $IMAGE219$= $IMAGE220$

f ^/ (x) = f ^/ (0) = $IMAGE221$= $IMAGE222$=-1

Подставив в формулу получим; f (0,013) $IMAGE223$=-0,013

Ответ: -0,013

Задание 96

Исследовать функцию $IMAGE224$ и построить ее график.

Решение

1. Область определения данной функции – вся числовая ось, то есть интервал (-∞; +∞), так как выражение

f (x) = $IMAGE225$

в правой части аналитического задания функции имеет смысл при любом действительном х.

2. Как элементарная функция, данная функция является непрерывной в каждой точке своей области определения, то есть в каждой точке числовой оси.

3. Найдем все асимптоты графика данной функции.

Вертикальных асимптот график данной функции у = f (x) не имеет, поскольку последняя непрерывна на всей числовой оси формула

Для отыскания наклонной асимптоты при х→ +∞ вычислим следующие два предела k = lim y/x и b = lim (y – kx)

Если оба они существуют и конечны, то прямая у = kx + b является наклонной асимптотой при х→+∞ графика функции у = f (x)

Прежде чем обращаться к вычислению указанных пределов, напомним тождество √х² = |х| (1), из которого следует, что при x > 0 √х² = х ,

а при х < 0 √х² = -х или х = -√х² (2)

Приступая к вычислению первого предела, разделим числитель и знаменате