Автор: Фильчев Э.Г.
Решение кубического уравнения в системе mn параметров
Решение кубического уравнения на основе современных методов не представляется тривиальным. В любом справочнике по математике предлагаются следующие методы
- разложение левой части на линейные множители ( если возможно )
- с помощью формулы Кардана
- применение специальных таблиц
(см. например, И.Н.Бронштейн. К.А.Семендяев. Справочник по математике …М. Наука 1980. стр.219).
В данной статье рассматривается метод решения любых кубических уравнений включая неприводимый случай формулы Кардана!
Задача "Задано кубическое уравнение вида ax3 + bx2+ cx + d = 0.
Используя формулы системы mn параметров предложить метод определения нулей исходного уравнения ". Пусть а = 1.
Решение
На сайте fgg-fil1.narod.ru/fmat16.doc приведена, полученная автором, формула mn преобразования степенной функции. Для кубического уравнения эта формула имеет вид
(2mn)2 + ( 3x + b )(2mn) + 3x2 + 2bx +с = 0 ( 1 )
где
x - любой из нулей ( корней) исходного уравнения
2mn - разность любой пары из трех нулей исходного уравнения
Решив уравнение (1) относительно х и подставив это значение в исходное уравнение, в результате, после простых, но громоздких преобразований, получим
(2mn)6 +2( 3c – b2 )(2mn)4+(3c – b2 )2(2mn)2 + [ 4( 3c – b2 )3 + ( 2b3 – 9bc + 27d )2]/27 = 0 ( 2 )
Это уравнение устанавливает связь коэффициентов исходного уравнения с параметром (2mn) и является кубическим относительно (2mn)2. На основании формул Виета и уравнения (2) можно сделать следующее утверждение
Утверждение1 "Для любого кубического уравнения вида x3 + bx2+ cx + d = 0 справедливы уравнения
3x2 + 2bx + c = - (2mn)1( 2mn)2
2(3c-b2) = - [(2mn)12+( 2mn)22+( 2mn)32 ]
[4(3c-b2)3+(2b3 - 9bc+27d)2]/27 = - (2mn)12( 2mn)22( 2mn)32
где (2mn)j - разность любой пары корней исходного уравнения.
x - один ( любой ) из корней исходного уравнения. "
1. Для любого кубического уравнения вида x3 + bx2+ cx + d = 0 определяем значение
D1 = -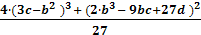 
= - (2mn)12 ∙ ( 2mn)22 ∙ ( 2mn)32
2. Определяем значение
D2 = - 2( 3c – b2 ) = - [(2mn)12 + ( 2mn)22 + ( 2mn)32]
Из этих уравнений следует, что
- если выражение - 2(3c - ) - целое число, то оно разложимо на сумму трех квадратов
- и если при этом выполняется равенство D1 = - (2mn)12( 2mn)22( 2mn)32 , то в результате получим решение для (2mn)1,( 2mn)2,( 2mn)3.
3. Определяем значение корней исходного уравнения
3x2 + 2bx + c = - (2mn)1( 2mn)2
3x2 + 2bx + c = (2mn)1( 2mn)2
3x2 + 2bx + c = - (2mn)1( 2mn)3
3x2 + 2bx + c = (2mn)1( 2mn)3
3x2 + 2bx + c = - (2mn)2( 2mn)3
3x2 + 2bx + c = (2mn)2( 2mn)3
Задача решена !
Пример 1 Решить уравнение с помощью формул системы mn параметров
x3 - 9x2+ 23x - 15 = 0
где a =1, b = - 9, c = 23, d = -15
Решение
1. Определяем значение D1 = = -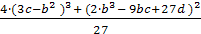 
-→ D1 = - [4(69-81)3+( - 1458 + 1863 - 405)2]/27= - [4(69-81)3+0]/27= 256 = 162
Обратим внимание, что в этом примере (2b3-9bc+27d) = 0
2. Определяем значение D2 = - 2(3c - )
-→ D2 = - 2( 3∙23 - 81 ) = 24 = 4 + 16 + 4
Это единственное разложение числа 24 на три квадрата. Следовательно
имеем (2mn)1 = 2, (2mn)2 = 4, (2mn)3 = 2.
3. Определяем значение нулей ( корней ) исходного уравнения
3.1 3x2 + 2bx + c = - (2mn)1( 2mn)2
-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 31 = 0. Нет действительных решений.
3.2 3x2 + 2bx + c = (2mn)1( 2mn)2
-→ 3x2 - 18x + 23 = -> 3x2 - 18x + 15 = 0 -→ x2 - 6x + 5 = 0
-→ X1 = 3 + 2 = 5 , X2 = 3 - 2 = 1
Здесь X1 = 5 - одно из решений исходного уравнения.
Здесь X2 = 1 второе решение исходного уравнения.
3.3 3x2 + 2bx + c = - (2mn)1( 2mn)3
-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 27 = 0 -→ x2 - 6x + 9 = 0
-→ X2 = 3
Здесь X = 3 - последнее из решений исходного уравнения.
3.4 3x2 + 2bx + c = (2mn)1( 2mn)3
-→ 3x2 - 18x + 23 = 2∙2 -→ 3x2 - 18x + 19 = 0. Нет решений исходного уравнения.
Задача решена!
Пример 2 Решить уравнение с помощью формул системы mn параметров
x3 - 20x2+ 113x - 154 = 0
где a =1, b = - 20, c =113, d = -154
Решение
1. Определяем значение D1 = -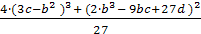
-→D1 = - [4(339-400)3+( - 16000 + 20340 - 4158)2]/27= - [- 907924+33124]/27=32400
2. Определяем значение D2 = - 2(3c - )
-→ D2 = - 2( - 400 ) = 122 = 32 + 72 + 82 = 42 + 52 + 92
Здесь имеет место два представления числа 122 в виде суммы трех квадратов.
Поэтому, проверяем на соответствие с числом D1 = 32400.
2.1 32 ∙ 72 ∙ 82 = 28224 ≠ 32400
2.2 42 ∙ 52 ∙ 92 = 32400 . Этот вариант подходит!
-→ (2mn)11 = 4, (2mn)12 = - 4,
(2mn)21 = 5, (2mn)22 = - 5,
(2mn)31 = 9, (2mn)32 = - 9.
3. Определяем значение нулей ( корней ) исходного уравнения
3.1 3x2 + 2bx + c = - (2mn)1( 2mn)2
-→ 3x2 - 40x + 113 = - 4∙5 -> 3x2 - 40x + 133 = 0.
-→ X1 = 7, X2 =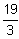 
4. Таким образом, определен один из корней исходного кубического уравнения X1 = 7, и кроме того, известны значения (2mn)11 ÷ (2mn)32. Этих данных достаточно для определения двух остальных корней.
4.1 Пусть (2mn)11 = 4 = (X1 - X2) -→ X2 = X1 – 4 = 7 – 4 = 3. Нет решения(это не корень).
4.2 Пусть (2mn)12 = - 4 = (X1 - X2) -→ X2 = X1 + 4 = 7 + 4 = 11. Это второй корень.
4.3 Пусть (2mn)21 = 5 = (X2 - X3) -→ X3 = X2 - 5 = 7 - 5 = 2. Это третий корень.
Решением исходного уравнения будет X1 = 7, X2 = 2, X3 = 11.
Расчет закончен !
Пример 3 Решить уравнение с помощью формул системы mn параметров
x3 - 10x2 - 49x + 130 = 0
где a =1, b = - 10, c = - 49, d = 130
Решение
1. Определяем значение D1 = -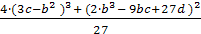
-→D1 = - [4( -147 - 100)3+( 2000 + 4410 - 3510)2]/27= - [- 60276892+8410000]/27= 1920996
2. Определяем значение D2 = - 2( 3c - )
-→ D2 = - 2( - 147 - 100 ) = 494 = 12 + 32 + 222 = 22 + 72 + 212 = 72 + 112 + 182
Из этих трех вариантов представления числа 494 в виде суммы трех квадратов подходит последний вариант , т.к. 72 ∙ 112 $IMAGE6$ 182 = 1920996
-→ (2mn)11 = 7, (2mn)12 = - 7,
(2mn)21 = 11, (2mn)22 = - 11,
(2mn)31 = 18, (2mn)32 = - 18.
3. Определяем значение нулей ( корней ) исходного уравнения
3.1 3x2 + 2bx + c = - (2mn)11( 2mn)21
-→ 3x2 - 20x - 49 = 7∙11 -> 3x2 - 20x - 126 = 0. Эти значения X не подходят!
3.2 3x2 + 2bx + c = (2mn)11( 2mn)22
-→ 3x2 - 20x - 49 =- 77 -→ 3x2 - 20x + 28 = 0.
-→ X1 = $IMAGE7$ , X2 = 2 – это один из корней исходного уравнения!
4. Таким образом, определен один из корней исходного кубического уравнения X1 = 2, и кроме того, известны значения (2mn)11 ÷ (2mn)32. Этих данных достаточно для определения двух остальных корней.
4.1 Пусть (2mn)11 = 7 = (X1 - X2) -→ X2 = X1 – 7 = 2 – 7 = - 5. Это второй корень!
4.2 Пусть (2mn)12 = - 7 = (X1 - X2) -→ X2 = X1 +7 = 2 + 7 = 9. Это не корень.
4.3 Пусть (2mn)21 = 11 = (X1 - X3) -→ X3 = X1 - 11= 2 - 11 = - 9. Это не корень.
4.4 Пусть (2mn)21 = -11 = (X1 - X3) -→ X3 = X1 + 11= 2 + 11 = 13. Это третий корень!
Решением исходного уравнения будет X1 = 2, X2 = - 5, X3 = 13.
Расчет закончен !
Пример 4 Решить уравнение с помощью формул системы mn параметров
x3 - 6.85x2 + 13.425x – 8.1 = 0
где a =1, b = - 6.85, c = 13.425, d = - 8.1
В этом уравнении имеют место нецелые значения коэффициентов. Это указывает на то, что и корни также могут иметь нецелые значения.
Решение
1. Определяем значение D1 = -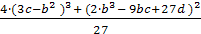
-→D1 = - [4( 40.275 – 46.9225)3+(- 642.83825 + 827.65125 – 218.7)2]/27
-→D1 = - [- 1174.9923236875+1148.328769]/27= 0.987539062500
2. Определяем значение D2 = - 2( 3c - )
-→ D2 = - 2(40.275 – 46.9225 ) = 13.2950
В этом случае имеют место дробные значения для D1 и D2 . Предлагаемый метод решения куб.уравнения оперирует только с целыми числами, поэтому необходимо умножить на 10k .
При этом значение степени k должно определяться
- для D2 числом знаков в мантиссе ( для данного примера k2 = 4 )
- для D1 = 3∙ (число знаков в мантиссе для D2 ). -→ k1 = 3∙ k2 ( для данного примера k1 = 12 ).
Для дальнейшего рассмотрения используем два числа
- D11 = 987539062500
- D21 = 132950.
3. Далее задача заключается в том, чтобы определить три значения таких целых чисел ( А,Б,Д), при которых выполняются равенства D21 = А2 + Б2 + Д2 и D11 = А2 ∙ Б2 ∙ Д2 .
Для нахождения значений чисел А,Б,Д можно использовать две методики
- найти все варианты представления числа D21 в виде суммы трех квадратов. При этом один