КУРСОВАЯ РАБОТА
"Неразрешимость логики первого порядка"
Введение формальный неразрешимость логика остановка
Философы сформулировали наиболее важные идеи искусственного интеллекта, но для преобразования его в формальную науку потребовалось достичь определенного уровня математической формализации в трех фундаментальных областях: логика, вычисления и вероятность.
Истоки идей формальной логики можно найти в работах философов древней Греции, но ее становление как математической дисциплины фактически началась с трудов Джорджа Буля (1815–1864), который детально разработал логику высказываний, или булеву логику. В 1879 году Готтлоб Фреге (1848–1925) расширил булеву логику для включения в нее объектов и отношений, создав логику первого порядка, которая в настоящее время используется как наиболее фундаментальная система представления знаний.
Одним из принципиально важных результатов математической логики является доказательство неразрешимости в логике первого порядка распознавания проблем как общезначимости, так и выполнимости ее предложений.
Цель исследования – изучить доказательства неразрешимости логики первого порядка. Для достижения данной цели необходимо выделить ряд задач:
1. Изучить основные понятия логики первого порядка.
2. Рассмотреть понятие машины Тьюринга и доказать неразрешимость проблемы остановки.
3. Вывести неразрешимость логики первого порядка из неразрешимости проблемы остановки.
4. Разобрать доказательство неразрешимости логики первого порядка методом Геделя.
1. Понятие формальной системы
Формальная система (или формальная теория) – результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.
Формальная теория считается определенной, если:
- задано конечное или счётное множество произвольных символов (конечные последовательности символов называются выражениями теории);
- имеется подмножество выражений, называемых формулами;
- выделено подмножество формул, называемых аксиомами;
- имеется конечное множество отношений между формулами, называемых правилами вывода.
Обычно имеется эффективная процедура, позволяющая по данному выражению определить, является ли оно формулой. Часто множество формул задаётся индуктивным определением. Как правило, это множество бесконечно. Множество символов и множество формул в совокупности определяют язык или сигнатуру формальной теории.
Чаще всего имеется возможность эффективно выяснять, является ли данная формула аксиомой; в таком случае теория называется эффективно аксиоматизированной или аксиоматической. Множество аксиом может быть конечным или бесконечным. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические или собственные аксиомы (определяющие специфику и содержание конкретной теории).
Для каждого правила вывода R и для каждой формулы A эффективно решается вопрос о том, находится ли выбранный набор формул в отношенни R с формулой A, и если да, то A называется непосредственным следствием данных формул по правилу R.
Выводом называется всякая последовательность формул такая, что всякая формула последовательности есть либо аксиома, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.
Формула называется теоремой, если существует вывод, в котором эта формула является последней.
Теория, для которой существует эффективный алгоритм, позволяющий узнавать по данной формуле, существует ли ее вывод, называется разрешимой; в противном случае теория называется неразрешимой.
Теория, в которой не все формулы являются теоремами, называется абсолютно непротиворечивой.
Дедуктивная теория считается заданной, если:
– задан алфавит (множество) и правила образования выражений (слов) в этом алфавите;
– заданы правила образования формул (правильно построенных, корректных выражений);
– из множества формул некоторым способом выделено подмножество T теорем (доказуемых формул).
Свойства дедуктивных теорий:
1. Противоречивость. Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой. Выяснение противоречивости теории – одна из важнейших и иногда сложнейших задач формальной логики. После выяснения противоречивости теория, как правило, не имеет дальнейшего ни теоретического, ни практического применения.
2. Полнота. Теория называется полной, если в ней для любой формулы F выводима либо сама F, либо ее отрицание. В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.
3. Независимость аксиом. Отдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима.
4. Разрешимость. Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс (алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет.
2. Основные понятия логики первого порядка Логика первого порядка (исчисление предикатов) – формальное исчисление, то есть это совокупность абстрактных объектов, не связанных с внешним миром, в котором представлены правила оперирования множеством символов в строго синтаксической трактовке без учета смыслового содержания.
Язык логики первого порядка строится на основе сигнатуры, состоящей из следующих символов:
1) логические
– символы логических операций ¬,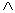 
, 
, ↔, →;
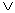– символы кванторных операций ", $;
– служебные символы: скобки и запятая.
2) нелогические
– множество предикатных символов, с которым связана арность, то есть число возможных аргументов P(n), Q(m), …, P1(n), P2(n);
– символы пропозициональных переменных X, Y, Z, …, X1, X2, … (можно считать, что символы пропозициональных переменных – это нульместные предикатные символы);
– символы предметных переменных x, y, z, …, x1, x2,…;
– символы предметных констант a, b, c, …, a1, a2, …
n-местным предикатом P (x1, x2,…, xn) называется функция P: M1ЧM2Ч…ЧMn → {1,0}, определенная на наборах длины n элементов некоторого множества M= M1ЧM2Ч…ЧMn и принимающая значения в области {1,0}. Множество М называется предметной областью предиката, его элементы – предметными константами.
Отрицанием предиката P(x1, x2,…, xn), определенного на множестве M1ЧM2Ч…ЧMn называется предикат ¬P(x1, x2,…, xn), определенный на том же множестве, который на наборе (a1, a2,…, an)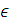 
M1ЧM2Ч…ЧMn
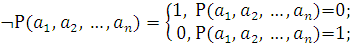
Конъюнкцией предикатов P(x1, x2,…, xn), определенного на множестве M1ЧM2Ч…ЧMn, и Q(y1, y2,…, ym), определенного на множестве N1ЧN2Ч…ЧNm, называется предикат P 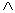Q(x1, x2,…, xn, y1, y2,…, ym) c пердметной областью M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn, который на наборе (a1, a2,…, an, b1, b2,…, bm) 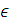M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn
$IMAGE7$
Дизъюнкцией предикатов P(x1, x2,…, xn), определенного на множестве M1ЧM2Ч…ЧMn, и Q(y1, y2,…, ym), определенного на множестве N1ЧN2Ч…ЧNm, называется предикат P 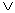Q(x1, x2,…, xn, y1, y2,…, yn) c пердметной областью M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn, который на наборе (a1, a2,…, an, b1, b2,…, bm) 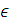M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn
$IMAGE10$
Импликацией предикатов P(x1, x2,…, xn), определенного на множестве M1ЧM2Ч…ЧMn, и Q(y1, y2,…, ym), определенного на множестве N1ЧN2Ч…ЧNm, называется предикат P → Q(x1, x2,…, xn, y1, y2,…, yn) c пердметной областью M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn, который на наборе (a1, a2,…, an, b1, b2,…, bm) 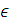M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn
$IMAGE12$
Эквивалентностью предикатов P(x1, x2,…, xn), определенного на множестве M1ЧM2Ч…ЧMn, и Q(y1, y2,…, ym), определенного на множестве N1ЧN2Ч…ЧNm, называется предикат P(x1, x2,…, xn) ↔ Q (y1, y2,…, yn) c пердметной областью M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn, который на наборе (a1, a2,…, an, b1, b2,…, bm) 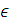M1ЧM2Ч…ЧMnЧN1ЧN2Ч…ЧNn
$IMAGE14$
Операцией связывания квантором общности переменной xi в n-местном предикате P(x1, x2,…, xn)), определенном на множестве M1ЧM2Ч…ЧMn, называется операция, в результате которой получается n-1-местный предикат " xi P(x1, x2,…, xi-1, xi+1,…, xn), который при значениях x1 = a1, …, xi-1 = ai-1, xi-1 = ai-1, …, xn = an истинен, если при любых значениях xi = ai высказывание P(a1, a2,…, an) истинно.
Операцией связывания квантором существования переменной xi в n-местном предикате P(x1, x2,…, xn) называется операция, в результате которой получается n-1-местный предикат $ xi P(x1, x2,…, xi-1, xi+1,…, xn), который при значениях x1 = a1, …, xi-1 = ai-1, xi-1 = ai-1, …, xn = an истинен, если при некотором значении xi = ai высказывание P(a1, a2,…, an) истинно.
Вхождение какой-либо переменной в формулу, называется свободным, если оно не входит в область действия никакого квантора по этой переменной.
Формулами логики предикатов являются:
– всякая нульместная предикатная переменная;
– P(n) (x1, x2,…, xn), где P(n) – n-местная предикатная переменная, а x1, x2,…, xn – свободные переменные;
– $IMAGE15$F, где F – формула;
– F1 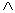F2, F1 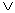F2, F1 ↔ F2, F1 → F2, где F1 и F2 – формулы, в которых общие переменные являются одновременно свободными или одновременно связанными;
– " xi P(x1, x2,…, xi-1, xi