Федеральное агентство по образованию Российской Федерации
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО
Кафедра дискретной математики
и информационных технологий
Курсовая работа
МОНОМИАЛЬНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
Студента 4 курса факультета КНиИТ
дневного отделения
Научный руководитель
доцент, к.ф.-м.н. Л.Б. Тяпаев
Зав. Кафедрой ДМиИТ
доцент, к.ф.-м.н. Л.Б. Тяпаев
Саратов 2010
СОДЕРЖАНИЕ
Введение
1. Теоретическая часть
1.1 Конечные динамические системы
1.2 Сокращение мономиальных систем
1.3 Линейные системы над конечными коммутативными кольцами.
Заключение
Список использованных источников
ВВЕДЕНИЕ
Важнейшая проблема в теории динамических систем заключается в том, чтобы связать структуру системы с её динамикой. В данной курсовой работе рассматривается такая связь для семейства нелинейных систем над произвольными конечными областями. Для систем, которые могут быть описаны мономами, можно получить информацию о конечной циклической структуре для структуры мономов. В частности, курсовая работа содержит достаточное условие для мономиальных систем, имеющих только фиксированные элементы, в качестве конечных циклов. Условие позволяет уменьшить проблему изучения Булевых мономиальных систем и линейных систем над конечными кольцами.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1 Конечные динамические системы
Конечные динамические системы – динамические системы с конечным набором состояний в дискретном времени. Широко известны примеры использование клеточного автомата и Булевой сети, они нашли широкое применение в машиностроении, в компьютерных науках, и, ещё раньше, в биологической статистике. Чаще общие многопозиционные системы используются в теории управления, в проектировании и анализе компьютерного моделирования. Основной математический вопрос, который обычно возникает в большинстве из этих наук – как анализировать динамику модели без фактического перечисления всех состояний переходов, так как перечисление имеет экспоненциальную сложность в количестве переменных в модели.
Для ответа на поставленный вопрос, обозначим конечную динамическую систему как функцию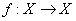 
, где 
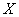– конечный набор. Динамика 
заключается в повторении и кодируется в его фазовом пространстве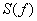 
, которое является ориентированным графом определённым следующим образом. Вершина 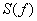– элемент из 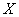. Существует ориентированная дуга $IMAGE8$ в 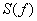если $IMAGE10$. В частности, допустима ориентированная дуга в саму себя. То есть 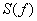кодирует все состояния переходов , и имеет свойство: для каждой вершины имеется полустепень исхода точно равная 1. Каждый компонент связанного графа 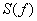состоит из направленного цикла, так называемого конечного цикла, с направленным деревом приложенным к каждой вершине в цикле, состоящем из так называемых переходов.
Любую Булеву сеть можно представить как конечную динамическую систему $IMAGE14$, где $IMAGE15$ – конечная область над двумя элементами и $IMAGE16$. В данной курсовой работе, изучаются конечные динамические системы $IMAGE17$, где $IMAGE18$ – любая конечная область и $IMAGE19$. Точнее, рассматривается семейство нелинейных конечных систем, для которых можно получить информацию относительно динамики структуры функции.
Пусть $IMAGE17$, $IMAGE16$ – конечная динамическая система. Рассмотрим, как может быть описана в зависимости от координатных функций $IMAGE23$, то есть, $IMAGE24$. Известно что любая теоретико-множественная функция $IMAGE25$ может быть представлена полиномиалом в $IMAGE26$. Этот полиномиал может быть выбран таким образом, чтобы любая переменная в нём была в степени меньшей чем $IMAGE27$. То есть, для любого $IMAGE28$ имеется уникальное $IMAGE29$, такое что $IMAGE30$ для всех $IMAGE31$. Следовательно, любая конечная динамическая система над конечной областью может быть представлена как полиномиальная система.
В случае, где все $IMAGE32$ – линейные полиномиалы без константного описания, динамику линейных систем можно полностью определить ее матричным представлением. Пусть $IMAGE34$ – матричное представление линейной системы $IMAGE17$. Тогда количество конечных циклов и их длинна, так же как структура переходов, может быть определена разложением на множители характерной полиномиальной матрицы $IMAGE34$. Структура конечных циклов была определена ранее Элспасом, и для аффинных систем Миллиганом и Уилсоном.
В данной курсовой работе рассматривается класс нелинейных систем, описанных специальным типом полиномиалов, а именно мономами. То есть, рассматриваются системы $IMAGE37$, такие, что каждый $IMAGE32$ был полиномиалом вида $IMAGE39$, или константой. Допустимо предположение, что никакая координатная функция не константа, так как это частный случай переменной. Некоторые классы мономиальных систем и их динамические поведения изучались прежде в работах: Мономы клеточного автомата, Булевы мономиальные системы, мономиальные системы над периодическими числами и мономиальные системы над конечными областями.
В работе «Булевы мономиальные системы» изучался специальный класс Булевых мономиальных систем, а именно те, которые имеют фиксированные элементы в качестве конечных циклов, так называемые системы конечных элементов. Причиной для рассмотрения именно этого класса стало использование полиномиальных систем в качестве моделей для биохимических сетей. В зависимости от экспериментально рассматриваемой системы, такие сети часто проявляют устойчивые состояния динамики. То есть, их динамические модели имеют фазовые пространства, в которых конечные циклы – фиксированные элементы. С целью подбора модели, было бы полезно иметь структурный критерий распознания фиксированных элементов системы. Главная цель данной работы ответить на вопрос о мономиальных системах над общей конечной областью $IMAGE18$, а так же, на вопрос о связи Булевой мономиальной системы и линейной системы над кольцом $IMAGE41$.
1.2 Сокращение мономиальных систем
Пусть $IMAGE24$: $IMAGE43$ – полиномиальная система, где каждый $IMAGE32$ – моном, такой, что $IMAGE45$, где $IMAGE46$ – неотрицательное целое число. То есть, может быть описано матрицей $IMAGE48$. В первую очередь связывается с Булевой мономиальной системой $IMAGE50$ и линейной системой $IMAGE51$ над кольцами $IMAGE52$. В работе «Булевы мономиальные системы» называется системой конечных элементов если все конечные циклы заключаются в фиксированном элементе. Покажем что – конечный элемент системы тогда, и только тогда, когда $IMAGE50$ и $IMAGE51$ – системы конечных элементов.
Определение 1.2.1.
Для $IMAGE58$, мы определим базис $IMAGE59$, обозначенный supp(u), равный $IMAGE60$, где
$IMAGE61$ $IMAGE62$ $IMAGE63$
Мономиальная система $IMAGE24$ порождает Булеву мономиальную систему $IMAGE65$ на $IMAGE66$ с параметрами $IMAGE67$, где $IMAGE68$ и v=supp(u).
Лемма 1.2.1.
$IMAGE69$- коммутативная диаграмма.
Доказательство.
Это прямо доказывается тем что supp(f(u))=f(supp(u)).
Так как $IMAGE70$ на множестве всех $IMAGE59$ таких, что supp(u)=u, появляется следующие прямые следствия.
Следствие 1.2.1.
Фазовое пространство $IMAGE50$ – подграф фазового пространства .
Следствие 1.2.2.
Предположим что $IMAGE50$ – система конечных элементов. Если $IMAGE75$ – цикл в фазовом пространстве , тогда $IMAGE77$ для всех $IMAGE78$.
Пример 1.2.1.
Пусть $IMAGE79$.
$IMAGE80$- состоит из всех возможных наборов длины 3 из трёх элементов: 0, 1, 2.
Это наборы:
$IMAGE81$
Используя функцию $IMAGE79$, определим переходы в фазовом пространстве .
000 - $IMAGE84$,
001 - $IMAGE85$,
002 - $IMAGE86$,
010 - $IMAGE87$,
020 - $IMAGE88$,
100 - $IMAGE89$,
200 - $IMAGE90$,
111 - $IMAGE91$,
110 - $IMAGE92$,
112 - $IMAGE93$,
101 - $IMAGE94$,
121 - $IMAGE95$,
011 - $IMAGE96$,
211 - $IMAGE97$,
222 - $IMAGE98$,
220 - $IMAGE99$,
221 – $IMAGE100$,
202 - $IMAGE101$,
212 - $IMAGE102$,
022 - $IMAGE103$,
122 - $IMAGE104$,
012 - $IMAGE105$,
021 - $IMAGE106$,
210 - $IMAGE107$,
102 - $IMAGE108$,
120 - $IMAGE109$,
210 - $IMAGE110$,
201 - $IMAGE111$,
Так как $IMAGE112$, то $IMAGE113$. Используя эту функцию, определим переходы в фазовом пространстве $IMAGE50$.
000 - $IMAGE115$,
001 - $IMAGE116$,
010 - $IMAGE117$,
100 - $IMAGE118$,
101 - $IMAGE119$,
011 - $IMAGE120$,
110 - $IMAGE121$,
111 - $IMAGE122$.
На рисунке 1.2.1 и 1.2.2 изображены фазовое пространство системы и ее «Булеанизяция» $IMAGE50$, соответственно.
$IMAGE125$
Рис. 1.2.1. Фазовое пространство .
$IMAGE127$
Рис. 1.2.2. Фазовое пространство $IMAGE50$.
Затем связывается с $IMAGE130$ - размерной линейной системой над конечным кольцом. Заметим сначала что $IMAGE131$ – изоморфный, как Абелева группа, для $IMAGE41$ через изоморфизм $IMAGE133$, появляется возможность генератора для циклической группы $IMAGE134$. В первую очередь обратим внимание, что множество векторов $IMAGE135$ со всеми ненулевыми вхождениями – постоянны для .
Пусть $IMAGE137$ – генератор для циклической группы $IMAGE138$,и пусть $IMAGE139$.
Тогда $IMAGE140$.
Определение 1.2.2.
Обозначим $IMAGE141$ для $IMAGE142$.
Видно что $IMAGE51$ – линейное преобразование $IMAGE144$- элемента. Но можно рассматривать его, как линейное преобразование для $IMAGE145$ - элемента, рассматривая $IMAGE145$ как конечное кольцо, которое обозначим – $IMAGE147$. То есть, имеется линейное преобразование $IMAGE148$.
Это доказывает следующую лемму.
Лемма 1.2.2.
$IMAGE149$ - коммутативная диаграмма.
Обратим внимание, что вертикальные стрелки – изоморфизмы. Это значит, что они сохраняют фазовое пространство структуры, включая длину конечных циклов. В частности, имеется следующее следствие.
Следствие 1.2.3.
Фазовое пространство $IMAGE51$ изоморфно к подграфу фазового пространства , состоя из всех наборов с базисным вектором $IMAGE152$.
Пример 1.2.2.
Для мономиальной системы в примере 1.2.1, $IMAGE154$ определим $IMAGE155$, где
$IMAGE156$.
Рассчитаем переходы в фазовом пространстве $IMAGE51$.
000 - $IMAGE158$,
001 - $IMAGE159$,
010 - $IMAGE160$,
011 - $IMAGE161$,
100 - $IMAGE162$,
101 - $IMAGE163$,
110 - $IMAGE164$,
111 - $IMAGE165$.
Фазовое пространство $IMAGE51$ изображено на рисунке 1.2.3.
$IMAGE167$
Рис. 1.2.3. Фазовое пространство $IMAGE51$.
Теорема 1.2.1.
Пусть $IMAGE17$ – мономиальная динамическая система. Тогда – система конечных элементов тогда, и только тогда, когда $IMAGE50$и $IMAGE51$ – системы конечных элементов.
Доказательство.
Из следствий 1.2.1 и 1.2.3, если – система конечных элементов, то $IMAGE50$ и $IMAGE51$ тоже системы конечных элементов. Для доказательства от противного, предположим что $IMAGE51$ и $IMAGE50$ – системы конечных элементов, а – нет. Для каждого конечного цикла , любой из двух связанных наборов имеет все координаты ненулевые, или все наборы имеют минимум одну нулевую координату. В первом случае из этого следует, что $IMAGE51$ имеет конечный цикл, той же длины. Следовательно, если имеет конечный цикл длины большей чем $IMAGE182$, тогда включаются только наборы имеющие минимум одну нулевую координату.
Пусть $IMAGE183$ – наборы в конечном цикле. Так как этот конечный цикл должен отображать конечный элемент для $IMAGE50$ из этого следует, что $IMAGE185$ имеет тот же самый базисный вектор, то есть, тот же самый образец нулевых вхождений, и отличается только в ненулевых координатах. Кроме того, мономы в ненулевых координатах не включают никакие переменные, соответствующие нулевым координатам. Таким образом, если построить новый набор $IMAGE186$, заменяя каждый $IMAGE187$ в $IMAGE185$, на $IMAGE182$, $IMAGE186$ – будет частью конечного цикла длины, по крайней мере $IMAGE191$, что является противоречием. Это доказывает теорему.
1.3 Линейные системы над конечными коммутативными кольцами
Теорема в предыдущей части показывает что для того чтобы решить, будет ли данная мономиальная система , над конечной областью $IMAGE18$, системой с конечными элементами, достаточно решить этот вопрос для связанных булевых систем, для которых определена линейная система над конечным кольцом $IMAGE194$. Поэтому остаётся развить критерий для линейных систем над конечными коммутативными кольцами, для того чтобы решить б