БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Курсовая работа
Дисциплина «Математическое моделирование»
Тема: «Моделирование движения парашютиста»
Минск 2008
Содержание
Введение
1. Свободное падение тела с учетом сопротивления среды
2. Формулировка математической модели и ее описание.
3. Описание программы исследования с помощью пакета Simulink
4. Решение задачи программным путем
Список использованных источников
Введение
Формулировка проблемы:
Катапульта выбрасывает манекен человека с высоты 5000 метров. Парашют не раскрывается, манекен падает на землю. Оценить скорость падения в момент удара о землю. Оценить время достижения манекеном предельной скорости. Оценить высоту, на которой скорость достигла предельного значения. Построить соответствующие графики, провести анализ и сделать выводы.
Цель работы: Научиться составлять математическую модель, решать дифференциальные уравнения программными средствами (используется язык технических вычислений MatLAB 7.0, пакет расширения Simulink) и анализировать полученные данные о математической модели.
1. Свободное падение тела с учетом сопротивления среды При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, 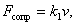 где
где 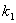 определяется свойствами среды и формой тела. Например, для шарика
определяется свойствами среды и формой тела. Например, для шарика 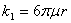 — это формула Стокса, где
— это формула Стокса, где 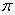 — динамическая вязкость среды, r — радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм
— динамическая вязкость среды, r — радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм 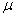 = 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2.
= 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (в движение станет равномерным).
Имеем
$IMAGE6$
или
$IMAGE7$ (1)
Пусть r= 0,1 м, $IMAGE8$= 0,8 кг/м (дерево). При падении в воздухе $IMAGE9$ м/с, в воде $IMAGE10$17 м/с, в глицерине $IMAGE10$0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: $IMAGE12$. Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если $IMAGE13$, то вкладом $IMAGE14$ можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды $IMAGE15$ и зависит от формы тела. Обычно представляют k2 = 0,5сS $IMAGE15$, где с — коэффициент лобового сопротивления — безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис.1.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается. Для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
Имеем
$IMAGE17$
или
$IMAGE18$ (2)
для шарика
$IMAGE19$ (3)
| $IMAGE20$ | Диск Полусфера Полусфера Шар Каплевидное тело Каплевидное тело | с = 1,11 с = 1,33 с = 0,55 с = 0,4 с = 0,045 с = 0,01 |
Рис 1. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Примем r = 0,1 м, $IMAGE8$=0,8.103 кг/м3 (дерево). Тогда для движения в воздухе ( $IMAGE22$= 1,29 кг/м3 ) получаем $IMAGE23$ $IMAGE24$18 м/с, в воде( $IMAGE25$= 1.103 кг/м3 ) $IMAGE23$ $IMAGE24$0,65 м/с, в глицерине ( $IMAGE28$= 1,26.103 кг/м3 ) $IMAGE23$ $IMAGE24$ 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения — уравнение второго закона Ньютона с учетом двух сил, действующих на тело: силы тяжести и силы сопротивления среды:
$IMAGE31$ (4)
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
$IMAGE32$ (5)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7) заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, $IMAGE33$, и соответствующую установившуюся скорость $IMAGE34$можно найти из условия $IMAGE35$=0, решая не дифференциальное, а квадратное уравнение. Имеем
$IMAGE36$ (6)
(второй — отрицательный — корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от $IMAGE37$ до $IMAGE38$. Как и по какому закону – это можно узнать, лишь решив дифференциальное уравнение (7).
Однако даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. И хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны. Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций – а как найти закон изменения во времени перемещения? Формальный ответ прост:
$IMAGE39$ (7)
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно обычна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т. е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс - а именно это есть цель моделирования.
В достижении этой цели компьютер — незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, — задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения $IMAGE40$ и $IMAGE41$, найденные компьютером, следует записывать в результирующую таблицу (табл. 2).
Таблица 2
Зависимость перемещения и скорости падения от времени (от 0 до 15 с)
| t(c) | S(m) | $IMAGE40$(м/с) | t(c) | S(m) | $IMAGE40$(м/с) |
| 0 1 2 3 4 5 6 7 | 0 4.8 18.7 40.1 66.9 97.4 130.3 164.7 | 0 9,6 17,9 24,4 28,9 31,9 33,8 35,0 | 8 9 10 11 12 13 14 15 | 200.1 235.9 272.1 308.5 345.0 381.5 418.1 454.7 | 35.6 36.0 36.3 36.4 36.5 36.6 36.6 36.6 |
Кроме таблицы необходимы графики зависимостей $IMAGE44$ и $IMAGE45$; по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске — приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом — скажем, через каждый метр или каждые 100 метров — смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии зд