База рефератов

СОДЕРЖАНИЕ

Введение

1. Многочлены Лежандра

2. Многочлены Чебышева

3. Преобразование Лапласа

4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке

4.1 Постановка задачи

4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра

4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.

Заключение

преобразование смещенный многочлен исчисление

ВВЕДЕНИЕ

Математический анализ – раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела.

Начало математическому анализу положил в 1665 И.Ньютон и (около 1675) независимо от него Г.Лейбниц, хотя важную подготовительную работу провели И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма (1601–1665), Дж.Валлис (1616–1703) и И.Барроу (1630–1677).

Операционное исчисление – раздел математики, занимающийся главным образом алгебраическими операциями, производимыми над символами операции (или преобразования).

Во многих задачах математического анализа рассматриваются ситуации, в которых каждая точка одного пространства ставится в соответствие некоторой точке другого (или того же) пространства. Пространства могут быть абстрактными, в которых «точки» в действительности являются функциями. Соответствие между двумя точками устанавливается с помощью преобразования или оператора. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления. Обычно теорию операторов применяют к пространствам, в которых допускается сложение или умножение точек, т.е. линейным пространствам, группам, кольцам, полям и т.д.

Операционное исчисление позволяет осуществить абстрактные постановки задач и обобщить такие разделы математического анализа, как теория дифференциальных и интегральных уравнений. Мощным стимулом для развития теории операторов стали современные проблемы квантовой теории. Наиболее полные результаты получены для дистрибутивных операторов в т.н. гильбертовом пространстве. Интерес к этой области во многом связан с представлением таких операторов интегральными преобразованиями.

В середине XIX века появился ряд сочинений, посвящённых так называемому символическому исчислению и применению его к решению некоторых типов линейных дифференциальных уравнений. Сущность символического исчисления состоит в том, что вводятся в рассмотрение и надлежащим образом интерпретируются функции оператора дифференцирования.

.

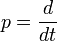Среди сочинений по символическому исчислению следует отметить вышедшую в 1862 году в Киеве обстоятельную монографию русского математика М. Е. Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений». В ней поставлены и разрешены основные задачи того метода, который в дальнейшем получил название операционного.

В 1892 году появились работы английского учёного О. Хевисайда, посвящённые применению метода символического исчисления к решению задач по теории распространения электрических колебаний в проводах.

В отличие от своих предшественников, Хевисайд определил обратный оператор однозначно, полагая и считая f(u) = 0 для u < 0. Труды Хевисайда положили начало систематическому применению символического, или операционного, исчисления к решению физических и технических задач.

Однако широко развитое в трудах Хевисайда операционное исчисление не получило математического обоснования, и многие его результаты оставались недоказанными. Строгое обоснование было дано значительно позже, когда была установлена связь между функциональным преобразованием Лапласа и оператором дифференцирования

 

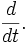
если существует производная , для которой

$IMAGE6$

существует и f(0) = 0, то

$IMAGE7$.

Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований. Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач теории упругости, теплопроводности, электродинамики и других разделов математической физики. Использование интегральных преобразований позволяет свести дифференциальное, интегральное или интегро-дифференциальное уравнение к алгебраическому, а также, в случае дифференциального уравнения в частных производных, уменьшить размерность.

Интегральные преобразования задаются формулой

$IMAGE8$, (1)

где функции $IMAGE9$ называются оригиналом и изображением соответственно, и являются элементами некоторого функционального пространства $IMAGE10$, при этом функция $IMAGE11$ называется ядром интегрального преобразования.

Большинство интегральных преобразований являются обратимыми, то есть по известному изображению можно восстановить оригинал, зачастую также интегральным преобразованием:

$IMAGE12$ (2)

Хотя свойства интегральных преобразований достаточно обширны, у них довольно много общего.

преобразование смещенный многочлен исчисление

1. Многочлены Лежандра

Многочлены Лежандра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке $IMAGE13$по мере Лебега. Многочлены Лежандра могут быть получены из многочленов $IMAGE14$ортогонализацией Грама ― Шмидта.

Названы по имени французского математика Адриен Мари Лежандра.

Многочлены Лежандра определяются по формуле (называемой формулой Родрига)

$IMAGE15$ (3)

часто записываемой в виде:

$IMAGE16$ (4)

Многочлены Лежандра также определяются по следующим формулам:

$IMAGE17$

$IMAGE18$

$IMAGE19$, если $IMAGE20$;

$IMAGE21$, если $IMAGE22$.

Они также могут быть вычислены по рекуррентной формуле:

$IMAGE23$

Первые многочлены Лежандра равны:

$IMAGE24$

$IMAGE25$

$IMAGE26$

$IMAGE27$

$IMAGE28$

$IMAGE29$

$IMAGE30$

$IMAGE31$

$IMAGE32$

$IMAGE33$

$IMAGE34$

2. Многочлены Чебышева

Многочлены Чебышева — две последовательности многочленов T_n(x) и U_n(x), $IMAGE35$названные в честь Пафнутия Львовича Чебышева.
Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода используются в качестве узлов в интерполяции алгебраическими многочленами.

Многочлен Чебышева первого рода T_n(x) характеризуется как многочлен степени n со старшим коэффициентом 2^{n - 1}, который меньше всего отклоняется от нуля на интервале [ − 1,1]. Впервые рассмотрены самим Чебышёвым.

Многочлены Чебышева первого рода T_n(x) могут быть определены с помощью рекуррентного соотношения:

$IMAGE36$

$IMAGE37$

$IMAGE38$

Многочлены Чебышева первого рода $IMAGE39$могут быть также определены с помощью равенства:

$IMAGE40$

или, что почти эквивалентно,

$IMAGE41$

Несколько первых многочленов Чебышева первого рода

$IMAGE42$

$IMAGE43$

$IMAGE44$

$IMAGE45$

$IMAGE46$

$IMAGE47$

$IMAGE48$

$IMAGE49$

$IMAGE50$

$IMAGE51$

Многочлены Чебышева обладают следующими свойствами:

Ортогональность по отношению к соответствующим скалярному произведению (с весом $IMAGE52$для многочленов первого рода и $IMAGE53$для многочленов второго рода).

Среди всех многочленов, значения которых на отрезке [ − 1,1] не превосходят по модулю 1, многочлен Чебышева имеет: наибольший старший коэффициент наибольшее значение в любой точке за пределами [ − 1,1] если $IMAGE54$, то $IMAGE55$, где t_k — коэффициент многочлена Чебышева первого рода, a_k — коэффициент любого из рассматриваемых полиномов.

Нули полиномов Чебышева являются оптимальными узлами в различных интерполяционных схемах. Например, в методе дискретных особенностей, который часто используется при исследовании интегральных уравнений в электродинамике и аэродинамике.

3.

4. Преобразование Лапласа

Преобразование Лапласа — интегральное преобразование, связывающее функцию $IMAGE56$комплексного переменного (изображение) с функцией $IMAGE57$действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Интеграл Лапласа имеет вид:

$IMAGE58$ (5)

где интегрирование производится по некоторому контуру L_в плоскости комплексного переменного z, ставящий в соответствие функции f(z), определенной на L, аналитическую функцию F(p) комплексного переменного p=s+it. Многие интегралы вида (5) были рассмотрены П. Лапласом.

В узком смысле под преобразованием Лапласа подразумевают одностороннее преобразование Лапласа

$IMAGE59$, (6)

называемое так в отличие от двустороннего преобразования Лапласа

  $IMAGE60$ (7)

Преобразование Лапласа –  частный вид интегральных преобразований;. преобразования вида (6) или (7) тесно связаны с Фурье преобразованием. Двустороннее преобразование Лапласа (7) можно рассматривать как преобразование Фурье функции $IMAGE61$, одностороннее преобразование Лапласа (6) - как преобразование Фурье функции j(t) равной $IMAGE61$ при 0 < t < ∞ и равной нулю при -∞ < t < 0.

Подынтегральная комплексная локально суммируемая функция f(t) называется функцией-оригиналом, или просто оригиналом; в приложениях часто удобно трактовать переменное t как время. Функция F(p)=L[f], (р) называется также преобразованием Лапласа оригинала f(t) или изображением по Лапласу. Интеграл (6) понимается, вообще говоря, как условно сходящийся на бесконечности.

Априори возможны три случая:

1) существует действительное число $IMAGE63$ такое, что интеграл (6) сходится при $IMAGE64$, а при $IMAGE65$ –  расходится; это число σ_с называется абсциссой (условной) сходимости;

2) интеграл (6) сходится при всех р, в этом случае полагают $IMAGE66$;

3) интеграл (6) расходится при всех р, в этом случае полагают $IMAGE67$ 

Если $IMAGE68$, то интеграл (6) представляет однозначную аналитическую функцию F(p) в полуплоскости сходимости $IMAGE69$.  Обычно ограничиваются рассмотрением абсолютно сходящихся интегралов (6). Точная нижняя грань тех s, для которых существует интеграл  $IMAGE70$, называется абсциссой абсолютной сходимости $IMAGE71$  $IMAGE72$ 

Если а – есть нижняя грань тех s, для которых $IMAGE73$ число а иногда называют показателем роста оригинала f(t).

При некоторых дополнительных условиях оригинал f(t) однозначно восстанавливается по своему F(p). Например, если f(t) имеет ограниченную вариацию в окрестности точки t₀ или если f(t) кусочногладкая, то имеет место формула обращения преобразования Лапласа:

$IMAGE74$ (8)

Формулы (6) и (8) позволяют получить ряд соотношений между операциями, производимыми над оригиналами и изображениями, а также таблицу изображений для часто встречающихся оригиналов. Все это составляет элементарную часть операционного исчисления.

В математической физике важные применения находит многомерное преобразование Лапласа:

$IMAGE75$ (9)

где t = (t₁, ……, t_n)

-точка re-мерного евклидова пространства

Rⁿ, p = (p₁, ……, p_n) = σ + iτ = (σ₁, ……, σ_n) + (τ₁, ……, τ_n)

-точка комплексного пространства

Cⁿ, n≥1, (p,t) = (σ,t)+i(τ,t) = p₁t₁ + … +p_nt_n

-скалярное произведение, dt = dt₁