Контрольная работа
«Методы оптимизации при решении уравнений»
Задание №1
Определить, существует ли кривая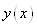 
, доставляющая функционалу экстремум и, если существует, то найти ее уравнение.
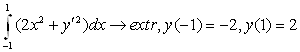
Решение: Составим уравнение Эйлера и найдём его общее решение:
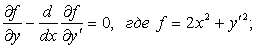
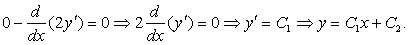
Используем краевые условия:
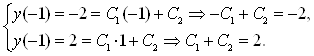
Решаем систему уравнений и получаем:
$IMAGE6$
Таким образом, экстремаль имеет уравнение вида
$IMAGE7$
Так как
$IMAGE8$
то функционал на прямой $IMAGE7$ достигает минимума.
Задание №2
Найти, используя уравнение Эйлера-Лагранжа, оптимальное управление $IMAGE10$, минимизирующее функционал $IMAGE11$ для системы, описываемой уравнениями
$IMAGE12$,
при начальных и конечных условиях соответственно:
$IMAGE13$
| A | B | t0 | tf | x0 | xf | a | b |
| 0 1 0 0 | 0 1 | 0 | 1 | 1 0 | 0 0 | 0 | 1 |
Решение
Формируем задачу по исходным данным:
$IMAGE14$ (1)
$IMAGE15$ (2)
$IMAGE16$
Составим функцию Лагранжа и гамильтониан:
$IMAGE17$
и соответственно уравнения Эйлера-Лагранжа (здесь для Н):
$IMAGE18$ (3)
$IMAGE19$ (4)
Используя замену (3), подставим выражения (4) во второе уравнение динамики в (1):
$IMAGE20$ $IMAGE21$
и находим общее решение
$IMAGE22$ (5)
Подставим его в первое уравнение (1):
$IMAGE23$
и находим общее решение:
$IMAGE24$ (6)
Для $IMAGE25$ из (6) и $IMAGE26$ из (5) используем начальные и конечные условия и получаем систему уравнений для констант С1, С2, С3, С4,:
$IMAGE27$
Таким образом, решение имеет вид:
$IMAGE28$
которое удовлетворяет начальным и конечным условиям.
Задание №3
Для системы, описываемой уравнениями
$IMAGE12$
с заданными условиями на начальное $IMAGE30$ и конечное $IMAGE31$ значение координат, найти оптимальное управление $IMAGE10$, минимизирующее функционал
$IMAGE33$
| A | B | t0 | tf | x0 | xf | g0 | a | b |
| 0 1 0 0 | 0 1 | 0 | t | 1 0 | x1(tf) = -tf2 | 0 | 0 | 1 |
Решение. Формулируем задачу по исходным данным
$IMAGE34$ (1)
$IMAGE35$ (2)
т.е. $IMAGE36$, подвижна на правом конце, координата $IMAGE37$ - свободна на правом конце,
$IMAGE38$
Составим функцию Гамильтона Н (или функцию Лагранжа L)
$IMAGE39$ (3)
и соответствующие уравнения Эйлера-Лагранжа:
$IMAGE40$ (4)
$IMAGE41$ (5)
$IMAGE42$ (6)
Составим вспомогательную функцию
$IMAGE43$,
где $IMAGE44$. Таким образом:
$IMAGE45$. (7)
Поскольку $IMAGE46$ и $IMAGE47$ подвижны, то используем условия трансверсальности:
$IMAGE48$
$IMAGE49$ (8)
$IMAGE50$ (9)
Так как не фиксирован момент времени $IMAGE51$, то используем условие трансверсальности
$IMAGE52$
Найдем значение $IMAGE53$ при $IMAGE54$ из (3), но учтем, что $IMAGE55$, а $IMAGE56$ из (9). Тогда, учитывая (4):
$IMAGE57$
и используя (10) получим:
$IMAGE58$ (11)
Подставляя (4), (5) и (6) в (2), а потом в (1) и интегрируя получим:
$IMAGE59$ (12),
$IMAGE60$ (13)
Используя начальные условия, можем записать:
$IMAGE61$
Запишем условие $IMAGE62$ с учетом (13). Тогда:
$IMAGE63$ (14)
Уравнения (9), (11) и (14) составляют систему уравнений с тремя неизвестными С1, С2 и $IMAGE64$:
$IMAGE65$
Подставляя 1-е уравнение во 2-е, получим:
$IMAGE66$,
а подставляя 1-е в третье, получим:
$IMAGE67$
Таким образом, решение имеет вид:
$IMAGE68$
Задание №4
Используя метод динамического программирования найти оптимальное уравнение для системы
$IMAGE69$
| A | B | t0 | tf | F | a | b |
| 0 1 0 0 | 0 1 | 0 | ∞ | 0 | 1 0 0 2 | 1 |
Решение:
Формируем задачу по исходным данным.