Метод Винера-Хопфа и его приложения в физических задачах.
Демидов Р.А. ,ФТФ, 2105
Введение
Указанный метод подходит для решения интегральных уравнений на полубесконечном промежутке с ядром, зависящим от разности аргументов – речь идет об уравнениях вида
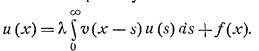 .
.
Этот метод был предложен в совместной работе Н.Винера и Э.Хопфа в 1931 году, и находит разнообразные применения в теории дифференциальных и интегральных уравнений, а также в их приложениях в физических задачах.
В своей работе я опишу сам метод Винера-Хопфа, а также приведу его применение к решению краевых задач матфизики.
1. Метод
1.1 Случай бесконечного промежутка
Метод Винера-Хопфа основан на специальном виде ядра интегрального уравнения – оно зависит от разности аргументов, а не от самого аргумента. Собственно, для начала рассмотрим уравнение вида
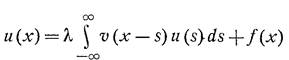 (1)
(1)
- это уравнение с бесконечным промежутком и тем же самым ядром. Решение его существует ,если выполняются 2 условия:
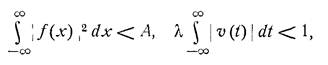 ,
,
а также условие сходимости нормы u(x):
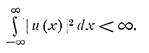 .
.
Эти условия работают при действительных λ. Мы рассмотрим два способа решения этого уравнения – один, использующий свойство свертки напрямую, другой – с помощью резольвенты. Итак,первый.Заметим, что в случае именно бесконечного промежутка интеграл представляет собой свертку ядра и функции u(x). Вспомнив,что Фурье-образы функций u(x),f(x),g(x) выглядят как, воспользуемся свойством образа свертки двух функций – “образ свертки есть свертка образов”.Тогда для функций U(k),V(k),F(k) – образов соответствующих функций, получаем алгебраическое уравнение:
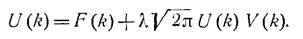 (2)
(2)
$IMAGE6$
Данное свойство образа свертки доказывается “в лоб”, а именно – домножением равенства (1) на $IMAGE7$и интегрированием по всей действительной оси:
$IMAGE8$
Делая замену во втором интеграле (x-s)=t, получаем
$IMAGE9$,
что и требовалось доказать.
Видим, что мы свели исходную задачу к алгебраическому уравнению относительно образа исходной функции u(x). Выражая его через образы ядра и f(x),производя обратное преобразование Фурье, получаем в качестве искомого решения:
$IMAGE10$ =>
=> $IMAGE11$ $IMAGE12$(3)
Второй способ: вычисляем резольвенту уравнения как
$IMAGE13$ (4)
В виде Фурье - образов это равенство выглядит так:
$IMAGE14$,
где G(k) вычисляется как
$IMAGE15$ (5)
V(k) – Фурье-образ исходного ядра v(x) уравнения (1).То есть для решения исходного уравнения необходимо найти функцию g(x),применив обратное преобразование Фурье к (5),и подставить его в (4). Этот способ не требует вычисления каждый раз интегралов для F(k) при смене функции f,она подставляется в самом конце один раз, поэтому такой способ быстрее.
На примере этой задачи мы поняли, как решать уравнение с бесконечным промежутком интегрирования. На этом примере мы будем строить решение уравнения с полубесконечным промежутком – и опишем метод Винера-Хопфа.
1.2 Полубесконечный промежуток
Понятно, что в случае, если интегрирование идет не с -∞, а с 0, переходя к образам, мы не можем воспринимать наш интеграл как свертку – а значит, и не можем написать наше уравнение. Запишем некоторые свойства преобразования Фурье, связанные с полубесконечными промежутками, которые нам понадобятся в дальнейшем. Итак, в случае разбиения функции f (x) на два куска – f+(x) и f-(x), (f(x)= f+(x) + f-(x) )представляющих собой правый и левый концы следующим образом:
$IMAGE16$
выражения для прямых и обратных преобразований Фурье для них будет выглядеть так:
f+: $IMAGE17$,
при $IMAGE18$причем здесь $IMAGE19$- комплексная переменная, и выполняется неравенство Im(k)=τ > τ- . Причем
$IMAGE20$
Обратное преобразование выглядит так:
$IMAGE21$,
и здесь мы интегрируем по любой прямой Im(k)=τ > τ- .
f-: При $IMAGE22$
для прямого преобразования Фурье имеем
$IMAGE23$,
к здесь та же к.п. ,это верно в области с Im(k)=τ < τ+ . Обратное преобразование для f- выглядит аналогично:
$IMAGE24$
Интегрирование идет по той же прямой с Im(k)=τ < τ+
При τ- < τ+ образ F(k) задаётся уравнением
$IMAGE25$
как раз в полосе τ- < Im(τ) < τ+ . При τ- < 0,τ+ > 0 функция полоса Im(τ)=0 попадает в границы интегрирования, и интеграл можно взять вещественным, выбрав мнимую часть τ нулем.
Применим эти соображения к решению искомого уравнения. (6)
$IMAGE26$(6)
Разложим неизвестную функцию u(x) на составляющие u+ , u- :
$IMAGE27$
$IMAGE28$
При подстановке этих функций в уравнение (6) мы получаем два уравнения на каждую часть u(x).Факт существование решения мы примем без доказательств. Мы ищем решения, удовлетворяющие следующим условиям:
$IMAGE29$,
$IMAGE30$µ<τ+.
При их выполнении в полосе µ < Im(k) < τ+ функции u+ ,u- являются аналитическими.
Переходя по формулам преобразования Фурье к уравнению для образов, аналогично проделанному в §1,мы имеем право пользоваться теми же свойствами, по причине именно такого выбора функций u+ ,u- .Итак, получаем:
$IMAGE31$ ,
что видно из представления u(x)= u+(x)+u-(x), U(k)=U+(k)+U-(k) и уравнения (6).Перенося все в левую часть, видим, что
$IMAGE32$,
если так задать функцию L(k).
$IMAGE33$
Мы подошли к сути метода Винера-Хопфа: путем преобразования Фурье свели наше уравнение к алгебраическому, но уже относительно образов функции. Однако в нашем случае, в отличие от §1,неизвестныхфункций в нем две, и обе нам нужны. Грубо говоря, нам позволено найти решение, но оно не будет однозначным, и данный метод работает лишь для определенного вида функций.Пусть мы нашу функцию L(k) можем представить как частное функций L+(k),L-(k),уравнение принимает при этом вид
$IMAGE34$,
и известно следующее – “плюсовая” часть есть аналитическая функция к.п. в области $IMAGE35$, “минусовая” часть аналитическая функция в области $IMAGE36$,µ <τ+ , а значит, в полосе $IMAGE37$ (которая непуста )существует единственная общая функция U(k), совпадающая с U+ ,U- в соответствующих областях. Если дополнительно задать, что функции L+,L- растут не быстрее степенной функции kn, то функции можем считать определенными, и приравнять правую и левую часть в общем случае многочлену Pn(k) (это получается, если учесть стремление U+,U- к нулю по |к|-> ∞.Теперь у нас неопределенности нет, и в общем виде это выглядит так:
Если степень роста функций L есть единица(растут не быстрее линейной функции),то мы имеем для кусков функции L(k) следующее:
$IMAGE38$,
и в итоговом решении будет присутствовать произвольная константа C.Приведу пример последнего случая с n=0. Пример.
$IMAGE39$
- интегральное уравнение с полубесконечным промежутком и нулевой f для простоты. Решим его м.В.-Х.
Как видим, мы имеем дело с ядром вида exp(-|x|).Найдем его Фурье-образ, и далее, функцию L(k):
$IMAGE40$
$IMAGE41$
- является аналитической в области -1 < Im(k) < 1. Разложим ее как частное двух так:
$IMAGE42$
При 0 < λ < 0.5 условия одновременной аналитичности выполняются в полосе µ < Im(k) < 1, при λ > 0.5 условия выполняются в полосе 0 < Im(k) < 1. Эти выводы получаются из изучения особых точек функций L+(k),L-(k). Далее – обе функции растут на бесконечности к по модулю не быстрее многочленов первой степени. Наш полином в числителе – это константа, полином нулевой степени, иначе не выполняется условие сходимости произведения L+U+ ,L-U- .Значит
$IMAGE43$,
и, применяя обратное преобразование Фурье, находим u+(x):
$IMAGE44$,
что верно для $IMAGE45$Решение в квадратурах найдено, этот интеграл подлежит простому подсчету. На выходе получим:
$IMAGE46$
Как видим, решение получено с точностью до константы.
1.3 В общем виде
Изложим метод Винера-Хопфа в общем виде. Возьмем обобщенное уравнение
$IMAGE47$
и поставим задачу: найти функции Ψ1, Ψ2,удовлетворяющие нашему уравнению в полосе $IMAGE48$,стремящихся к нулю при $IMAGE49$.A,B,C – аналитические в нашей полосе функции, для ограничения вырожденного случая A,B не равны в полосе нулю. Идею решения такого уравнения мы в основном уже излагали, здесь она немного расширена. Итак, представляем A/B как частное функций L+ ,L- ,
$IMAGE50$,
причем L+ аналитическая в области Im(k) > τ-, L- аналитическая в области Im(k) < τ+ .Подставляя это в уравнение, и приводя к общему знаменателю, получаем:
$IMAGE51$
Теперь, если удается разбить слагаемое, не содержащее Ψ,на два, как
$IMAGE52$,
что будет верно в некоторой подполосе нашей полосы, и сгруппировать идентичные слагаемые, то получаем:
$IMAGE53$
- это чуть более общее равенство, чем то, что мы получали ранее для частного случая. Как и ранее – из сходимости обоих пси к нулю при стремлении k по модулю к бесконечности, сходимости L+ L- не быстрее многочлена степени n, а также учитывая, что существует единственная пси в нашей полосе, составленная из Ψ1, Ψ2, мы получаем следующие соотношения:
$IMAGE54$
Рn(k) – многочлен, коэффициенты которого определяются из доп.условий. Далее – решение будет равно обратному преобразованию Фурье от суммы Ψ1, Ψ2.
Что осталось выяснить, так это саму возможность так раскладывать функции. Приведем нескольку лемм, обосновывающих возможность такой работы с нашими функциями.
Лемма1: Пусть образ F(k) аналитический в полосе $IMAGE55$,F(k) равномерно стремится к 0 при |k|-> ∞ Тогда в этой полосе возможно разбиение функции F как $IMAGE56$,F+(k) аналитическая в Im(k)>τ- , F-(k) аналитическая в Im(k)<τ+ .
$IMAGE57$
Доказательство: Рассмотрим систему отсчета так, как это изображено на картинке. Посчитаем значение F(k0) – в точке, лежащей внутри прямоугольного контура abcd.По формуле Коши расписали в интеграл по контуру.Перейдем к пределу A ->∞,и устремим контур к полосе.
$IMAGE58$
Тогда в пределе получаем
$IMAGE59$,
где эти части есть
$IMAGE60$
Каждая функция задана в своей области, а на их пересечении в нашей полосе мы имеем равенство. Что и требовалось доказать, в общем то. Очевидно, что из их сходимости следует и ограниченность F+(k),F-(k) в рассматриваемой полосе.
Лемма2:Пусть функция Ф(k) является аналитической и не равной нулю в полосе $IMAGE61$,причем Ф(k) равномерно стремится к 1 при |k|->∞.Тогда $IMAGE62$,где функции Ф+,Ф- соответственно аналитические в
$IMAGE63$ и $IMAGE64$
Доказательство:
Заметим, что для функции $IMAGE65$выполнены условия леммы1,значит,мы имеем право ее представить суммой F+ , F- , а Ф – произведением:
$IMAGE66$,Ф=Ф+*Ф- .
Условия на границы по мнимой оси для функций Ф+,Ф- сохранятся => лемма доказана.
Теперь сделаем еще одно обобщение – покажем, как в общих чертах работает этот метод для неоднородного уравнения
$IMAGE67$ (7)
Проводя аналогичные рассуждения, разбивая u(x) на две вспомогательные функции, замечаем, что при выполнении условий для модуля
$IMAGE68$
в полосе $IMAGE69$ мы можем переходить к образам функций и мы получим
$IMAGE70$
предварительно разбив F на две. Принимая за функцию L(x) ф-ю
$IMAGE71$,
аналитическую в стандартной полосе $IMAGE72$ и равномерно стремящуюся к 1 при $IMAGE73$наше алгебра