Метод векторів та його застосування
Вступ
Поняття вектора є одним із фундаментальних понять сучасної математики. Його можна визначити по-різному: як напрямлений відрізок, як упорядковану пару точок, що є кінцями напрямленого відрізка, як множину однаково напрямлених відрізків однакової довжини, як упорядковану пару чисел, як паралельне перенесення.
Уперше поняття вектора як напрямленого відрізка знайшло застосування в механіці для зображення фізичних векторних величин: швидкості, прискорення, сили, моменту сили тощо. Високий ступінь наочності і простота геометричних операцій над векторами як напрямленими відрізками сприяли тому, що поняття вектора знайшло загальне визнання і застосування в інших розділах фізики: в кінематиці, статиці, динаміці точки і динаміці системи, в теорії потенціалу та гідродинаміці, а також стало одним із основних понять таких наук, як векторна алгебра, векторний аналіз, теорія поля, тензорний аналіз тощо.
Проте хоча поняття вектора знайшло перше застосування в фізиці, це математичне поняття, усі операції над якими виконуються за законами математики.
Вектор як математичне поняття міцно ввійшов у шкільну математику, у різні нематематичні науки. В школі за допомогою векторного метод розв’язується багато різноманітних задач, які не мають іншого способу розв’язання.
Саме тому вивчення поняття вектора є дуже важливим в сучасних умовах розвитку математичних наук.
1. Поняття вектора
В елементарній геометрії, як відомо, відрізком AB називається сукупність всіх точок прямої, що лежать між A і B. Точки A і B називаються кінцями відрізка. При цьому, очевидно, порядок, в якому беруться кінці відрізка, несуттєвий. Однак при використанні геометрії у вивченні фізики, особливо механіки, часто доводиться розглядати напрямлені відрізки, тобто відрізки, для яких вказані початкова і кінцева точки. Тобто AB і BA геометрично один і той же відрізок, то, розглядаючи їх як напрямлені відрізки, ми повинні враховувати, що вони задають різні об’єкти.
Означення 1. Відрізок АВ називається напрямленим, якщо береться до уваги порядок його кінцевих точок. Перша точка (А) називається його початком, а друга (В) – його кінцем.
Позначають напрямлений відрізок так: АВ.
Означення 2. Довжиною напрямленого відрізка  називається
називається
довжина відрізка АВ. Позначають: 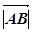 . Звідси
. Звідси 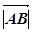 = АВ =
= АВ = 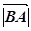
Означення 3. Напрямлені відрізки АВ і CD називаються однаково напрямленими (спів напрямленими), якщо однаково напрямлені промені АВ і CD, і протилежно напрямленими, якщо ці промені протилежно напрямлені.
Означення 4. Вектором називається множина однаково напрямлених (спів напрямлених) відрізків однакової довжини.
Означення 4.1. Вектором називається напрямлений відрізок, тобто відрізок, для якого вказано, яка з обмежуючих його точок рахується першою, яка – другою. Перша точка напрямленого відрізка називається початком вектора, а друга точка – кінцем.
Напрямок вектора на кресленні відмічається стрілкою, оберненою гострим кінцем до кінця вектора. В тексті вектор записується двома великими літерами латинського алфавіту зі спільною рискою зверху, при цьому перша з них позначає початок, друга – кінець вектора. Наприклад,  , $IMAGE6$ (мал. 1.a), причому А, C – відповідно початки, а В, D – кінці даних векторів. В деяких випадках вектор позначається також однією малою літерою, наприклад, a, b, c,… (мал. 1.b).
, $IMAGE6$ (мал. 1.a), причому А, C – відповідно початки, а В, D – кінці даних векторів. В деяких випадках вектор позначається також однією малою літерою, наприклад, a, b, c,… (мал. 1.b).
| | | | | |
| $IMAGE7$ |
| | $IMAGE8$ |
| | | $IMAGE9$ |
|
$IMAGE10$
мал. 1.a мал. 1.b
Означення 5. Вектори  і $IMAGE6$ називаються однаково напрямленими (спів напрямленими), якщо спів напрямлені відповідні їм напрямлені відрізки
і $IMAGE6$ називаються однаково напрямленими (спів напрямленими), якщо спів напрямлені відповідні їм напрямлені відрізки  і $IMAGE6$ (мал. 2.a), і протилежно напрямленими, якщо напрямлені відрізки
і $IMAGE6$ (мал. 2.a), і протилежно напрямленими, якщо напрямлені відрізки  і $IMAGE6$ протилежно напрямлені (мал. 2.b).
і $IMAGE6$ протилежно напрямлені (мал. 2.b).
$IMAGE17$ $IMAGE18$ $IMAGE7$ $IMAGE20$
мал. 2.a мал. 2.b
Означення 6. Довжиною (модулем) вектора називається довжина будь-якого представника класу спів напрямлених відрізків, який визначає цей вектор.
Інакше кажучи, довжиною вектора називається довжина напрямного відрізка, який зображає цей вектор.
Модуль вектора $IMAGE21$ позначають $IMAGE22$, а вектора АB – 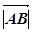 .
.
Вектор, початок якого збігається з його кінцем, називається нульовим вектором, позначають $IMAGE24$ або $IMAGE25$. Нульовий вектор не визначає ніякого напряму, а його довжина вважається рівною нулю.
Вектор, довжина якого дорівнює одиниці, називається одиничним вектором, або ортом.
Рівність векторів
Означення 1. Два вектори називаються рівними, якщо множини відповідних їм напрямлених відрізків збігаються. Пишуть: $IMAGE21$= $IMAGE27$.
Всі нульові вектори вважаться рівними один одному.
Із цього означення випливає така ознака рівності двох векторів.
Теорема 1. (перша ознака рівності двох векторів).
Для того щоб два вектори були рівними, необхідно і достатньо, щоб вони були однаково напрямленими і мали рівні довжини.
Доведення:
1. Необхідність. Нехай вектори  і $IMAGE6$ рівні. Доведемо, що
і $IMAGE6$ рівні. Доведемо, що  $IMAGE31$ $IMAGE6$ і
$IMAGE31$ $IMAGE6$ і 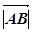 = $IMAGE34$.
= $IMAGE34$.
Якщо  = $IMAGE6$, то, за означенням 1, множини напрямлених відрізків, які відповідають цим векторам, збігаються. Тому
= $IMAGE6$, то, за означенням 1, множини напрямлених відрізків, які відповідають цим векторам, збігаються. Тому  $IMAGE31$ $IMAGE6$,
$IMAGE31$ $IMAGE6$, 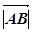 = $IMAGE34$. Звідси
= $IMAGE34$. Звідси  $IMAGE31$ $IMAGE6$,
$IMAGE31$ $IMAGE6$, 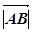 = $IMAGE34$, що й треба було довести.
= $IMAGE34$, що й треба було довести.
2. Достатність. Нехай  $IMAGE31$ $IMAGE6$,
$IMAGE31$ $IMAGE6$, 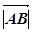 = $IMAGE34$. Доведемо, що
= $IMAGE34$. Доведемо, що  = $IMAGE6$. Якщо,
= $IMAGE6$. Якщо,  $IMAGE31$ $IMAGE6$,
$IMAGE31$ $IMAGE6$, 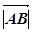 = $IMAGE34$, то $IMAGE59$ $IMAGE31$ $IMAGE61$, $IMAGE62$= $IMAGE63$, тобто
= $IMAGE34$, то $IMAGE59$ $IMAGE31$ $IMAGE61$, $IMAGE62$= $IMAGE63$, тобто  і $IMAGE6$ належать одній і тій же множині однаково напрямлених відрізків рівної довжини. А це означає, що
і $IMAGE6$ належать одній і тій же множині однаково напрямлених відрізків рівної довжини. А це означає, що  = $IMAGE6$. Теорему доведено.
= $IMAGE6$. Теорему доведено.
Наслідок. Два вектори, кожен з яких дорівнює третьому, рівні між собою.
Теорема 2. (теорема про відкладання вектора).
Від будь-якої точки простору можна відкласти вектор, рівний даному, і до того ж єдиний.
Доведення: Нехай даний вектор $IMAGE21$ зображається напрямленим відрізком $IMAGE59$. Виберемо у просторі довільну точку О, сполучимо точку В з точкою О і позначимо середину відрізка ОВ через С (мал. 3). Проведемо
$IMAGE70$
відрізок АС і відкладемо на його продовженні відрізок CM=АС. Чотирикутник АВМО є паралелограмом, бо його діагоналі точкою перетину діляться пополам. Звідси випливає, що промені АВ і ОМ однаково напрямлені, а відрізки АВ і ОМ рівні. Отже, $IMAGE71$=  = $IMAGE21$.
= $IMAGE21$.
$IMAGE74$
Доведемо тепер, що цей вектор єдиний. Припустимо, що існує інший вектор $IMAGE75$= $IMAGE21$, відмінний від $IMAGE71$. Але ж і $IMAGE71$= $IMAGE21$, тому $IMAGE75$= $IMAGE71$. Отже, $IMAGE75$ $IMAGE31$ $IMAGE71$, $IMAGE85$= $IMAGE86$, тому точки M і $IMAGE87$ збігаються, що суперечить припущенню. Тобто від точки O можна відкласти лише один вектор, рівний даному вектору $IMAGE21$. Теорему доведено.
Означення 2. Два вектори називаються протилежними, якщо вони протилежно напрямлені і мають рівні довжини. Вектор, протилежний до $IMAGE21$, позначається - $IMAGE21$ (мал. 4). Очевидно,  =- $IMAGE92$, – (- $IMAGE21$)= $IMAGE21$.
=- $IMAGE92$, – (- $IMAGE21$)= $IMAGE21$.
Додавання векторів, властивості операції додавання векторів
$IMAGE95$
Введемо операцію додавання векторів, яка відіграє важливу роль в векторній алгебрі.
Означення. Нехай задано два вектори $IMAGE21$ і $IMAGE27$. Від деякої точки A відкладемо вектор  = $IMAGE21$, потім від точки B відкладемо вектор $IMAGE100$= $IMAGE27$. Вектор $IMAGE102$= $IMAGE103$ називається сумою векторів $IMAGE21$ і $IMAGE27$ і позначається так: $IMAGE103$= $IMAGE21$+ $IMAGE27$ (мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A, B і C
= $IMAGE21$, потім від точки B відкладемо вектор $IMAGE100$= $IMAGE27$. Вектор $IMAGE102$= $IMAGE103$ називається сумою векторів $IMAGE21$ і $IMAGE27$ і позначається так: $IMAGE103$= $IMAGE21$+ $IMAGE27$ (мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A, B і C  + $IMAGE100$= $IMAGE102$, або: сумою векторів $IMAGE21$ і $IMAGE27$ євектор $IMAGE103$, який сполучає початок вектора $IMAGE21$ з кінцем вектора $IMAGE27$ при умові, що вектор $IMAGE27$ відкладено від кінця вектора $IMAGE21$.
+ $IMAGE100$= $IMAGE102$, або: сумою векторів $IMAGE21$ і $IMAGE27$ євектор $IMAGE103$, який сполучає початок вектора $IMAGE21$ з кінцем вектора $IMAGE27$ при умові, що вектор $IMAGE27$ відкладено від кінця вектора $IMAGE21$.
З цього правила випливає правило паралелограма: якщо вектори $IMAGE21$ і $IMAGE27$ відкладені від спільного початку O, $IMAGE121$= $IMAGE21$, $IMAGE123$= $IMAGE27$ (мал. 6) і на них побудовано паралелограм OACB, то сумою векторів $IMAGE21$+ $IMAGE27$ є вектор $IMAGE103$= $IMAGE128$, який виходить з того ж початку і збігається з діагоналлю OC паралелограма.
Розглянемо властивості операції додавання векторів.
$IMAGE129$
Властивість 1. Операція додавання векторів комутативна, тобто для будь-яких векторів $IMAGE21$ і $IMAGE27$: $IMAGE21$+ $IMAGE27$= $IMAGE27$+ $IMAGE21$.
$IMAGE136$Доведення: За правилом трикутника маємо (мал. 7):
Властивість 2. Операція додавання векторів асоціативна, тобто для будь-яких векторів $IMAGE21$, $IMAGE27$, $IMAGE103$: ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$= $IMAGE21$ +( $IMAGE27$+ $IMAGE103$)
Доведення: Візьмемо довільну точку A і від неї відкладемо вектори  = $IMAGE21$, $IMAGE100$= $IMAGE27$, $IMAGE6$= $IMAGE103$ (мал. 8). Тоді $IMAGE21$+ $IMAGE27$= $IMAGE102$, ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$= $IMAGE158$; $IMAGE27$+ $IMAGE103$= $IMAGE161$; $IMAGE21$+( $IMAGE27$+ $IMAGE103$)= $IMAGE158$. Отже, ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$ = $IMAGE21$+( $IMAGE27$+ $IMAGE103$).
= $IMAGE21$, $IMAGE100$= $IMAGE27$, $IMAGE6$= $IMAGE103$ (мал. 8). Тоді $IMAGE21$+ $IMAGE27$= $IMAGE102$, ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$= $IMAGE158$; $IMAGE27$+ $IMAGE103$= $IMAGE161$; $IMAGE21$+( $IMAGE27$+ $IMAGE103$)= $IMAGE158$. Отже, ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$ = $IMAGE21$+( $IMAGE27$+ $IMAGE103$).
$IMAGE172$
Властивість 3. Сумою протилежних векторів є нуль-вектор: $IMAGE21$+(- $IMAGE21$)=0.
Доведення. Нехай $IMAGE21$=  , тоді - $IMAGE21$= $IMAGE92$, і за правилом трикутника матимемо $IMAGE21$ +(- $IMAGE21$)=
, тоді - $IMAGE21$= $IMAGE92$, і за правилом трикутника матимемо $IMAGE21$ +(- $IMAGE21$)=  + $IMAGE92$= $IMAGE24$=0.
+ $IMAGE92$= $IMAGE24$=0.
Властивість 4. Нуль-вектор є нейтральним елементом операції додавання: $IMAGE21$+ $IMAGE25$= $IMAGE25$+ $IMAGE21$.
$IMAGE188$
Доведення: Нехай $IMAGE21$=  , $IMAGE25$= $IMAGE192$, тоді за правилом трикутника $IMAGE21$+ $IMAGE25$=
, $IMAGE25$= $IMAGE192$, тоді за правилом трикутника $IMAGE21$+ $IMAGE25$=  + $IMAGE192$=
+ $IMAGE192$=  = $IMAGE21$.
= $IMAGE21$.
З наведених властивостей додавання векторів випливає, що операція додавання векторів має ті ж властивості, що й операція додавання чисел. Тому часто при перетворенні сум векторів діємо так само, як і при перетворенні числових виразів: ( $IMAGE21$+ $IMAGE27$)+ $IMAGE103$= $IMAGE21$+( $IMAGE27$+ $IMAGE103$)=( $IMAGE27$+ $IMAGE103$)+ $IMAGE21$= $IMAGE27$( $IMAGE103$+ $IMAGE21$).
Сума більшої кількості векторів знаходиться за правилом многокутника. Щоб знайти суму n векторів $IMAGE211$ (мал. 9), потрібно з довільної точки O відкласти вектор $IMAGE121$= $IMAGE213$, з його кінця – вектор $IMAGE214$= $IMAGE215$,…, $IMAGE216$= $IMAGE217$ (початок кожного наступного вектора-доданка є кінцем попереднього). Вектор $IMAGE103$= $IMAGE219$ буде сумою даних векторів.
Віднімання векторів
Операція віднімання векторів вводиться як протилежна до додавання. Означення. Різницею векторів $IMAGE21$