ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Определение. Вектором называется направленный отрезок прямой. Точка 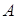 называется началом вектора 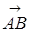, а точка  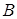– его концом (рис. 1).

Обозначения: , .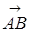

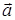$IMAGE6$

Определение. Длина вектора называется его модулем и обозначается $IMAGE7$,    $IMAGE8$.

Определение. Координатами вектора 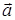 называются координаты его конечной точки. На плоскости Oxy $IMAGE10$; в пространстве Oxyz $IMAGE11$.

Определение. Суммой и разностью векторов $IMAGE12$ и $IMAGE13$ являются соответственно векторы

$IMAGE14$;

$IMAGE15$;

произведение вектора 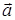 на число l есть вектор

$IMAGE17$.

Определение. Длина вектора равна корню квадратному из суммы квадратов его координат:

$IMAGE18$ (на плоскости);

$IMAGE19$ (в пространстве).

Определение. Расстояние d между двумя точками A и B можно рассматривать как длину вектора $IMAGE20$, т.е.

$IMAGE21$ (на плоскости);

$IMAGE22$ (в пространстве).

Определение. Если два вектора $IMAGE23$ и $IMAGE24$перпендикулярны, то

$IMAGE25$ (на плоскости);

$IMAGE26$ (в пространстве).

Определение Вектор X называется собственным вектором линейного оператора A (матрицы A), если найдется такое число l, что AX=lX.

Число l называется собственным значением оператора A, заданного  матрицей A, т.е. собственные значения находятся из характеристического уравнения $IMAGE27$.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Определение Обыкновенное дифференциальное уравнение – уравнение, связывающее искомую функцию одной переменной и производные различных порядков данной функции.

Определение Порядок старшей производной – порядок дифференциального уравнения.

Определение Решение дифференциального уравнения – такая функция y=y(x), которая при подстановке ее в это уравнение обращает его в тождество.

Определение Задача нахождения решения дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения.

Определение Общее решение дифференциального уравнения n- го порядка называется такое его решение $IMAGE28$, которое является функцией переменной x и n постоянных. Частное решение при конкретных значениях $IMAGE29$.

Определение Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде

$IMAGE30$.

Определение Д.у. первого порядка называется однородным, если оно может быть представлено в виде

$IMAGE31$.

(Для решения используется замена t=y/x)/

Определение Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид

$IMAGE32$ (линейное неоднородное).

(Сначала решаем уравнение $IMAGE33$ - линейное однородное, находим y и подставляем в исходное).

Определение Уравнение вида

$IMAGE34$

называется уравнением Бернулли.

(Для решения используется замена $IMAGE35$).

Линейные однородное д.у. второго порядка с постоянными коэффициентами

Определение Линейные однородные д.у. второго порядка с постоянными коэффициентами имеет вид

$IMAGE36$=0

(Для решения этого уравнения составляем характеристическое уравнение $IMAGE37$).

Теорема 1) Пусть характеристическое уравнение имеет действительные корни l₁ и l₂, причем $IMAGE38$. Тогда общее решение уравнения имеет вид

$IMAGE39$ (С₁, С₂ – некоторые числа).

2) Если характеристическое уравнение имеет один корень l (кратности 2),то общее решение имеет вид

$IMAGE40$ (С₁, С₂ – некоторые числа).

3) Если характеристическое уравнение не имеет действительных корней, то общее решение имеет вид

$IMAGE41$, где

$IMAGE42$, С₁, С₂ – некоторые числа.

НЕОБХОДИМЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ О КАСАТЕЛЬНОЙ

Общее уравнение прямой:

Ax+By+C=0

Уравнение прямой с угловым коэффициентом:

y=kx+b

(k=tgj коэффициент прямой равен тангенсу угла наклона этой прямой)

Если две прямые y=k₁x+b₁ и y=k₂+b₂ параллельны, то k₁=k₂.

Если две прямые y=k₁x+b₁ и y=k₂+b₂ перпендикулярны, то k₁*k₂=-1.

Уравнение прямой, проходящей через данную точку в данном направлении(известен коэффициент k):

Пусть прямая проходит через точку M₁(x₁;y₁) и образует с осью Ox угол $IMAGE43$

y-y₁=k(x-x₁)

Уравнение прямой, проходящей через две данные точки M₁(x₁;y₁) и M₂(x₂;y₂):

$IMAGE44$

Уравнение касательной к кривой y=f(x) в точке x₀ примет вид

y-f(x₀)=f¢(x₀)(x-x₀)

Геометрический смысл производной:

f¢(x₀)=k=tga

(производная f¢(x₀) есть угловой коэффициент(тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке x₀)

МАТРИЦЫ

Определение: Матрицей размера m $IMAGE45$n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрица размера m $IMAGE45$n:

$IMAGE47$.

Виды матриц

Определение: Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца – матрицей (вектором)- столбцом.

Пример:

$IMAGE48$;           $IMAGE49$.

Определение: Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Пример:

$IMAGE50$- квадратная матрица третьего порядка.

Определение: Элементы матрицы a_ij, у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы.

Определение: Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Пример:

$IMAGE51$- диагональная матрица третьего порядка.

Определение: Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой E.

Пример:

$IMAGE52$ - единичная матрица второго порядка;

$IMAGE53$- единичная матрица третьего порядка.

Определение: Матрица любого размера называется нулевой, если все элементы равны нулю.

Операции над матрицами

1. Умножение матрицы на число

Каждый элемент матрицы умножается на это число.

Пример:

$IMAGE54$,  0,5 $IMAGE55$.

2. Сложение матриц

!!! Можно складывать матрицы только одинаковых размеров.

Матрицы складываются поэлементно.

Пример:

$IMAGE56$.

3. Вычитание матриц

!!! Можно вычитать матрицы только одинаковых размеров.

Матрицы вычитаются поэлементно.

Пример:

$IMAGE57$.

4. Умножение матриц

!!! Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В.

Произведением матрицы $IMAGE58$ называется такая матрица $IMAGE59$, каждый элемент которой c_ij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.

5. Возведение в степень

Целой положительной степенью А^m (m>1) квадратной матрицы А называется произведение m матриц равных А, т.е.

$IMAGE60$.

Пример:

$IMAGE61$, найти А².

$IMAGE62$

6. Транспонирование матрицы

Транспонированная матрица – матрица, в которой строки и столбцы поменялись местами с сохранением порядка. Обозначается $IMAGE63$.

Пример:

$IMAGE64$.

Обратная матрица

Определение: Матрица $IMAGE65$называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е.

$IMAGE66$.

!!! Обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная (т.е. определитель матрицы отличен от нуля).

Алгоритм вычисления обратной матрицы:

1. Находим определитель матрицы, т.е. $IMAGE67$.

2. Находим транспонированную матрицу , т.е. $IMAGE63$.

3. Находим присоединенную матрицу, т.е $IMAGE69$ (матрица, состоящая из алгебраических дополнений к элементам транспонированной матрицы).

4. Вычисляем обратную матрицу по формуле $IMAGE70$.

5. Проверяем правильность вычисления, исходя из определения обратной матрицы.

Ранг матрицы

Определение: Ранг матрицы – это наивысший порядок, отличных от 0, миноров матрицы.

!!! Чтобы найти ранг матрицы нужно сначала привести матрицу с помощью элементарных преобразований к ступенчатому виду (все элементы, стоящие ниже главной диагонали, равны 0).

Элементарными называются следующие преобразования матриц:

1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля;

2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

3) перемена местами строк (столбцов) матрицы;

4) отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

На практике часто сталкиваемся с задачей о сглаживании экспериментальных зависимостей.

Пусть зависимость между двумя переменными x и y выражается в виде таблицы, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистической обработки материала и т.п.