Курс лекций по дисциплине
«Матричный анализ»
для студентов II курса
математического факультета специальности
«Экономическая кибернетика»
(лектор Дмитрук Мария Александровна)
Глава 3. Функции от матриц.
1. Определение функции.
Df. Пусть 
– функция скалярного аргумента. Требуется определить, что понимать под f(A), т.е. нужно распространить функцию f(x) на матричное значение аргумента.
Решение этой задачи известно, когда f(x) – многочлен: 
, тогда 
.
Определение f(A) в общем случае.
Пусть m(x) – минимальный многочлен А и он имеет такое каноническое разложение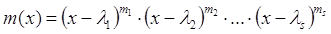 
, $IMAGE6$, $IMAGE7$– собственные значения А. Пусть многочлены g(x) и h(x) принимают одинаковые значения.
Пусть g(A)=h(A) (1), тогда многочлен d(x)=g(x)-h(x) – аннулирующий многочлен для А, так как d(A)=0, следовательно, d(x) делится на линейный многочлен, т.е. d(x)=m(x)*q(x) (2).
Тогда $IMAGE8$, т.е. $IMAGE9$(3), $IMAGE10$, $IMAGE11$, $IMAGE12$.
Условимся m чисел для f(x) таких $IMAGE13$ называть значениями функции f(x) на спектре матрицы А, а множество этих значений будем обозначать $IMAGE14$.
Если множество f(Sp A) определено для f(x), то функция определена на спектре матрицы А.
Из (3) следует, что многочлены h(x) и g(x) имеют одинаковые значения на спектре матрицы А.
Наши рассуждения обратимы, т.е. из (3) Þ (3) Þ (1). Таким образом, если задана матрица А, то значение многочлена f(x) вполне определяется значениями этого многочлена на спектре матрицы А, т.е. все многочлены gi(x), принимающие одинаковые значения на спектре матрицы имеют одинаковые матричные значения gi(A). Потребуем, чтобы определение значения f(A) в общем случае подчинялось такому же принципу.
Значения функции f(x) на спектре матрицы А должны полносильно определить f(A), т.е. функции, имеющие одни и те же значения на спектре должны иметь одно и то же матричное значение f(A). Очевидно, что для определения f(A) в общем случае, достаточно найти многочлен g(x), который бы принимал те же значения на спектре А, что и функция f(A)=g(A).
Df. Если f(x) определена на спектре матрицы А, то f(A)=g(A), где g(A) – многочлен, принимающий на спектре те же значения, что и f(A), $IMAGE15$
Df. Значением функции от матрицы А назовем значение многочлена от этой матрицы при $IMAGE15$.
Среди многочленов из С[x], принимающих одинаковые значения на спектре матрицы А, что и f(x), степени не выше (m-1), принимающий одинаковые значения на спектре А, что и f(x) – это остаток от деления любого многочлена g(x), имеющего те же значения на спектре матрицы А, что и f(x), на минимальный многочлен m(x)=g(x)=m(x)*g(x)+r(x).
Этот многочлен r(x) называют интерполяционным многочленом Лагранжа-Сильвестра для функции f(x) на спектре матрицы А.
Замечание. Если минимальный многочлен m(x) матрицы А не имеет кратных корней, т.е. $IMAGE17$, то значение функции на спектре $IMAGE18$.
Пример:
Найти r(x) для произвольной f(x), если матрица
$IMAGE19$. Построим f(H1). Найдем минимальный многочлен H1 – последний инвариантный множитель [xE-H1]:
$IMAGE20$, dn-1=x2; dn-1=1;
mx=fn(x)=dn(x)/dn-1(x)=xnÞ 0 – n –кратный корень m(x), т.е. n-кратные собственные значения H1.
$IMAGE21$, r(0)=f(0), r’(0)=f’(0),…,r(n-1)(0)=f(n-1)(0) Þ $IMAGE22$.
2. Свойства функций от матриц.
Свойство № 1. Если матрица $IMAGE23$имеет собственные значения $IMAGE24$ (среди них могут быть и кратные), а $IMAGE25$, то собственными значениями матрицы f(A) являются собственные значения многочлена f(x): $IMAGE26$.
Доказательство:
Пусть характеристический многочлен матрицы А имеет вид:
$IMAGE27$, $IMAGE25$, $IMAGE29$. Посчитаем $IMAGE30$. Перейдем от равенства к определителям: $IMAGE31$ $IMAGE32$
Сделаем замену в равенстве:
$IMAGE33$ (*)
Равенство (*) справедливо для любого множества f(x), поэтому заменим многочлен f(x) на $IMAGE34$, получим:
$IMAGE35$.
Слева мы получили характеристический многочлен для матрицы f(A), разложенный справа на линейные множители, откуда следует, что $IMAGE26$ – собственные значения матрицы f(A).
ЧТД.
Свойство № 2. Пусть матрица $IMAGE23$и $IMAGE24$ – собственные значения матрицы А, f(x) – произвольная функция, определенная на спектре матрицы А, тогда собственные значения матрицы f(A) равны $IMAGE39$.
Доказательство:
Т.к. функция f(x) определена на спектре матрицы А, то существует интерполяционный многочлен матрицы r(x) такой, что $IMAGE40$, а тогда f(A)=r(A), а у матрицы r(A) собственными значениями по свойству № 1 будут $IMAGE41$ которым соответственно равны $IMAGE39$.
ЧТД.
Свойство № 3. Если А и В подобные матрицы, $IMAGE43$, т.е. $IMAGE44$, и f(x) – произвольная функция, определенная на спектре матрицы А, тогда $IMAGE45$
Доказательство:
Т.к. А и В подобны, то их характеристические многочлены одинаковы Þ одинаковы и их собственные значения, поэтому значение f(x) на спектре матрицы А совпадает со значение функции f(x) на спектре матрицы В, при чем существует интерполяционный многочлен r(x) такой, что f(A)=r(A), $IMAGE40$, $IMAGE47$ Þ $IMAGE45$.
ЧТД.
Свойство № 4. Если А – блочно-диагональная матрица $IMAGE49$, то $IMAGE50$
Следствие: Если $IMAGE51$, то $IMAGE52$, где f(x) – функция, определенная на спектре матрицы А.
4. Интерполяционный многочлен Лагранжа-Сильвестра.
Случай № 1.
Пусть дана $IMAGE23$. Рассмотрим первый случай: характеристический многочлен $IMAGE54$ имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е. $IMAGE55$, Sp A – простой. В этом случае построим базисные многочлены lk(x):
$IMAGE56$.
Пусть f(x) – функция, определенная на спектре матрицы А и значениями этой функции на спектре будут $IMAGE26$. Надо построить $IMAGE58$.
Построим:
$IMAGE59$.
Обратим внимание, что $IMAGE60$.
$IMAGE31$ $IMAGE62$
Пример: Построить интерполяционный многочлен Лагранжа-Сильвестра для матрицы $IMAGE63$.
$IMAGE64$Построим базисные многочлены:
$IMAGE65$
$IMAGE66$
$IMAGE67$
Тогда для функции f(x), определенной на спектре матрицы А, мы получим:
$IMAGE68$.
Возьмем $IMAGE69$, тогда интерполяционный многочлен
$IMAGE70$.
Случай № 2.
Характеристический многочлен матрицы А имеет кратные корни, но минимальный многочлен этой матрицы является делителем характеристического многочлена и имеет только простые корни, т.е. $IMAGE17$. В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.
Случай № 3.
Рассмотрим общий случай. Пусть минимальный многочлен имеет вид:
$IMAGE72$,
где m1+m2+…+ms=m, deg r(x)<m.
Составим дробно-рациональную функцию:
$IMAGE73$ и разложим ее на простейшие дроби.
$IMAGE74$
Обозначим: $IMAGE75$. Умножим (*) на $IMAGE76$ и получим
$IMAGE77$
где $IMAGE78$– некоторая функция, не обращающаяся в бесконечность при $IMAGE79$.
Если в (**) положить $IMAGE79$, получим:
$IMAGE81$
$IMAGE82$
Для того, чтобы найти ak3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент aki определяется однозначно.
После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.
$IMAGE83$.
Пример: Найти f(A), если $IMAGE84$, где t – некоторый параметр,
$IMAGE85$.
Найдем минимальный многочлен матрицы А:
$IMAGE86$
$IMAGE87$
$IMAGE88$.
Проверим, определена ли функция на спектре матрицы А
$IMAGE31$ $IMAGE90$
$IMAGE91$
Умножим (*) на (х-3)
$IMAGE92$
при х=3
$IMAGE93$Þ $IMAGE94$
Умножим (*) на (х-5)
$IMAGE95$
$IMAGE96$.
Таким образом, $IMAGE97$ - интерполяционный многочлен.
$IMAGE98$
Пример 2.
Если $IMAGE99$, то доказать, что $IMAGE100$
Найдем минимальный многочлен матрицы А:
$IMAGE101$- характеристический многочлен.
$IMAGE102$
$IMAGE103$
$IMAGE104$
d2(x)=1, тогда минимальный многочлен
$IMAGE105$
$IMAGE106$.
Рассмотрим f(x)=sin x на спектре матрицы:
$IMAGE107$Þ функция является определенной на спектре.
Умножим (*) на $IMAGE108$
$IMAGE109$Þ $IMAGE110$.
Умножим (*) на $IMAGE111$:
$IMAGE112$
$IMAGE113$.
Вычислим g, взяв производную (**):
$IMAGE114$. Полагая $IMAGE115$,
$IMAGE116$, т.е. $IMAGE117$.
Итак, $IMAGE118$,
$IMAGE119$,
$IMAGE120$,
$IMAGE121$.
ЧТД.
Пример 3.
Пусть f(x) определена на спектре матрицы, минимальный многочлен которой имеет вид $IMAGE122$. Найти интерполяционный многочлен r(x) для функции f(x).
Решение: По условию f(x) определена на спектре матрицы А Þ f(1), f’(1), f(2), f ‘(2), f ‘’ (2) определены.
$IMAGE123$.
$IMAGE124$
$IMAGE125$
$IMAGE126$.
Используем метод неопределенных коэффициентов:
$IMAGE127$
$IMAGE128$
$IMAGE129$
$IMAGE130$
Если f(x)=ln x
f(1)=0 f’(1)=1
f(2)=ln 2 f’(2)=0.5 f’’(2)=-0.25
4. Простые матрицы.
Пусть матрица $IMAGE131$, так как С алгебраически замкнутое поле, то характеристический многочлен $IMAGE132$, где $IMAGE133$, ki – алгебраическая кратность корня $IMAGE7$.
Обозначим множество векторов удовлетворяющих собственному значению $IMAGE7$ $IMAGE136$- подпространство, $IMAGE137$, где r – ранг матрицы $IMAGE138$.
Теорема. Если квадратная матрица А имеет собственное значение $IMAGE7$, а матрица $IMAGE138$ имеет $IMAGE141$, то $IMAGE7$ имеет кратность $IMAGE143$.
DF. Размерность $IMAGE144$ называется геометрической кратностью собственного значения $IMAGE7$.
В свете этого определения теорема переформулируется следующим образом:
Теорема. Алгебраическая кратность собственного значения не меньше его геометрической кратности.
DF. Матрица $IMAGE131$ называется простой, если аглебраическая кратность каждого ее собственного значения совпадает с его геометрической кратностью.
Из линейной алгебры следует, что матрица $IMAGE131$ простая тогда и только тогда, когда $IMAGE148$.
Если матрица А простая, тогда существует n линейно независимых собственных векторов x1, x2, …,xn таких, что $IMAGE149$, для $IMAGE150$. Запишем это равенство в матричном виде:
$IMAGE151$
$IMAGE152$, т.е. А – простая тогда и только тогда, когда $IMAGE153$ и $IMAGE154$.
Замечание. Обратим внимание на то, что собственные значения А и А’ совпадают. Действительно, собственные значения для А’ это значения $IMAGE155$. Таким образом характеристические многочлены матриц совпадают. Размерность $IMAGE156$, тогда $IMAGE157$. Поэтому, если $IMAGE7$ - собственное значение матрицы А, то и $IMAGE7$ является собственным значением матрицы А’, т.е. существует $IMAGE160$, что $IMAGE161$ (*) или $IMAGE162$. Транспонируем (*) и получим $IMAGE163$ (транспонируем это равенство). В этом случае $IMAGE164$называют левым собственным вектором матрицы А. Соответственно, $IMAGE165$ - называют правым собственным подпространством, $IMAGE166$- называют левым собственным подп