Вступ
Обрана мною тема курсової роботи – математичні більярди – є дуже цікавою і актуальною. В умовах розвитку комп’ютерних технологій, створень математичних пакетів для вирішення багатьох задач з різних галузей математики постає проблема пошуку найбільш оптимальних шляхів розв’язання. Не останню роль в вирішенні цієї проблеми грає вивчення теорії математичних більярдів. Тому розгляд цього питання, встановлення зв’язків основ цієї теорії з рішеннями проблем інформатики, фізики є достатньо важливим компонентом навчального курсу «Вища математика». Крім цього, деякі відомості доречно було б вивчати в середній школі для розв’язання задач підвищеної складності, при підготовці учнів до математичних олімпіад, на факультативах з математики та в класах з поглибленим вивченням математики.
Вивчення математичних більярдів, як системи руху абсолютно пружного тіла (без врахування опору середовища), послужило основою концепції детермінованого хаосу. До систем, відповідаючім більярдам, зводяться ряд задач статистичної фізики. Багато складних для аналітичного розв’язання математичних задач легко розв’язуються за допомогою побудови траєкторій більярдів в прямокутній та опуклій області. Чітко простежується зв’язок такої науки, як оптики з проблемами побудови траєкторій математичних більярдів в еліпсі та ін.
Все це свідчить про необхідність подальшого розгляду цієї теми, використання для вирішення питань теорії більярдів сучасних комп’ютерних програм. Тому метою моєї роботи було вивчення основних теоретичних відомостей вищезазначеної теми, аналіз можливостей застосування законів теорії в середніх навчальних закладах та використання комп’ютерних програм для оптимізації роботи з пошуку рішення проблемних питань, для наочної демонстрації правил побудови більярдних траєкторій та розширення сфери застосування теорії математичних більярдів. Для цього були вивчені роботи відомих математиків, що займались цією проблемою, проведена спільна з викладачами вищої математики та інформатики ХНПУ ім. Г.С. Сковороди дослідницька робота. В результаті проведеної роботи були отримані наступні висновки, що представлені в двох розділах даної курсової роботи.
Відомості з теорії математичних більярдів
Об’єкт та історія вивчення теорії
Назва більярд походить від французького «billiard» - крива палка або «billart» (кий) та «bille» (куля).
Подібно до того, як азартна гра у кості викликала до життя «обчислення» вірогідності, гра в більярд стала предметом серйозних наукових досліджень з механіки та математики. Опису руху більярдної кулі присвячена книга видатного французького фізика Г.Г. Коріоліса, створена ним в 1835 році. Окремі відомості цієї праці будуть наведені в подальших розділах даної курсової роботи.
Відомі різні варіанти гри на більярді. Наприклад, так званий французькій більярд взагалі не має луз. При грі в цей більярд треба попасти в задану кулю після декількох зіткнень з іншими кулями. Французький більярд і став прообразом математичного більярда.
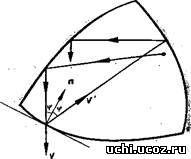
Об’єктом вивчення в математичних більярдах є траєкторія, тобто слід рухомої більярдної одиниці. В загальному випадку ця ламана, що вписана в область Q і складена з нескінченної кількості ланок, на яких вказано напрям руху. Ця ламана може бути однозначно побудована по будь-якій своїй ланці. В окремому випадку, коли більярдна частка вертається в вихідне положення (і після цього знов розпочинає свій рух), ламана замкнена і складається з скінченої кількості ланок. Така траєкторія називається періодичною. Основна ціль теорії математичних більярдів – опис всіляких типів траєкторій в різних областях.
Більярди призводять до багатьох цікавих і красивих математичних задач. О декількох з них розповідається в другій частині даної роботи.
Ці задачі бувають далеко не простими і приховують в собі багато невирішених проблем. Наприклад, досі невідомо, чи в будь-якій області існує періодична більярдна траєкторія (це невідомо навіть для многокутників). Іще один приклад пов'язаний з проблемою висвітлення довільної області з дзеркальними стінками точковим джерелом світла: з деякої точки q € Q випустимо різноманітні промені світла, що дзеркально відбиваються від границі ∂Q; чи освітлять вони (після можливих відбиттів) всю область Q? Відповідь невідома, якщо Q – многокутник. Для плоских областей загального вигляду відповідь негативна.
Окрім використання в чисто математичних задачах, більярди цікаві тим, що моделюють досі складні фізичні процеси. Традиційно більярди використовуються в оптиці (дзеркальне відбиття, задачі про освітлення, фокусіровка променів в лазері) та акустиці (побудова «шепочущіх галерей»), оскільки променям світла та звуковими хвилям притаманні пружні (дзеркальні) відбиття від непроникних поверхонь.
До більярдів можуть бути зведені деякі важливі моделі класичної механіки і гідродинаміки – гази і рідини, що складені з молекул, пружно стикаються один з одним та з стінками ємкості (системи твердих куль). Тут закон пружного зіткнення покладено в самій моделі, зостається лише уявити (закодувати) рух багатьох молекул траєкторією однієї більярдної частки. Багато проблем класичної механіки твердих куль можуть бути сформульовані і вирішені в термінах більярдів. Наприклад, так було розв’язане питання про можливу кількість зіткнень в системі з нескінченної кількості твердих куль у відкритому просторі (без стінок).
Більярдні траєкторії виникають при знаходженні власних функцій оператора Лапласа всередині випуклої області з граничними умовами.
Нескінченно можна перераховувати можливості застосування теорії математичних більярдів. Останнім часом статистична механіка дала великого імпульсу розвитку теорії більярдів. Тому надалі приділимо їй найбільшу увагу.
Проблема чіткого обґрунтування законів статистичної механіки здавна хвилювала розум вчених (в повному обсязі вона не вирішена й досі). Мова йде про вивід законів еволюції систем великої кількості часток (компонент) з рівнянь руху кожної окремої частки (компоненти) під впливом всіх інших часток. Ще в позаминулому сторіччі Л. Больцман вказав, що визначені математичні властивості системи твердих куль можуть бути корисними для такого висновку. Властивості ці – ергодичність, перемішування та інші – не такі прості. Ці властивості (їх називають стохастичним) виявляються також корисними при вивченні багатьох інших явищ, наприклад квантового хаосу.
Ергодичні властивості більярдів обговорювалися ще в працях А. Пуанкаре, Г. Біркгофа і Ж. Адамара. Великий внесок в розуміння ролі цих властивостей для проблем статистичної механіки вніс радянський фізик Н. С. Крилов. Математичний апарат для вивчення ергодичних властивостей більярдів з’явилися в 70-х роках, після того, як в серії праць Д.В. Аносова, Я.Г. Сіная, С. Смейла та інших було створено новий напрямок теорії динамічних систем, що отримало назву теорії гіперболічних динамічних систем. Перше фундаментальне дослідження ергодичних властивостей більярдів належить Я.Г. Сінаю. Його праця відкрила двері для проникнення динамічних систем (хаосу, безповоротності руху, дифузії, релаксації, рівноваги) в математичну теорію більярдів.
В умовах сучасності теорія більярдів здобула відомість і отримала широке визнання в науковому світі. Стали звичними такі поняття, як «стохастичний більярд», «квантовий більярд» «ентропія більярду», «статистичні властивості більярду». В той же час, це порівняно молода теорія. Тому можливості використання новітніх технологій розв’язання можливо допоможуть знайти відповідь на ще нерозв’язані задачі даної теорії.
Перейдемо до загальної математичної проблеми більярду. Вона полягає в тому, щоб змалювати різноманітні типи більярдних траєкторій в даній області Q. Найпростіший принцип такого змалювання – розділ траєкторій на періодичні, або замкнені, і інші – неперіодичні. На малюнку зображені деякі періодичні траєкторій більярдів в прямокутнику, в правильному трикутнику, в колі.
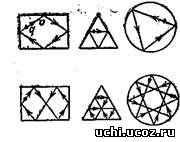
Траєкторія з «початковою умовою» (напрямок, початкове положення точки) буде періодичною, якщо через деякий час (через період) точка повертається в своє першочергове положення з первинною швидкістю. Періодичний рух сприймається як найбільш «правильний». Проблема періодичних траєкторій зводиться до існування: чи в будь-якій області існують замкнені траєкторії?
Іще одне питання – про критерії періодичності: як по даним умовам визначити, чи є задана теорія періодичною?
Цікавість представляють такі питання:
ü Яку кількість ланок може мати періодична траєкторія?
ü Які періоди мають періодичні траєкторії в даній області? (ці питання мають пряме відношення до дослідження спеціальних систем квантової механіки). Перейдемо до розглядання цих питань в простіших поверхневих областях (коло, еліпс, прямокутник, трикутники).
Більярди в опуклих гладких областях
Більярд в колі
Більярд в крузі. Найпростіша область з криволінійною гладкою межею на площині — це, звичайно ж, круг. Правильна, симетрична форма круга приводить до правильного руху більярдної частки: при віддзеркаленнях від межі круга кут падіння залишається постійним!
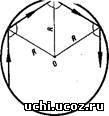
Мал. 1
Якщо цей кут ще і раціональний (в градусах, наприклад, 45°, 30°, 1° або 2,5°), то точки віддзеркалення лягають у вершини правильного многокутника і рух більярдної частки буде періодичним (тобто вона рано чи пізно повернеться в первинне положення і в точності відтворюватиме свою траєкторію) . Якщо ж кут падіння ірраціональний, то точки віддзеркалення усюди щільно заповнюватимуть коло (тобто на будь-якій маленькій дузі їх буде нескінченно багато) і траєкторія ніколи не повернеться в початкове положення. Цей цікавий і досить елементарний факт витікає з теореми Якобі.
Для нас важливо, що у всіх випадках є величина, яка зберігається при русі частки. Ця величина — кут падіння. Така величина називається інваріантом, а у фізиці — частіше першим інтегралом.
· Рівність всіх траєкторій (з рівності кутів)
· Середини всіх ланок траєкторії віддалені від центра кола на однакову відстань.
Будь-яка більярдна траєкторія в колі ніколи не заходить всередину деякого концентричного кола, границі якого дотикаються всі її ланки, тобто це значить, що більярд в колі не ергодичний.
Більярдна траєкторія в колі не всюди щільна. Вид більярдної траєкторії в колі повністю визначається числом α, а саме
Якщо число α таке, що α/π є раціональним числом (тобто дорівнює деякому дробу m/n з цілими m і n), то більярдна траєкторія періодична
Якщо α/π ірраціональне, то відповідаюча куту α траєкторія неперіодична.
Доведення
Α =m/n*2π , m,n – цілі
Nα = 2πm, при повороті на кут nα кожна точка Г переходить в себе.
P0P1P2P3 (вершини більярдної траєкторії: Pn=P0; Pn+1 = P1 ; Pn+2 = P2…)
Тобто вершини, починаючи з n-ої повторюються. (що і свідчить про періодичність більярдних траєкторій)
Якщо m/n нескоро чувана, то траєкторія складається з n ланок. При m=1 – це буде правильний n-кутник, при m>=2 траєкторія представляє собою правильну самоперетинаючуюся замкнену (зірчасту) ламану! Більярдний шар після n віддзеркалень від борта Г опиняється в початковій точці P0 (зробив m обертів навколо центру О).
Уявімо, що більярдна траєкторія періодична/, тоді α і π такі, що α/π – раціональні, а це протирічить умові, що α/π– ірраціональне. Теорему доведено.
Теорема Якобі. Нехай α – невимірне з π (α/π - ірраціональне), {P0,P1,P2,… }={ Pk} – нескінченна послідовність точок послідовності Pk+1 отримується з попередньої точки Pk поворотом навколо центра на α радіан. Тоді для будь-якої дуги Δ кола Г хоча б одна точка послідовності { Pk} лежить на цій дузі.
Теорема Якобі стверджує, що якщо коло провертати на ірраціональний (в градусах) кут р, то образи кожної точка а, а+р, а+2р ... (в кутових координатах, узятих по модулю 360°) заповнять щільно все коло.
Неперіодичний рух може виявитись «майже періодичним», або квазіперіодичним. Квазіперіодичність означає, що хоч його траєкторія і не замкнена, але через деякий час (через квазіперіод) вона буде близько до попереднього відрізку траєкторії. Характерні квазіперіодичні траєкторії для кола показано на малюнку.
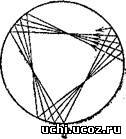
Виявляється, для більярда в колі неперіодична траєкторія має бути квазіперіодичною. Вказані неперіодичні траєкторії всюди щільно заповнюють відповідну область. Якщо вважати, що більярдний шар «чорнильний» і залишає після себе слід, то він з часом обов’язково замалює всю область цілком. Зрозуміло, що періодична траєкторія властивості всюди щільної мати не може – вона може заповнювати область «дуже щільно», але не всюди щільно. Довільна неперіодична траєкторія більярда в колі та еліпсі не є всюди щільною.
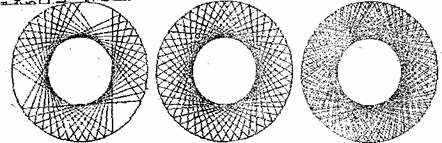
Більярд в кільці. Ще одним прикладом досить правильної області з гладкою криволінійною межою служить кільце, тобто область, укладена між двома концентричними колами. В кільці бувають траєкторії двох типів:
а) що відображаються тільки від зовнішнього круга — ці траєкторії зберігають кут падіння, як і в крузі (вони не «відчувають» присутності внутрішнього круга);
б) що відображаються поперемінно від зовнішнього і від внутрішнього кругів.
$IMAGE6$Траєкторії типу «б» трохи складніше, ніж типу «а», але і у них кути падіння на зовнішнє коло однакові. І на внутрішню — теж, що в