Математический анализ.
Практикум.
Для студентов ВУЗов по специальности:
«Государственное и муниципальное управление»
Т.З. Павлова
Колпашево 2008
Глава 1. Введение в анализ
1.1 Функции. Общие свойства
1.2 Теория пределов
1.3 Непрерывность функции
Глава 2. Дифференциальное исчисление
2.1 Определение производной
2.2 Основные правила дифференцирования
2.3 Производные высших порядков
2.4 Исследование функций
2.4.1 План полного исследования функции
2.4.2 Примеры исследования функции
2.4.3. Наибольшее и наименьшее значение функции на отрезке
2.5 Правило Лопиталя
Глава 3. Интегрально исчисление
3.1 Неопределенный интеграл
3.1.1 Определения и свойства
3.1.2 Таблица интегралов
3.1.3 Основные методы интегрирования
3.2 Определенный интеграл
3.2.1 Понятие определенного интеграла и его свойства
3.2.2 Методы вычисления определенного интеграла
3.2.3 Приложения определенного интеграла
Глава 4. Функции нескольких переменных
4.1 Основные понятия
4.2 Пределы и непрерывность функций нескольких переменных
4.3 Производные и дифференциалы функций нескольких переменных
4.3.1 Частные производные первого порядка
4.3.2 Частные производные второго порядка
4.3.3 Полный дифференциал и его применение к приближенным вычислениям
4.3.4 Дифференцирование неявной функции
Глава 5. Классические методы оптимизации
5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)
Глава 6. Модель потребительского выбора
6.1 Функция полезности.
6.2 Линии безразличия
6.3 Бюджетное множество
6.4 Теория потребительского спроса
Задания для домашней контрольной работы
Литература
Глава 1. Введение в анализ
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной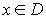 
поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Аналитическое представление функции:
в явном виде: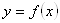 
;
в неявном виде: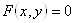 
;
в параметрической форме: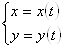 
разными формулами в области определения 
:
$IMAGE6$
Свойства.
Четная функция: $IMAGE7$. Например, функция $IMAGE8$ – четная, т.к. $IMAGE9$.
Нечетная функция: $IMAGE10$. Например, функция $IMAGE11$ – нечетная, т.к. $IMAGE12$.
Периодическая функция: $IMAGE13$, где T – период функции, $IMAGE14$. Например, тригонометрические функции.
Монотонная функция. Если для любых $IMAGE15$ из области определения $IMAGE16$ – функция возрастающая, $IMAGE17$ – убывающая. Например, $IMAGE18$ – возрастающая, а $IMAGE19$– убывающая.
Ограниченная функция. Если существует такое число M, что $IMAGE20$. Например, функции $IMAGE21$ и $IMAGE22$, т.к. $IMAGE23$.
Пример 1. Найти область определения функций.
$IMAGE24$ $IMAGE25$ $IMAGE26$ $IMAGE27$ + 2 – 3 +
$IMAGE28$
Определение 1. Пределом функции $IMAGE29$ при $IMAGE30$ называется число b, если для любого $IMAGE31$ ( $IMAGE31$ – сколь угодно малое положительное число) можно найти такое значение аргумента $IMAGE33$, начиная с которого выполняется неравенство $IMAGE34$.
Обозначение: $IMAGE35$.
Определение 2. Пределом функции $IMAGE29$ при $IMAGE37$ называется число b, если для любого $IMAGE31$ ( $IMAGE31$ - сколь угодно малое положительное число) существует такое положительное число $IMAGE40$, что для всех значений x, удовлетворяющих неравенству $IMAGE41$ выполняется неравенство $IMAGE34$.
Обозначение: $IMAGE43$.
Определение 3. Функция $IMAGE44$ называется бесконечно малой при $IMAGE45$ или $IMAGE30$, если $IMAGE47$или $IMAGE48$.
Свойства.
1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию (постоянную, другую бесконечно малую величину) есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Определение 4. Функция $IMAGE44$ называется бесконечно большой при $IMAGE45$, если $IMAGE51$.
Свойства.
1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Теорема. (Связь между бесконечно малой величиной и бесконечно большой величиной.) Если функция $IMAGE52$ бесконечно малая при $IMAGE45$ ( $IMAGE30$), то функция $IMAGE55$ является бесконечно большой величиной при $IMAGE45$ ( $IMAGE30$). И, обратно, если функция $IMAGE52$ бесконечно большая при $IMAGE45$ ( $IMAGE30$), то функция $IMAGE55$ является бесконечно малой величиной при $IMAGE45$ ( $IMAGE30$).
Теоремы о пределах.
1. Функция не может иметь более одного предела.
2. Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций:
$IMAGE64$.
3. Предел произведения нескольких функций равен произведению пределов этих функций:
$IMAGE65$
4. Предел степени равен степени предела:
$IMAGE66$
5. Предел частного равен частному пределов, если предел делителя существует:
$IMAGE67$.
6. Первый замечательный предел.
$IMAGE68$.
Следствия:
$IMAGE69$
7. Второй замечательный предел:
$IMAGE70$
Следствия:
$IMAGE71$
Эквивалентные бесконечно малые величины при $IMAGE72$:
$IMAGE73$
Вычисление пределов.
При вычислении пределов используют основные теоремы о пределах, свойства непрерывных функций и правила, вытекающие из этих теорем и свойств.
Правило 1. Чтобы найти предел в точке $IMAGE74$ функции, непрерывной в этой точке, надо в функцию, стоящую под знаком предела, вместо аргумента x подставить его предельное значение $IMAGE74$.
Пример 2. Найти
$IMAGE76$
Правило 2. Если при отыскании предела дроби предел знаменателя равен нулю, а предел числителя отличен от нуля, то предел такой функции равен $IMAGE77$.
Пример 3. Найти
$IMAGE78$
Правило 3. Если при отыскании предела дроби предел знаменателя равен $IMAGE79$, а предел числителя отличен от нуля, то предел такой функции равен нулю.
Пример 4. Найти
$IMAGE80$
Часто подстановка предельного значения аргумента приводит к неопределенным выражениям вида
$IMAGE81$.
Нахождение предела функции в этих случаях называется раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразование данного выражения. Для раскрытия неопределенностей используют различные приемы.
Правило 4. Неопределенность вида $IMAGE82$ раскрывается путем преобразования подпредельной функции т.о., чтобы в числителе и знаменателе выделить множитель, предел которого равен нулю, и, сократив на него дробь, найти предел частного. Для этого числитель и знаменатель либо раскладывают на множители, либо домножают на сопряженные числителю и знаменателю выражения.
Пример 5.
$IMAGE83$
Пример 6.
$IMAGE84$
Правило 5. Если подпредельное выражение содержит тригонометрические функции, тогда, чтобы раскрыть неопределенность вида $IMAGE82$ используют первый замечательный предел.
Пример 7.
$IMAGE86$
$IMAGE87$.
Пример 8.
$IMAGE88$
Правило 6. Чтобы раскрыть неопределенность вида $IMAGE89$ при $IMAGE30$, числитель и знаменатель подпредельной дроби необходимо разделить на высшую степень аргумента и находить далее предел частного.
Возможны результаты:
1) искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если эти степени одинаковы;
2) предел равен бесконечности, если степень аргумента числителя выше степени аргумента знаменателя;
3) предел равен нулю, если степень аргумента числителя ниже степени аргумента знаменателя.
Пример 9.
а) $IMAGE91$
т.к. $IMAGE92$
Степени равны, значит, предел равен отношению коэффициентов при старших степенях, т.е. $IMAGE93$.
б) $IMAGE94$
Степень числителя $IMAGE95$, знаменателя – 1, значит, предел равен $IMAGE96$
в) $IMAGE97$
Степень числителя 1, знаменателя – $IMAGE95$, значит, предел равен 0.
Правило 7. Чтобы раскрыть неопределенность вида $IMAGE99$, числитель и знаменатель подпредельной дроби необходимо домножить на сопряженное выражение.
Пример 10.
$IMAGE100$
$IMAGE101$
Правило 8. Чтобы раскрыть неопределенность вида $IMAGE102$ используют второй замечательный предел и его следствия.
Можно доказать, что
$IMAGE103$
Пример 11.
$IMAGE104$
Пример 12.
$IMAGE105$
Пример 13.
$IMAGE106$
Правило 9. При раскрытии неопределенностей, подпредельная функция которых содержит б.м.в., необходимо заменить пределы этих б.м. на пределы б.м., эквивалентных им.
Пример 14.
$IMAGE107$
$IMAGE108$
Пример 15.
$IMAGE109$
$IMAGE110$
Правило 10. Правило Лопиталя (см. 2.6).
Функция 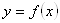непрерывна в точке $IMAGE112$, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
Эквивалентные условия:
1. $IMAGE113$;
2. $IMAGE114$
3. $IMAGE115$
4. $IMAGE116$
Классификация точек разрыва:
разрыв I рода
- устранимый – односторонние пределы существуют и равны;
- неустранимый (скачок) – односторонние пределы не равны;
разрыв II рода: предел функции в точке не существует.
Пример 16. Установить характер разрыва функции 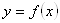в точке $IMAGE118$ или доказать непрерывность функции в этой точке.
а) $IMAGE119$
при $IMAGE118$ функция не определена, следовательно, она не непрерывна в этой точке. Т.к. $IMAGE121$и, соответственно, $IMAGE122$, то $IMAGE118$ – точка устранимого разрыва первого рода.
б) $IMAGE124$
по сравнению с заданием (а) функция доопределена в точке $IMAGE118$ так, что $IMAGE126$, значит, данная функция непрерывна в данной точке.
в) $IMAGE127$
При $IMAGE118$ функция не определена;
$IMAGE129$.
Т.к. один из односторонних пределов бесконечен, то $IMAGE118$ – точка разрыва второго рода.
Глава 2. Дифференциальное исчисление
2.1 Определение производной
Определение производной
Производная $IMAGE131$ или $IMAGE132$ от данной функции 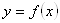есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:
$IMAGE134$ или $IMAGE135$.
Механический смысл производной – скорость изменения функции. Геометрический смысл производной – тангенс угла наклона касательной к графику функции:
$IMAGE136$
| Наименование | Функция | Производная |
| Умножение на постоянный множитель | $IMAGE137$ | $IMAGE138$ |
|