Содержание
Введение
1. Предмет и методы математической статистики
2. Основные понятия математической статистики
2.1 Основные понятия выборочного метода
2.2 Выборочное распределение
2.3 Эмпирическая функция распределения, гистограмма
Заключение
Список литературы
Введение Математическая статистика — наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании).
В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей — свойства и взаимосвязи этих величин (распределений).
Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.
При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину — как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
Все вышеприведенные факторы обуславливают актуальность и значимость тематики работы на современном этапе, направленной на глубокое и всестороннее изучение основных понятий математической статистики.
В связи с этим целью данной работы является систематизация, накопление и закрепление знаний о понятиях математической статистики.
1. Предмет и методы математической статистики Математическая статистика — наука о математических методах анализа данных, полученных при проведении массовых наблюдений (измерений, опытов). В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Существенная часть статистики математической основана на вероятностных моделях. Выделяют общие задачи описания данных, оценивания и проверки гипотез. Рассматривают и более частные задачи, связанные с проведением выборочных обследований, восстановлением зависимостей, построением и использованием классификаций (типологий) и др.
Для описания данных строят таблицы, диаграммы, иные наглядные представления, например, корреляционные поля. Вероятностные модели обычно не применяются. Некоторые методы описания данных опираются на продвинутую теорию и возможности современных компьютеров. К ним относятся, в частности, кластер-анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости, в наименьшей степени исказив расстояния между ними.
Методы оценивания и проверки гипотез опираются на вероятностные модели порождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что изучаемые объекты описываются функциями распределения, зависящими от небольшого числа (1-4) числовых параметров. В непараметрических моделях функции распределения предполагаются произвольными непрерывными. В статистике математической оценивают параметры и характеристики распределения (математическое ожидание, медиану, дисперсию, квантили и др.), плотности и функции распределения, зависимости между переменными (на основе линейных и непараметрических коэффициентов корреляции, а также параметрических или непараметрических оценок функций, выражающих зависимости) и др. Используют точечные и интервальные (дающие границы для истинных значений) оценки.
В математической статистике есть общая теория проверки гипотез и большое число методов, посвященных проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и характеристик, о проверке однородности (то есть о совпадении характеристик или функций распределения в двух выборках), о согласии эмпирической функции распределения с заданной функцией распределения или с параметрическим семейством таких функций, о симметрии распределения и др.
Большое значение имеет раздел математической статистики, связанный с проведением выборочных обследований, со свойствами различных схем организации выборок и построением адекватных методов оценивания и проверки гипотез.
Задачи восстановления зависимостей активно изучаются более 200 лет, с момента разработки К. Гауссом в 1794 г. метода наименьших квадратов. В настоящее время наиболее актуальны методы поиска информативного подмножества переменных и непараметрические методы.
Разработка методов аппроксимации данных и сокращения размерности описания была начата более 100 лет назад, когда К. Пирсон создал метод главных компонент. Позднее были разработаны факторный анализ[1] и многочисленные нелинейные обобщения.
Различные методы построения (кластер-анализ), анализа и использования (дискриминантный анализ) классификаций (типологий) именуют также методами распознавания образов (с учителем и без), автоматической классификации и др.
Математические методы в статистике основаны либо на использовании сумм (на основе Центральной Предельной Теоремы теории вероятностей) или показателей различия (расстояний, метрик), как в статистике объектов нечисловой природы. Строго обоснованы обычно лишь асимптотические результаты. В настоящее время компьютеры играют большую роль в математической статистике. Они используются как для расчетов, так и для имитационного моделирования (в частности, в методах размножения выборок и при изучении пригодности асимптотических результатов).
2. Основные понятия математической статистики Пусть  — случайная величина, наблюдаемая в случайном эксперименте. Предполагается, что вероятностное пространство задано (и не будет нас интересовать).
— случайная величина, наблюдаемая в случайном эксперименте. Предполагается, что вероятностное пространство задано (и не будет нас интересовать).
Будем считать, что, проведя  раз этот эксперимент в одинаковых условиях, мы получили числа
раз этот эксперимент в одинаковых условиях, мы получили числа 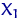 ,
, 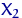 ,
,  , $IMAGE6$— значения этой случайной величины в первом, втором, и т.д. экспериментах. Случайная величина $IMAGE7$имеет некоторое распределение $IMAGE8$, которое нам частично или полностью неизвестно.
, $IMAGE6$— значения этой случайной величины в первом, втором, и т.д. экспериментах. Случайная величина $IMAGE7$имеет некоторое распределение $IMAGE8$, которое нам частично или полностью неизвестно.
Рассмотрим подробнее набор $IMAGE9$, называемый выборкой.
В серии уже произведенных экспериментов выборка — это набор чисел. Но если эту серию экспериментов повторить еще раз, то вместо этого набора мы получим новый набор чисел. Вместо числа $IMAGE10$появится другое число — одно из значений случайной величины $IMAGE11$. То есть $IMAGE10$(и $IMAGE13$, и $IMAGE14$, и т.д.) — переменная величина, которая может принимать те же значения, что и случайная величина $IMAGE11$, и так же часто (с теми же вероятностями). Поэтому до опыта $IMAGE16$— случайная величина, одинаково распределенная с $IMAGE11$, а после опыта — число, которое мы наблюдаем в данном первом эксперименте, т.е. одно из возможных значений случайной величины $IMAGE16$.
Выборка $IMAGE9$объема $IMAGE20$— это набор из $IMAGE20$независимых и одинаково распределенных случайных величин («копий $IMAGE11$»), имеющих, как и $IMAGE11$, распределение $IMAGE8$.
Что значит «по выборке сделать вывод о распределении»? Распределение характеризуется функцией распределения, плотностью или таблицей, набором числовых характеристик — $IMAGE25$, $IMAGE26$, $IMAGE27$и т.д. По выборке нужно уметь строить приближения для всех этих характеристик.
Рассмотрим реализацию выборки на одном элементарном исходе $IMAGE28$— набор чисел $IMAGE29$, $IMAGE30$, $IMAGE31$. На подходящем вероятностном пространстве введем случайную величину $IMAGE32$, принимающую значения 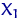 , $IMAGE30$, $IMAGE35$с вероятностями по $IMAGE36$(если какие-то из значений совпали, сложим вероятности соответствующее число раз). Таблица распределения вероятностей и функция распределения случайной величины $IMAGE32$выглядят так:
, $IMAGE30$, $IMAGE35$с вероятностями по $IMAGE36$(если какие-то из значений совпали, сложим вероятности соответствующее число раз). Таблица распределения вероятностей и функция распределения случайной величины $IMAGE32$выглядят так:
| $IMAGE32$ | 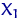 | $IMAGE30$ | $IMAGE35$ | | $IMAGE42$ | $IMAGE36$ | $IMAGE30$ | $IMAGE36$ | | $IMAGE46$ |
Распределение величины $IMAGE32$называют эмпирическим или выборочным распределением. Вычислим математическое ожидание и дисперсию величины $IMAGE32$и введем обозначения для этих величин:
$IMAGE49$
Точно так же вычислим и момент порядка $IMAGE50$
$IMAGE51$
В общем случае обозначим через $IMAGE52$величину
$IMAGE53$
Если при построении всех введенных нами характеристик считать выборку 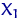 , $IMAGE30$, $IMAGE35$ набором случайных величин, то и сами эти характеристики — $IMAGE57$, $IMAGE58$, $IMAGE59$, $IMAGE60$, $IMAGE61$ — станут величинами случайными. Эти характеристики выборочного распределения используют для оценки (приближения) соответствующих неизвестных характеристик истинного распределения.
, $IMAGE30$, $IMAGE35$ набором случайных величин, то и сами эти характеристики — $IMAGE57$, $IMAGE58$, $IMAGE59$, $IMAGE60$, $IMAGE61$ — станут величинами случайными. Эти характеристики выборочного распределения используют для оценки (приближения) соответствующих неизвестных характеристик истинного распределения.
Причина использования характеристик распределения $IMAGE32$для оценки характеристик истинного распределения $IMAGE7$(или 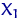 ) — в близости этих распределений при больших
) — в близости этих распределений при больших  .
.
Рассмотрим, для примера, $IMAGE20$подбрасываний правильного кубика. Пусть $IMAGE67$— количество очков, выпавших при $IMAGE68$-м броске, $IMAGE69$. Предположим, что единица в выборке встретится $IMAGE70$раз, двойка — $IMAGE71$раз и т.д. Тогда случайная величина $IMAGE72$будет принимать значения 1, $IMAGE30$, 6 с вероятностями $IMAGE74$,  , $IMAGE76$ соответственно. Но эти пропорции с ростом $IMAGE20$приближаются к $IMAGE78$согласно закону больших чисел. То есть распределение величины $IMAGE72$в некотором смысле сближается с истинным распределением числа очков, выпадающих при подбрасывании правильного кубика.
, $IMAGE76$ соответственно. Но эти пропорции с ростом $IMAGE20$приближаются к $IMAGE78$согласно закону больших чисел. То есть распределение величины $IMAGE72$в некотором смысле сближается с истинным распределением числа очков, выпадающих при подбрасывании правильного кубика.
Мы не станем уточнять, что имеется в виду под близостью выборочного и истинного распределений. В следующих параграфах мы подробнее познакомимся с каждой из введенных выше характеристик и исследуем ее свойства, в том числе ее поведение с ростом объема выборки.
Поскольку неизвестное распределение $IMAGE80$можно описать, например, его функцией распределения $IMAGE81$, построим по выборке «оценку» для этой функции.
Определение 1.
Эмпирической функцией распределения, построенной по выборке $IMAGE82$объема  , называется случайная функция $IMAGE84$, при каждом $IMAGE85$равная
, называется случайная функция $IMAGE84$, при каждом $IMAGE85$равная
$IMAGE86$
Напоминание: Случайная функция
$IMAGE87$
называется индикатором события $IMAGE88$. При каждом $IMAGE89$это — случайная величина, имеющая распределение Бернулли с параметром $IMAGE90$. почему?
Иначе говоря, при любом $IMAGE89$значение $IMAGE92$, равное истинной вероятности случайной величине 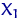 быть меньше $IMAGE89$, оценивается долей элементов выборки, меньших $IMAGE89$.
быть меньше $IMAGE89$, оценивается долей элементов выборки, меньших $IMAGE89$.
Если элементы выборки 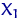 , $IMAGE30$, $IMAGE35$упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом:
, $IMAGE30$, $IMAGE35$упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом:
$IMAGE99$
Здесь
$IMAGE100$
Элемент $IMAGE101$, $IMAGE102$, называется $IMAGE50$-м членом вариационного ряда или $IMAGE50$-й порядковой статистикой.
Пример 1.
Выборка: $IMAGE105$
Вариационный ряд: $IMAGE106$
| Рис. 1. Пример 1 |
| $IMAGE107$ |
Эмпирическая функция распределения имеет скачки в точках выборки, величина скачка в точке $IMAGE108$равна $IMAGE109$, где $IMAGE110$— количество