Министерство образования Российской Федерации

Муниципальное общеобразовательное учреждение

"Средняя общеобразовательная школа №22"

Квадратные уравнения и уравнения высших порядков

Выполнили:

Ученики 8 "Б" класса

Кузнецов Евгений и Руди Алексей

Руководитель:

Зенина Алевтина Дмитриевна

преподаватель математики

Тюмень

2005

Оглавление

Введение

Глава 1. История квадратных уравнений и уравнений высших порядков

1.1 Уравнения в Древнем Вавилоне

1.2 Уравнения арабов

1.3 Уравнения в Индии

Глава 2. Теория квадратные уравнения и уравнения высших порядков

2.1 Основные понятия

2.2 Формулы четного коэффициента при х

2.3 Теорема Виета

2.4 Квадратные уравнения частного характера

2.5 Теорема Виета для многочленов (уравнений) высших степеней

2.6 Уравнения, сводимые к квадратным (биквадратные)

2.7 Исследование биквадратных уравнений

2.8 Формулы Кордано

2.9 Симметричные уравнения третьей степени

2.10 Возвратные уравнения

2.11 Схема Горнера

Заключение

Список используемой литературы

Приложение 1

Приложение 2

Приложение 3

Введение

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).

В этом реферате хотелось бы отобразить формулы и способы решения различных уравнений. Для этого приводятся уравнения, которые не изучаются в школьной программе. В основном это уравнения частного характера и уравнения высших степеней. Чтобы раскрыть эту тему приводятся доказательства этих формул.

Задачи нашего реферата:

- улучшить навыки решения уравнений

- наработать новые способы решения уравнений

- выучить некоторые новые способы и формулы для решения этих уравнений.

Объект исследования - элементарная алгебра Предмет исследования уравнения. Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.

Глава 1. История квадратных уравнений и уравнений высших порядков

1.1 Уравнения в Древнем Вавилоне

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведённых над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучается общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решением, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратного уравнения.

1.2 Уравнения арабов

Некоторые способы решения уравнений как квадратных, так и уравнений высших степеней были выведены арабами. Так известный арабский математик Ал-Хорезми в своей книге «Ал - джабар» описал многие способы решения различных уравнений. Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.

1.3 Уравнения в Индии

Квадратные уравнения решали и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 году индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII век), изложил общее правило решения квадратных уравнений, приведенных к единой конической форме:

aх² + bx = c, где a > 0

В этом уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи ». Задачи часто облекались в стихотворную форму.

Различные уравнения как квадратные, так и уравнения высших степеней решались нашими далекими предками. Эти уравнения решали в самых разных и отдаленных друг от друга странах. Потребность в уравнениях была велика. Уравнения применялись в строительстве, в военных делах, и в бытовых ситуациях.

Глава 2. Квадратные уравнения и уравнения высших порядков

2.1 Основные понятия

Квадратным уравнением называют уравнения вида

ax²+bx+c = 0,

где коэффициенты a, b, c – любые действительные числа, причём a ≠ 0.

Квадратное уравнение называют приведённым, если его старший коэффициент равен 1.

Пример:

x² + 2x + 6 = 0.

Квадратное уравнение называют не приведенным, если старший коэффициент отличен от 1.

Пример:

2x² + 8x + 3 = 0.

Полное квадратное уравнение - квадратное уравнение, в котором присутствуют все три слагаемых, иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля.

Пример:

3x² + 4x + 2 = 0.

Неполное квадратное уравнение – это квадратное уравнение, у которого хотя бы один коэффициент b, c равен нулю.

Таким образом, выделяют три вида неполных квадратных уравнений:

1) ax² = 0 (имеет два совпадающих корня x = 0).

2) ax² + bx = 0 (имеет два корня x₁ = 0 и x₂ = - )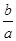

Пример:

x² + 5x = 0

x(x+5) =0

x₁= 0, x₂ = -5.

Ответ: x₁=0, x₂= -5.

3) ax² + c = 0

Если – <0 - уравнение не имеет корней.

Пример:

5x² + 6 = 0

Ответ: уравнение не имеет корней.

Если – > 0, то x_1,2 = ±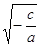

Пример:

2x² – 6 = 0

х²=±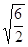

х_1,2=± $IMAGE6$

Ответ: х_1,2=± $IMAGE6$

Любое квадратное уравнение можно решить через дискриминант (b² - 4ac). Обычно выражение b² - 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)

Пример:

х² +14x – 23 = 0

D = b² – 4ac = 144 + 92 = 256

x_1,2 = $IMAGE8$

x₁ = $IMAGE9$

x₂ = $IMAGE10$

Ответ: x₁ = 1, x₂ = - 15.

В зависимости от дискриминанта уравнение может иметь или не иметь решение.

1) Если D < 0, то не имеет решения.

2) Если D = 0, то уравнение имеет два совпадающих решения x_1,2 = $IMAGE11$

3) Если D > 0, то имеет два решения, находящиеся по формуле:

x_1,2 = $IMAGE12$

2.2 Формулы четного коэффициента при х

Мы привыкли к тому, что корни квадратного уравнения

ax² + bx + c = 0 находятся по формуле

x_1,2 = $IMAGE12$

Но математики никогда не пройдут мимо возможности облегчить себе вычисления. Они обнаружили, что эту формулу можно упростить в случае, когда коэффициент b имеет вид b = 2k, в частности, если b есть четное число.

В самом деле, пусть у квадратного уравнения ax² + bx + c = 0 коэффициент b имеет вид b = 2k. Подставив в нашу формулу число 2k вместо b, получим:

x_1,2= $IMAGE14$

= $IMAGE15$

Итак, корни квадратного уравнения ax² + 2kx + c = 0 можно вычислять по формуле:

x_1,2= $IMAGE16$

Пример:

5х² - 2 $IMAGE17$х + 1 = 0

x_{1,2= $IMAGE18$}

Преимущество этой формулы в том, что в квадрат возводится не число b, а его половина, вычитается из этого квадрата не 4ac, а просто ac и, наконец, в том, что в знаменателе содержится не 2a, а просто a.

В случае если квадратное уравнение приведенное, то наша формула будет выглядеть так:

x_1,2=-k ± $IMAGE19$.

Пример:

х² – 4х + 3 = 0

х_1,2 = 2 ± $IMAGE20$

х₁ = 3

х₂ = 1

Ответ: х₁ = 3, х₂ = 1.

2.3 Теорема Виета

Очень любопытное свойство корней квадратного уравнения обнаружил французский математик Франсуа Виет. Это свойство назвали теорема Виета:

Чтобы числа x₁ и x₂ являлись корнями уравнения:

ax² + bx + c = 0

необходимо и достаточно выполнения равенства

x₁ + x₂ = -b/a и x₁x₂ = c/a

Теорема Виета позволяет судить о знаках и абсолютной величине квадратного уравнения

А именно

x² + bx + c = 0

1. Если b>0, c>0 то оба корня отрицательны.

2. Если b<0, c>0 то оба корня положительны.

3. Если b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.

4. Если b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.

2.4 Квадратные уравнения частного характера

1) Если a + b + c = 0 в уравнении ax² + bx + c = 0, то

х₁=1, а х₂ = .

Доказательство:

В уравнении ax² + bx + c = 0, его корни

x_1,2 = $IMAGE12$ (1).

Представим b из равенства a + b + c = 0

Подставим это выражение в формулу (1):

х_1,2= $IMAGE23$

= $IMAGE24$

Если рассмотрим по отдельности два корня уравнения, получим:

1) х₁= $IMAGE25$

2) х₂= $IMAGE26$

Отсюда следует: х₁=1, а х₂ = .

1. Пример:

2х² - 3х + 1 = 0

a = 2, b = -3, c = 1.

a + b + c = 0, следовательно

х₁ = 1

х₂ = ½

2. Пример:

418х² - 1254х + 836 = 0

Этот пример очень тяжело решить через дискриминант, но, зная выше приведенную формулу его с легкостью можно решить.

a = 418, b = -1254, c = 836.

х₁ = 1 х₂ = 2

2) Если a - b + c = 0, в уравнении ax² + bx + c = 0, то:

х₁=-1, а х₂ =- .

Доказательство:

Рассмотрим уравнение ax² + bx + c = 0, из него следует, что:

x_1,2 = $IMAGE12$ (2).

Представим b из равенства a - b +