База рефератов

Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса

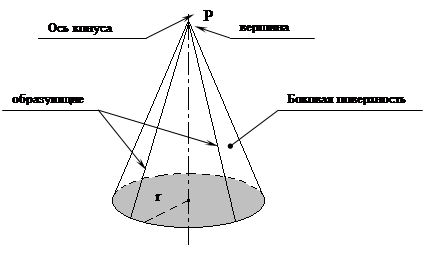
Получение конуса: конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

С

С2

С1

А

                       

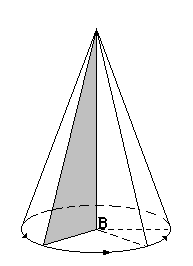
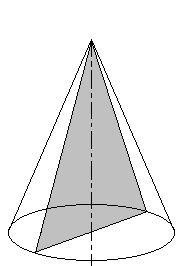
Сечение конуса: если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.

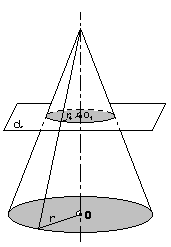
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О₁, расположенной на оси конуса.

Площадь поверхности конуса: разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора – длине окружности основания конуса. За площадь боковой поверхности конуса принимается площадь ее развертки.

$IMAGE6$

А1

В

А

Р

В

А

Р

                                   $IMAGE7$

где α – градусная мера дуги АВА₁

$IMAGE8$           $IMAGE9$

откуда $IMAGE10$ $IMAGE8$     

$IMAGE12$

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

$IMAGE13$

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

Усеченный конус, его получение и площадь:

образующая

$IMAGE14$ $IMAGE15$

конуса

Основания

поверхность

боковая

$IMAGE16$ $IMAGE17$ $IMAGE18$ $IMAGE19$ $IMAGE20$

Р

                  $IMAGE21$

Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

$IMAGE22$

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.