База рефератов

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

"ВЛАДИМИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"

Кафедра: Функциональный анализ и его приложения

Самостоятельная работа по математике

Владимир 2009

Задача 1. Коллинеарность векторов

а = { 2; -1; 6 }     в = { -1; 3; 8 }

c₁=5a – 2b = {5*2 – 2*(-1); 5*(-1) – 2*3; 5*6-2*8 } = {12; -11; 14 }

с₂=2а – 5в = {2*2 – 5*(-1); 2*(-1) – 5*3; 2*6-5*8 } = {9; -17; -28 }

 ≠  ≠-

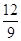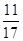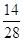
12/9 ≠ 11/17 ≠ -14/28

Ответ: не коллинеарны.

Задача 2. Косинус угла между векторами АВ и АС

А (3; 3; -1 ) B (5; 1; -2 ) C (4; 1; -3 )

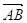 = {2; -2; -1 } | 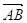| = $IMAGE7$ = $IMAGE8$

$IMAGE9$ = {1; -2; -2 } | $IMAGE9$| = $IMAGE11$ = $IMAGE8$

cos ( 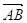ˆ $IMAGE9$) = $IMAGE15$= $IMAGE16$

Задача 3. Площадь параллелограмма построенного на векторах а и в.

а=5p-q       b=p+q        |p|=5 |q|=3  (pˆq) = 5 $IMAGE17$

S=|5p - q|*|p + q|=|5p*p + 5p*q - q*p - q*q|=|5p*q + p*q| =6*|p*q|=6|p|*|q|*sin(pˆq)=

=6*5*3*sin5 $IMAGE17$

sin5 $IMAGE17$= $IMAGE20$   90* $IMAGE20$=45

Задача 4. Компланарность векторов а, в, с.

а = { 1; -1; 4 } в = { 1; 0; 3 } с = { 1; -3; 8 }

$IMAGE22$

1*(0*8 - 3*(-3)) - (-1)*(1*8 - 1*3)+4(1*(-3) - 1*0)=9 + 5 - 12=2

2≠0 - не компланарны.

Задача 5. Объем тетраэдра с вершинами в точках А₁ А₂ А₃ А₄ и его высоту, опущенную из вершины А₄на грань А₁ А₂ А₃.

А₁ = { 0; -3; 1 } А₂ = { -4; 1; 2 } А₃ = { 2; -1; 5 } А₄ = { 3; 1; -4 }

$IMAGE23$₌ { -4; 4; 1 }

$IMAGE24$₌ { 2; 2; 4 }

$IMAGE25$₌ { 3; 4; -5 }

$IMAGE26$

= $IMAGE27$* |(-4)*(2*(-5) - 4*4) - 4*(2*(-5) - 3*4) + 1*(2*4 - 3*2)=

= $IMAGE27$|40 + 64 + 40 + 48 + 8 - 6|= $IMAGE27$194=32,33

$IMAGE30$

= $IMAGE20$|i*(4*4 - 1*2) - j*((-4)*4 - 2*1)+k*((-4)*2 - 2*4)= $IMAGE20$|14i + 18j - 16k|=

= $IMAGE20$√14²+18²-16²= $IMAGE20$√264= $IMAGE20$*16,25=8,125

h= $IMAGE36$=11,94

Задача 6. Расстояние от точки М₀ до плоскости, проходящей через три точки

$IMAGE37$.

М₁ (1; 2; 0 ) М₂ (3; 0; -3 ) М₃ (5; 2; 6 ) М₀ (-13; -8; 16 )

$IMAGE38$

(х-1) * ((-2)*6 - 0*(-3)) - (у-2)*(2*6 - 4*(-3)) + (z - 0)*(2*0 - 4*(-2))=0

(-12)*(х - 1) - 24*(у - 2) + 8*(z - 0) = 0

(-3)*(х - 1) - 6*(у - 2) + 2*(z - 0)=0

-3х - 6у + 2Z + 15 = 0

d= $IMAGE39$= $IMAGE40$

Задача 7. Уравнение плоскости, проходящей через точку А перпендикулярно вектору $IMAGE41$.

А (-3; -1; 7 ) B (0; 2; -6 ) C (2; 3; -5 )

$IMAGE41$={2; 1; 1}

2*(х + 3) + 1*(у + 1) + 1*(z - 7)=0

2х + у + z = 0

Задача 8. Угол между плоскостями

2у + z - 9=0

х - у + 2z - 1=0

п₁={0; 2; 1 }

п2={1; -1; 2 }

cosφ= $IMAGE43$= $IMAGE44$=90 $IMAGE45$

Задача 9. Координаты точки А, равноудаленной от точек В и С.

А (х; 0; 0 ) B (4; 5; -2 ) C (2; 3; 4 )

АВ= $IMAGE46$= $IMAGE47$= $IMAGE48$

АС= $IMAGE49$= $IMAGE50$= $IMAGE51$

$IMAGE48$= $IMAGE51$

$IMAGE54$=х² - 4х+29

х² - х² - 8х + 4х=29 – 45

-4х=-16

х=4

А (4; 0; 0 )

Задача 10. Канонические уравнения прямой

х - 3у + z + 2 = 0

х + 3у + 2z + 14 = 0

$IMAGE55$

= i*((-3)*2 - 3*1)-j*(1*2 - 1*1)+k*(1*3 - 1*(-3) = -9i -j + 6k=

$IMAGE56$= { -9; -1; 6}

$IMAGE57$

$IMAGE58$ (-8; 0; 0 )         $IMAGE59$ = $IMAGE60$ = $IMAGE61$

Задача 11. Точка пересечения прямой и плоскости

$IMAGE62$ = $IMAGE63$ = $IMAGE64$

3х – 2у + 5z – 3 = 0

$IMAGE62$ = $IMAGE63$ = $IMAGE64$ = t

$IMAGE68$

3*(1 + 6t) - 2*(3 + t) + 5*((-5) + 3t) – 3 = 0

3 + 18t – 6 - 2t – 25 + 15t – 3 = 0

31t – 31 = 0

31t = 31

t = 1

х = 1 + 6*1 у = 3 + 1    z = (-5) + 3*1

х = 7 у = 4 z = -2

( 7; 4; -2 )