Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Комсомольский-на-Амуре государственный
технический университет»
Факультет компьютерных технологий
Кафедра «Информационных систем»
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
по дисциплине «Дискретная математика»
Студент группы 9-ПИ Шикер С.А.
2010
Задача 1. Представьте заштрихованные области диаграммы Эйлера-Венна (рис.1) максимально компактным аналитическим выражением, в котором используется минимальное количество операций и букв.
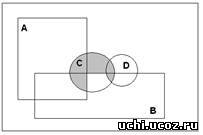
рис.1
Решение
На рис.2 изображена диаграмма Эйлера-Венна, заштрихованные области которой соответствуют выражению: C∩D. На рис.3 изображена диаграмма Эйлера-Венна, заштрихованные области которой соответствуют выражению: C/B. На рис.4 изображена диаграмма Эйлера-Венна, заштрихованные области которой соответствуют выражению: C∩А.
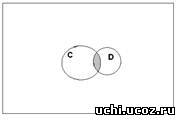
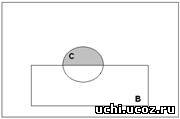
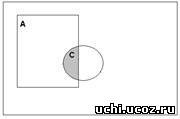 Рис. 2 Рис. 3 Рис.4
Рис. 2 Рис. 3 Рис.4
Чтобы получить необходимое множество (рис. 1) необходимо между этими тремя выражениями поставить операцию объединение. В результате получаем:
(C∩D) È (C/B) È (C∩A)
Задание 2. Записать высказывание в виде формулы логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких – либо других высказываний:
Неверно, что если Сидоров - не кассир, то Сидоров убил кассира; следовательно, фамилия кассира – Сидоров.
Решение
Введем обозначения:
a – «Сидоров – кассир»
b – «Сидоров убил кассира»
Исходное высказывание содержит связку «если …, то …», которая соответствует импликации, а так же связку «Неверно, что…» и предлог «не», что соответствует отрицанию. Формула имеет вид:
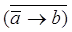 → a
→ a
Задание 3. Используя равносильности логики высказываний, упростить исходную формулу
$IMAGE6$
Для исходной формулы и упрощенной построить таблицу истинности.
Решение.
$IMAGE7$ $IMAGE8$
Введем обозначения: F1 = $IMAGE9$
F2 = $IMAGE10$
Построим таблицу истинности для F1 и F2:
| № | a | b | c | $IMAGE11$ | $IMAGE12$ | $IMAGE13$ | $IMAGE14$ | F1 | $IMAGE15$ | F2 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Столбцы, соответствующие F1 и F2, совпадают. Это значит, что аналитические преобразования исходной формулы верны.
Задание 4. Ниже приведена клауза $IMAGE16$
$IMAGE17$
Необходимо выяснить при помощи алгоритма Вонга и метода резолюции является ли клауза теоремой.
Решение
Метод Вонга.
Построим дерево доказательства.
$IMAGE18$ $IMAGE18$ $IMAGE20$
$IMAGE21$
$IMAGE22$
$IMAGE23$ $IMAGE24$ $IMAGE25$
$IMAGE26$ $IMAGE27$
$IMAGE28$
$IMAGE29$ $IMAGE30$ $IMAGE31$ $IMAGE23$ $IMAGE33$ $IMAGE34$
$IMAGE35$
$IMAGE36$
$IMAGE37$
$IMAGE38$ $IMAGE39$
$IMAGE42$ $IMAGE43$
$IMAGE26$ $IMAGE26$ $IMAGE46$ $IMAGE46$ $IMAGE48$ $IMAGE49$ $IMAGE50$
$IMAGE51$
$IMAGE52$ $IMAGE53$
$IMAGE54$ $IMAGE55$
Все ветви дерева заканчиваются клаузами, в которых по обеим сторонам символа $IMAGE56$присутствует одна и та же буква. Следовательно, логическая теорема верна.
Метод резолюция.
$IMAGE17$
Необходимо преобразовать клаузу таким образом, чтобы после знака $IMAGE58$ получился ноль, при этом избавимся от импликации.
$IMAGE59$Ǿ
Выпишем по порядку все посылки и далее начнем их «склеивать».
| 1 | $IMAGE60$ | 7 | (2;3)А |
| 2 | $IMAGE61$ | 8 | (1;5) $IMAGE62$ |
| 3 | $IMAGE63$ | 9 | (7;4) $IMAGE64$ |
| 4 | $IMAGE65$ | 10 | (9;6)B |
| 5 | $IMAGE66$ | 11 | (10;8)Ǿ |
| 6 | $IMAGE67$ | | |
Иначе, порядок «склеивания» можно представить в виде цепочки равносильных преобразований:
$IMAGE68$
Задание 5. Заданы номера наборов аргументов, на которых булева функция принимает значение, равное единице. Необходимо:
· Записать булеву функцию в СДНФ и СКНФ;
· Минимизировать функцию с помощью минимизационной карты;
· Построить алгоритм Куайна.
· Выяснить к каким функционально-замкнутым классам принадлежит булева функция;
·
f (x1,x2,x3,x4)=1010010010110011
Решение
1. Запишем СДНФ и СКНФ булевой функции.
СДНФ(1):№ 0,2,5,8,10,11,14,15
f = $IMAGE69$1 $IMAGE69$2 $IMAGE71$3 $IMAGE72$4 $IMAGE73$1 $IMAGE74$2 $IMAGE75$3 $IMAGE76$4 $IMAGE77$1 $IMAGE78$2 $IMAGE71$3 $IMAGE78$4 $IMAGE81$1 $IMAGE82$2 $IMAGE71$3 $IMAGE84$4 $IMAGE85$
$IMAGE86$1 $IMAGE84$2 $IMAGE88$3 $IMAGE71$4 $IMAGE86$1 $IMAGE71$2 $IMAGE88$3 $IMAGE88$4 $IMAGE94$1 $IMAGE88$2 $IMAGE88$3 $IMAGE71$4 $IMAGE98$1 $IMAGE88$2 $IMAGE88$3 $IMAGE88$4
СКНФ(0):№ 1,3,4,6,7,9,12,13
f = ( $IMAGE102$1 $IMAGE103$2 $IMAGE86$3 $IMAGE105$4) ( $IMAGE106$1 $IMAGE86$2 $IMAGE77$3 $IMAGE77$4) ( $IMAGE102$1 $IMAGE111$2 $IMAGE112$3 $IMAGE112$4) ( $IMAGE88$1 $IMAGE115$
$IMAGE116$2 $IMAGE117$3 $IMAGE112$4) ( $IMAGE119$1 $IMAGE111$2 $IMAGE77$3 $IMAGE77$4) ( $IMAGE82$1 $IMAGE112$2 $IMAGE112$3 $IMAGE126$4) ( $IMAGE71$1 $IMAGE128$
$IMAGE129$2 $IMAGE112$3 $IMAGE131$4) ( $IMAGE71$1 $IMAGE129$2 $IMAGE134$3 $IMAGE135$4)
2. Строим минимизационную карту и пошагово выполняем алгоритм.
Шаг1.
| № | x1 | x2 | x3 | x4 | x1x2 | x1x3 | x1x4 | x2x3 | x2x4 | x3x4 | x1x2x3 | x1x2x4 | x1x3x4 | x2x3x4 | x1x2x3x4 | f |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 2 | 1 | 0 | |