Мера ограниченного открытого множества

В теории функций вещественной переменной большую роль играет понятие меры точечного множества, обобщающее понятие длины промежутка, площади прямоугольника, объема параллелепипеда и т.д. В этой главе мы изложим теорию измерения линейных ограниченных точечных множеств, принадлежащую А.Лебегу.

Так как наиболее простой структурой обладают открытые множества, то естественно начать именно с них.

Определение 1. Мерой интервала (a, b) называется его длина, т.е. b - a. Это число обозначается так:

m (a, b) = b - a

Очевидно, что всегда m (a, b) > 0.

Лемма 1. Если в интервале D содержится конечное число взаимно не налегающих интервалов d₁, d₂, ..., d_n, то

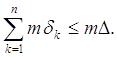
Д о к а з а т е л ь с т в о.  Пусть D = (A, B), d_k = (a_k, b_k) (k = 1, 2, …, n).

Не нарушая общности, можно считать, что интервалы d_k перенумерованы в порядке возрастания левых концов, т.е. что

a₁ < a₂ < … < a_n.

Но тогда, очевидно, b_k £ a_k+1 (k = 1, 2, …, n - 1), ибо иначе интервалы d_k и d_k+1 налегали бы друг на друга. Поэтому сумма

Q = (B - b_n) + (a_n - b_n-1) + … + (a₂ - b₁) + (a₁ - A)

не отрицательна. Но очевидно, что 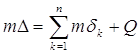 , откуда и следует лемма.

Следствие. Если на интервале D лежит счетное множество взаимно не налегающих интервалов d_k (k = 1, 2, 3, …), то

.

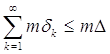[Имея дело с положительным расходящимся рядом, мы приписываем ему сумму, равную + ¥; поэтому всякий положительный ряд имеет некоторую сумму. Неравенства 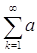_k< C (положительного ряда) гарантирует его сходимость.]

Определение 2. Мерой mG непустого открытого ограниченного множества G называется сумма длин  всех его составляющих интервалов  d_k:

$IMAGE6$

 (Не зная, конечно или счетно множество {d_k}, мы будем употреблять обозначение $IMAGE7$d_k, подразумевая, смотря по обстоятельствам, под этим символом $IMAGE9$_k  или  $IMAGE10$_k.)

В силу вышеотмеченного следствия,

mG< + ¥

Если  множество G пусто, то мы , по определению, полагаем

mG=0,

так что всегда mG³0.

Если D есть интервал, содержащий в себе открытое множество G, то

mG £  mD,

что вытекает из того же следствия.

Пример (Канторово множество G₀). Построение Канторова множества G₀ состояло из ряда последовательных шагов.

На первом шагу брался  интервал (1/3, 2/3) длины 1/3. На втором шагу к нему присоединялись два интервала: (1/9, 2/9) и (7/9, 8/9), длины 1/9 каждый.

На третьем шагу присоединялись еще четыре интервала, длины 1/27 каждый и т.д.

Таким образом

mG₀ = $IMAGE12$… $IMAGE13$

Суммируя по известной формуле эту прогрессию, получаем

mG₀ = 1.

Теорема 1. Пусть G₁ и  G₂  два ограниченных открытых множества. Если  G₁ Ì  G₂, то

mG₁ £  mG₂.

Д о к а з а т е л ь с т в о. Пусть d_i (i = 1, 2, …) и D_k (k = 1, 2, …) суть, соответственно, составляющие интервалы множеств G₁ и  G₂.

В силу теоремы 4, § 5, гл.II, каждый из интервалов d_i  содержится в одном (и только одном) из интервалов D_k.

Поэтому множество {d_i} можно разбить на ряд взаимно не пересекающихся подмножеств А₁, А₂, А_3,…, относя d_i в А_k в том случае, когда d_i Ì D_k.

Тогда, пользуясь известными свойствами двойных рядов, мы можем написать

$IMAGE14$.

Но, в силу следствия леммы 1,

$IMAGE15$, откуда $IMAGE16$,

что и требовалось доказать.

Следствие. Мера открытого ограниченного множества G есть точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих G.

Теорема 2. Если открытое ограниченное множество G является суммой конечного числа или счетного множества взаимно не налегающих открытых множеств

$IMAGE17$,

то

$IMAGE18$.

Это свойство меры называется полной аддитивностью.

Д о к а з а т е л ь с т в о. Пусть $IMAGE19$ (i = 1, 2, …) суть составляющие интервалы множества G_k. Покажем, что каждый из них является составляющим интервалом суммы G.

В самом деле, то обстоятельство, что $IMAGE20$G, очевидно. Остается убедиться, что концы интервала $IMAGE21$ не принадлежат G. Допустим, что, например, правый конец интервала $IMAGE22$ принадлежит G. Тогда этот правый конец (обозначим его через m) должен принадлежать какому-нибудь из слагаемых множеств. Пусть m Î G_k'. (Очевидно k¢ ¹ k, ибо множеству G_k точка m заведомо не принадлежит.) Но множество G_k¢ открыто и, стало быть, точка m принадлежит одному из составляющих интервалов этого множества m Î d_i¢^(k¢⁾. Однако это влечет за собой то, что интервалы d_i^(k)  и d_i¢^(k¢⁾  пересекаются, последнее же противоречит условию G_k G_k¢= 0.

Итак, действительно, каждый из d_i^(k) есть составляющий интервал множества G. С другой стороны, каждая точка G принадлежит хоть одному d_i^(k) . Наконец, все эти интервалы различны. Таким образом, множество

$IMAGE23$           (i = 1, 2, …;   k = 1, 2, …)

есть множество всех составляющих интервалов суммы G.

Установив это, уже легко закончить доказательство:

$IMAGE25$= $IMAGE26$ $IMAGE27$

что и требовалось доказать.

Для того чтобы перенести теорему (соответственно изменить ее) на случай суммы  п е р е с е к а ю щ и х с я  слагаемых, нам понадобятся две простые леммы.

Лемма 2. Пусть сегмент [P, Q] покрыт конечной системой  Н интервалов (l, m ). Тогда

$IMAGE29$

Д о к а з а т е л ь с т в о. Выделим из системы Н некоторую ее часть Н*, которая строится следующим образом: обозначим через (l_{1, $IMAGE30$}) какой-нибудь из интервалов системы H, содержащих точку P

l₁ < P < m₁

(хоть один такой интервал существует). Если  окажется, что m₁>Q, то интервал (l_1, m₁) , и составляет требуемую систему H^* . Если же m_{1 $IMAGE31$}Q, то m₁Î[P, Q], и можно в системе H найти интервал ( l₂, m₂), содержащий точку m_{1 ,}

l₂ <  m₁ < m₂

Если окажется, что m₂>Q, то процесс окончен, и интервалы (l_1, m₁) и ( l₂, m₂) и составляют систему Н*.

Если же m_{2 $IMAGE31$}Q, то m₂Î[P, Q], и можно в системе H найти интервал ( l₃, m₃), содержащий m₂.

l₃ <  m₂ < m₃

Если m₃>Q, то процесс закончен, а если m_{3 $IMAGE31$}Q, то продолжаем наш процесс.

Но ведь множество H по условию конечно, а наш процесс состоит в выделении из H все новых и новых интервалов, ибо

m₁ <  m₂ < m₃ < …

Поэтому процесс обязательно должен закончится, а конец его состоит в том, что какая-то из точек m_k окажется лежащей правее точки Q.

Пусть m_n>Q, но m_n-1£Q, т.е. процесс заканчивается после n-го шага.

Тогда интервалы (l_1, m₁), ( l₂, m₂), … , (l_n, m_n) и составляют систему H. При этом l_k+1<m_k (k = 1, 2, … , n-1).

Значит

$IMAGE34$

а так как m_n - l₁ > Q – P, то Q – P < $IMAGE35$, откуда и подавно

Q – P < $IMAGE36$.

Лемма 3. Пусть интервал D есть сумма конечного или счетного множества открытых множеств

D = $IMAGE37$.

Тогда

mD $IMAGE38$.

Д о к а з а т е л ь с т в о. Пусть D = (A, B) и пусть составляющие интервалы множества G_k суть d_i^(k) (i = 1, 2, …).

Возьмем положительное число e (0 < e < $IMAGE39$) и рассмотрим сегмент $IMAGE40$, содержащийся в  интервале D.

Этот сегмент покрыт системой интервалов d_i^(k) (i = 1, 2, …; k = 1, 2, …). Применяя к этой системе теорему Бореля о конечном покрытии из § 2, гл. II, мы получим некоторую конечную систему

$IMAGE41$         (s = 1, 2, … n),

покрывающую сегмент $IMAGE42$. В силу предыдущей леммы, $IMAGE43$, откуда и подавно

B – A - 2e < $IMAGE44$.

Так как число e произвольно мало, то

B – A $IMAGE45$,

и лемма доказана.

Теорема 3. Если открытое ограниченное множество G является суммой конечного числа или счетного множества открытых множеств G_k, G = $IMAGE46$, то

mG $IMAGE47$.

Д о к а з а т е л ь с т в о. Пусть D_i (i = 1, 2, …) суть составляющие интервалы суммы G. Тогда mG = $IMAGE48$.

Но $IMAGE49$ откуда, в силу леммы 3, $IMAGE50$и, стало быть,

     

$IMAGE51$               (*)

С другой стороны $IMAGE52$

При этом (что является здесь основным) отдельные слагаемые правой части взаимно не пересекаются (потому что $IMAGE53$ при i¹i`). Значит, мы находимся в условиях применимости теоремы 2, а потому

                                                         

$IMAGE54$                   (**)

Сопоставляя (*) и (**), мы и получаем теорему.

Мера ограниченного замкнутого множества

Пусть F непустое ограниченное замкнутое множество и S наименьший сегмент, содержащий множество F. Как известно, множество C_SF открыто и поэтому имеет определенную меру $IMAGE55$m[C_SF]. Это дает возможность установить следующее определение.

Определение 1. Мерой непустого ограниченного замкнутого множества F называется число

$IMAGE56$

где S=[A, B] есть наименьший сегмент, содержащий множество F.

Для пустого замкнутого множества меру определять не нужно, ибо такое множество открыто и мерой его мы уже условились считать число 0. Кроме того, непустое замкнутое ограниченное множество не может оказаться открытым множеством, так что нет надобности ставить вопрос о связи определений меры открытого и замкнутого множества.

Рассмотрим некоторые примеры.

1. F=[a, b]. В этом случае, очевидно, S=[a, b] и C_sF=0, так, что m [a, b] = b – a, т. е. мера сегмента равна его длине.

2. F есть сумма конечного числа попарно не пересекающихся сегментов $IMAGE57$

Можно считать, что сегменты перенумерованы в порядке возрастания левых концов; тогда, очевидно,

$IMAGE58$         (k=1, 2, … n-1),

откуда следует, что

$IMAGE59$       $IMAGE60$

Стало быть,

$IMAGE61$

т.е. мера суммы конечного числа попарно не пересекающихся сегментов равна сумме длин этих сегментов.

     3. Пусть $IMAGE62$ (Канторово совершенное множество). В этом случае

$IMAGE64$  и  $IMAGE65$ откуда

$IMAGE66$

т.е. Канторово совершенное множество $IMAGE67$ имеет меру нуль. Этот факт интересно сопоставить с тем, что мощность множества $IMAGE67$ есть с.

    Теорема 1. Мера ограниченного замкнутого множества F не отрицательна.

    Д о к а з а т е л ь с т в о.  Действительно, если пользоваться обозначениями определения 1, то очевидно $IMAGE69$Ì (А, В), и по теореме 1, $IMAGE70$ откуда и следует, что $IMAGE71$

    Лемма. Пусть F ограниченное замкнутое множество, содержащееся в интервале D, тогда

$IMAGE72$D- [ C_DF]

     Д о к а з а т е л ь с т в о. Множество C_DF – открыто, так что лемма имеет смысл. Пусть D=(A, B), а наименьший сегмент, содержащий множество F, есть S=[a, b] (рис.1.).