База рефератов

Курсовая работа

Иррациональные уравнения

Содержание:

Введение

1. Основные определения и теоремы

2. Стандартные иррациональные уравнения и методы их решения

2.1 Уравнения вида

2.2. Уравнения вида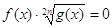

2.3 Иррациональные уравнения, которые решаются введением новой переменной

2.4 Уравнения вида , ,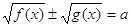

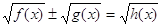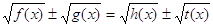
3. Нестандартные методы решения иррациональных уравнений

3.1 Применение основных свойств функции

3.1.1 Использование области определения уравнения

3.1.2 Использование области значений функции

3.1.3 Использование монотонности функции

3.1.4 Использование ограниченности функции

3.2 Применение производной

3.2.1 Использование монотонности функции

3.2.2 Использование наибольшего и наименьшего значений функций

4. Смешанные иррациональные уравнения и методы их решения

4.1 Иррациональные уравнения, содержащие двойную иррациональность

4.2 Иррациональные показательные уравнения

4.3 Иррациональные логарифмические уравнения

Заключение

Литература

Введение

Тема моей курсовой работы − «иррациональные уравнения». Я выбрала её потому, что в учебном курсе, этому материалу посвящено мало часов, а в задачниках большое количество примеров посвящено именно этой теме.

Поэтому в изучении «иррациональных уравнений» я преследую цель - дать основные определение иррациональным уравнениям и теоремам. Определить какие бывают виды уравнений. Рассмотреть правила решения иррациональных уравнений.

Задачи моей работы – изучить научную и методическую литературу, подобрать и рассмотреть задачи для данной темы, включая олимпиадные.

В моей курсовой работе показаны решения иррациональных уравнений как стандартного метода, так и не стандартного метода решения. Я старалась как можно доступнее охватить проблемы этой темы. Конечно, всё нельзя учесть в курсовой работе, но я постараюсь ниже изложить основные моменты. Я хотела бы сделать данную работу вспомогательным пособием при изучении темы «Иррациональные уравнения».

1. Основные определения и теоремы

Определение 1. Уравнение – это два выражения, соединенные знаком равенства; в эти выражения входит одна или несколько переменных, называемых неизвестными.

Пример 1. $IMAGE6$- является уравнением с одной неизвестной.

Пример 2. $IMAGE7$ - является уравнением с двумя неизвестными.

Определение 2. Равенство вида $IMAGE8$ называется уравнением с одной переменной $IMAGE9$.

Пример 1. $IMAGE10$ - является уравнением с одной переменной х.

Далее рассматриваем уравнения с одной переменной.

Определение 3. Всякое значение переменной, при котором выражения $IMAGE11$ и $IMAGE12$ принимают равные числовые значения, называется корнем уравнения или его решением.

Пример 1. Уравнение $IMAGE13$ имеет два корня: -1 и 1.

Определение 4. Решить уравнение – значит, найти множество всех его решений или доказать, что их нет.

Пример 1. Уравнение $IMAGE14$ имеет единственный корень 4, так как при этом и только при этом значении переменной $IMAGE14$ обращается в верное равенство, таким образом, ответ записывается в следующем виде:

О т в е т: {4}.

Пример 2. Уравнение $IMAGE16$ $IMAGE17$ не имеет действительных корней.

О т в е т: $IMAGE18$.

Пример 3. Уравнение $IMAGE19$ имеет бесконечное множество решений, так как после тождественных преобразований получили равенство $IMAGE20$. Т.е данное уравнение $IMAGE19$ есть тождественное равенство, верное для любого действительного значения $IMAGE9$.

О т в е т: $IMAGE23$.

Определение 5. Тождество (тождественное равенство) - это равенство двух выражений с переменными, верное при всех допустимых значениях входящих в него переменных. Тождествами считаются и верные числовые равенства, а также равенства, превращающиеся в верное числовое равенство для всех числовых значений букв, для которых эти выражения определены.

Пример 1. Равенство $IMAGE24$, справедливо для всех числовых значений $IMAGE25$и в, является тождественным.

Пример 2. Равенство 2=2 тождество.

Определение 6. Тождественное преобразование выражения – это замена выражения на тождественно равное ему выражение, т. е. равное для всех числовых значений входящих в него переменных.

К тождественным преобразованиям относятся, например, приведение подобных слагаемых; разложение на множители; приведение алгебраических дробей к общему знаменателю; разложение их на элементарные дроби и другие.

Определение 7. Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень.

Пример 1. $IMAGE26$ - иррациональное уравнение (переменная содержится под знаком радикала).

Пример 2. $IMAGE27$ иррациональное уравнение (переменная содержится под знаком возведения в дробную степень).

Определение 8. Областью определения уравнения (или областью допустимых значений переменной - ОДЗ) $IMAGE8$называют множество всех тех значений переменной $IMAGE9$, при которых и выражение $IMAGE11$, и $IMAGE12$имеют смысл.

Пример 1. $IMAGE32$ Выражение ( $IMAGE33$ и $IMAGE34$ определены при всех $IMAGE9$. Значит, ОДЗ: $IMAGE36$.

Пример 2. $IMAGE37$. Выражение $IMAGE38$ не определено при $IMAGE39$, а выражение $IMAGE40$ не определено при $IMAGE41$.

Значит, ОДЗ: $IMAGE42$.

Пример 3. $IMAGE43$. Корень четной степени имеет смысл лишь при неотрицательных значениях подкоренного выражения. Значит, одновременно должны выполняться условия: $IMAGE44$ т.е. ОДЗ: $IMAGE45$

Определение 9. Пусть даны уравнения: $IMAGE46$ (1), $IMAGE47$ (2).

Если каждый корень уравнения (1) является одновременно корнем уравнения (2), то уравнение (2) называется следствием уравнения (1). Следствие обозначается следующим образом: $IMAGE16$  $IMAGE49$

Пример 1. $IMAGE50$

В процессе решения уравнения часто приходится применять такие преобразования, которые приводят к уравнению, являющемуся следствием исходного. Уравнению-следствию удовлетворяют все корни исходного уравнения, но, кроме них, уравнение-следствие может иметь и такие решение, которые не являются корнями исходного уравнения, так называемые, «посторонние» корни. Чтобы выявить и отсеять «посторонние» корни, обычно поступают так: все найденные корни уравнения-следствия проверяют подстановкой в исходное уравнение.

Рассмотрим примеры преобразований, которые могут привести к расширению ОДЗ, т.е. к появлению «посторонних» корней.

1. Замена уравнения $IMAGE51$ уравнением $IMAGE52$

Если при некотором значении $IMAGE9$, равном $IMAGE54$, верно равенство $IMAGE55$, то верным является также равенство $IMAGE56$. Значит, уравнение $IMAGE56$ является следствием исходного уравнения. При этом может существовать такое значение $IMAGE9$, равное $IMAGE59$, при котором $IMAGE60$ и $IMAGE61$. Тогда число $IMAGE59$, являющееся корнем уравнения $IMAGE63$, не является корнем исходного уравнения, т.к. при $IMAGE64$ исходное уравнение не имеет смысла.

Пример 1. Решить уравнение $IMAGE65$.

Решение. $IMAGE66$. Тогда $IMAGE67$.

Проверка.

При $IMAGE68$ знаменатель уравнения не обращается в ноль, а при $IMAGE69$ - обращается. Следовательно, исходное уравнение имеет единственный корень: -10.

О т в е т: $IMAGE70$.

2. Возведение обеих частей уравнения в квадрат.

Пусть даны два уравнения $IMAGE8$ (1) и $IMAGE72$. Если $IMAGE54$- корень первого уравнения, то верно равенство $IMAGE74$. Из равенства двух чисел вытекает равенство их квадратов, т.е. $IMAGE75$, а это означает, что $IMAGE54$- корень уравнения (2). Значит из уравнения (1) следует уравнение (2).

В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.

Пример 1. Решить уравнение $IMAGE77$.

Решение. Возведем обе части этого уравнения в квадрат.

$IMAGE78$; $IMAGE79$.Тогда $IMAGE80$, $IMAGE81$.

Проверка.

Если $IMAGE82$, то $IMAGE83$, равенство не верно, следовательно, -1- не является корнем исходного уравнения.

Если $IMAGE84$, то 4=4, равенство верно.

Следовательно, уравнение имеет единственный корень: 4.

О т в е т: {4}.

3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.

Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения - следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.

Пример 1. Решить уравнение $IMAGE85$.

Решение. Выполнив приведение подобных слагаемых, получим: $IMAGE86$. Тогда $IMAGE87$, $IMAGE88$.

Проверка.

Если $IMAGE89$, то выражение $IMAGE90$ не имеет смысла.

Если $IMAGE91$, то $IMAGE92$, равенство верно.

Следовательно, уравнение имеет единственный корень:5.

О т в е т: {5}.

Пример 2. Решить уравнение $IMAGE93$.

Решение. $IMAGE94$ или $IMAGE95$. Тогда $IMAGE96$, $IMAGE97$.

Проверка.

Если $IMAGE98$, то выражение $IMAGE99$ не имеет смысла.

Если $IMAGE100$, то $IMAGE20$, равенство верно.

Следовательно, уравнение имеет единственный корень:-2.

О т в е т: {-2}.

Если при решении уравнения мы заменили его уравнением - следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.

Рассмотрим уравнение $IMAGE8$ (3) и умножим обе части его на одно и тоже выражение $IMAGE103$, имеющее смысл при всех значениях $IMAGE9$. Получим уравнение: $IMAGE105$ (4), корнями которого служат как корни уравнения (3), так и корни уравнения $IMAGE106$.

Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение $IMAGE107$ не имеет корней. Таким образом, справедлива следующая теорема.

Теорема 1. Если обе части уравнения умножить на $IMAGE103$, то получится уравнение, являющееся следствием исходного. Если уравнение $IMAGE106$ не имеет корней, то полученное уравнение равносильно исходному (если область допустимых значений $IMAGE103$не уже области допустимых значений переменной данного уравнения).

Пример 1. $IMAGE111$ .

Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение $IMAGE103$, как правило, недопустимо, поскольку можно привести к потери корней, в этом случае могут «потеряться» корни уравнения $IMAGE106$.

Пример 2. Уравнение $IMAGE114$ имеет два корня: 3 и 4.

Деление обеих частей уравнения на $IMAGE115$ приводит к уравнению $IMAGE116$, имеющий только один корень 4, т.е. произошла потеря корня.

Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение: $IMAGE117$ (5), корнями которого служат как корни уравнения (3), так и корни «постороннего» уравнения $IMAGE118$. Ясно, что уравнения (3) и (5) равносильны, если у «постороннего» уравнения нет корней.

Пример 3. Уравнение $IMAGE119$ имеет корень 4. Если обе части этого уравнения возвести в квадрат, то получится уравнение $IMAGE120$, имеющие два корня: -2 и 4. Значит, уравнение $IMAGE121$- следствие уравнения $IMAGE119$. При переходе от уравнения $IMAGE119$к уравнению $IMAGE121$ появился «посторонний» корень: -2.

Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.

Пример 1. $IMAGE125$.

При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.

Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: $IMAGE126$.

Пример 1. Уравнения $IMAGE127$ и $IMAGE128$ равносильны, т.к. каждое из них имеет единственный корень – число 3. $IMAGE127$ $IMAGE130$ $IMAGE128$.

Пример 2. Уравнения $IMAGE132$ и $IMAGE133$ не равносильны, т.к. первое имеет только один корень: 6, а второе имеет два корня: 6 и -6.

Пример 3. Уравнения $IMAGE134$ и $IMAGE135$ равносильны, т.к. множества их решений пусты. $IMAGE134$ $IMAGE130$ $IMAGE135$.

Определение 11. Пусть даны уравнения $IMAGE139$ и $IMAGE47$ и некоторое множество М. Если любой корень первого уравнения, принадлежащий множеству М, удовлетворяют второму уравнению, а любой корень второго уравнения, принадлежащий множеству М, удовлетворяет первому уравнению, то эти уравнения называются равносильными на множестве М.

Пример 1. $IMAGE141$ и $IMAGE142$ не являются равносильными на множестве всех д