Индексные числа используются при описании экономических переменных. Они показывают, насколько изменилась какая либо величина за определенный промежуток времени. Например, когда говорят, что индекс прожиточного минимума составляет 120 по сравнению 1994 годом, то это означает что прожиточный минимум увеличился на 20 % за период, прошедший с 1994 года. Индексные числа также применяются для измерения динамики уровня производительности, безработицы и заработной платы.
Директор завода хотел бы сравнить затраты на производство единицы продукции с затратами которые были шесть месяцев назад.
Исследовательская группа медиков хотела бы сопоставить количество случаев заболевания гриппом в данном году с данными по предшествующему году; покупатель хочет узнать, каким ожидается рост цен на мясные продукты, чтобы соответствующим образом планировать свой бюджет и т. п. В каждом из перечисленных случаев необходимо определить степень изменения измеряемого показателя и выразить ее конкретным числом.
1. Определение простого индексного числа.
Индексное число вычисляется нахождением отношения между текущим и базовым значениями показателя. Затем, умножая полученный результат на 100, получаем процентное выражение индекса. Это окончательное значение называется относительным процентом. Заметим, что индексное число для базовой точки всегда составляет 100%.
Вычисление простого индекса. Статистическое управление располагает данными, характеризующими число вновь зарегистрированных структур бизнеса. Данные показывают, что в 1974 г. было создано 9300 новых структур, в 1984 г. - 9600 и в 1989 г. -10100. Приняв 1974 г. за базовый, можно подсчитать простой индекс, отражающий количественные изменения, как показано в табл. 1.1.[1]Проведя эти вычисления, мы приходим к выводу, что количество новых фирм в 1979 г. имеет индекс 70 относительно 1974 г. Другими словами, число новых структур бизнеса в 1979 г. составило 70% от их числа в 1974 г.
Типы индексов.
Существует три основных типа индексов: ценовой, количественный и стоимостной.
Ценовой индекс используется наиболее часто. Он применяется для сравнения уровня цен одного периода с другим. Широко известный индекс потребительских цен, предоставляемый Статистическим управлением, показывает общее изменение цен на целый ряд потребительских товаров и услуг и используется как показатель уровня жизни
Таблица 1.1
Подсчет индексных чисел (базовый год -1974)
| Год (1) | Количество новых структур*1000 (2): | Отношение (2) : 9.3 (3) | Индекс или относ процент:(3)*100 (4). |
| 1974 1979 1984 1989 | 9.3 6.5 9.6 10.1 | 9.3:9.3 = 1.00 6.5:9.3=0.70 9.6:9.3 = 1.03 10.1 :9.3 = 1.09 | 1.0 * 100 = 100 0.70*100=70 1.03 * 100 = 103 I11.09 * 100 = 109 |
Количественный индекс показывает, как переменная, отражающая число или количество, изменяется во времени. В нашем примере был вычислен именно количественный индекс, определяющий соотношение между данными за 1979 г., 1984г., 1989 г. и данными за базовый 1974 г.
Часто индекс характеризует изменение переменной во времени, как и в случае временных рядов. В то же время, его можно использовать и для оценки изменения показателей в зависимости от места сбора информации. Это достигается одновременным сбором данных в различных местах с их последующим сравнением. Например, сравнительный индекс прожиточного минимума показывает, что, исходя из стоимости основных товаров и услуг, дешевле жить в Остине (штат Техас), чем в Нью-Йорке.
Стоимостной индекс характеризует изменения в общей стоимости денежных средств. Таким образом, он определяет изменения в стоимости доллара как переменной. При подсчете стоимостного индекса учитывают ценовые и количественные изменения для получения наиболее полной информации. В нашем примере- был определен лишь количественный индекс. Однако мы могли бы рассмотреть и долларовый эффект при помощи подсчета общей капитализированной стоимости для рассматриваемых лет. В (табл1.2) представлены соответствующие стоимостные индексы для 1979, 1984 и 1989 гг. Согласно этим расчетам, стоимостной индекс предприятий в 1989 г. был равен 160.
Таблица 1.2
Подсчет стоимостного индекса (1974 г. - базовый)
| Год (1) | Общая стоимость (млн. долл.) (2) | Отношение (2): 18.4 (З) | Индекс (3) * 100 (4) |
| 1974 1979 1984 1989 | 18.4 14.6 26.2 29.4 | 18.4:18.4 = 1.00 14.6:18.4=0.79 26.2:18.4 = 1.42 29.4 :18.4 = 1.60 | 1.00* 100 = 100 0.79*100= 79 1.60* 100 = 142 1.60 * 100 = 160 |
Сводный индекс характеризует свойства группы изменяющихся переменных. Индекс потребительских цен определяет общий уровень цен на определенные товары и услуги, объединяя индивидуальные цены на товары и услуги в одном значении сводного ценового индекса.
Наиболее часто индексные числа применяются в качестве конкретного конечного результата. Такие показатели, как индекс потребительских цен. часто встречаются в прессе как общие оценки состояния экономики.
Менеджеры используют индексы как часть промежуточных расчетов. В табл. 1.3 показана еженедельная зарплата секретаря за несколько лет, соответствующий потребительский ценовой индекс и подсчет реальной зарплаты секретаря. Номинальная зарплата секретаря заметно увеличилась, но ее реальная покупательная способность росла не столь быстрыми темпами. Это можно объяснить одновременным ростом индекса прожиточного минимума со 100 до 200 единиц.
Таблица 1.3
Подсчет реальной заработной платы
| Год (1) | Недельная зарплата (долл.) (2) | Потребит. ценовой индекс (3) | (2) * 100/ (3) (4) | Реальная зарплата, (долл.) (5) |
| 1973 1979 1989 | 114.75 145.50 472.98 | 100 123 200 | 114.75 * 100:100 145.50 * 100:123 472.98*100:200 | 114.75 118.29 236.44 |
Проблемы, связанные с индексными числами.
Искажения, возникающие при использовании индексных чисел, могут быть вызваны следующими факторами:
1. Ограниченность данных. Иногда довольно трудно найти подходящие данные для вычисления индекса. Например, коммерческий директор небольшой авиастроительной компании хотел бы подсчитать индекс, характеризующий сезонные различия в объеме продаж небольших самолетов. Если он располагает данными только по годовому объему продаж, то определить сезонные колебания будет невозможно.
2. Несравнимость индексов. Часто пытаются сравнивать один индекс с другим после того, как в технологии производства или в общей экономической ситуации произошли радикальные изменения. Если сравнивать цены на автомобили в 1979 г. и в 1989 г., то выяснится, что цены в значительной степени выросли. Однако, это сравнение не учитывает технологического прогресса в автомобилестроении за эти 10 лет.
3. Неправильно выбранный вес так же могут привести к искажениям индекса. В процессе подсчета сводного индекса необходимо учитывать, что изменения одних переменных могут быть важнее, чем изменения других. Влияние на экономику 50-ти центового увеличения в цене за один галлон бензина не может быть компенсировано уменьшением цен на автомобили на те же 50 центов. Очевидно, что увеличение цены одного галлона на 50 центов имеет гораздо большее влияние на потребителя. Следовательно, большой вес должен быть присвоен возросшей цене на горючее, чем снижению цен на автомобили.
4. Искажение индекса может являться результатом неправильно выбранной базы. Иногда фирма выбирает такую базу, которая автоматически приводит к результату, отражающему интерес самой фирмы. Предположим, что общество по борьбе с чрезмерным расходом нефти хочет выставить нефтеперерабатывающие компании в плохом свете. Оно может измерять доходы текущего года, приняв в качестве базы какой-либо убыточный год. Тогда, несомненно, индекс отразит значительное увеличение доходов компании. С другой стороны, общество, выступающее за неограниченное потребление нефти, хотело бы показать, что в текущем году доходы от продажи нефти были минимальными. Тогда для базы можно выбрать год с весьма высокой прибылью. В результате, индекс покажет незначительное увеличение или даже сокращение доходов от продажи нефти. Следовательно, особое внимание должно уделяться тому, как и почему был выбран данный базовый период, и лишь затем делать выводы на основе сравнения индексных чисел.
2. Невзвешенный агрегативный (совокупный) индекс.
Самой простой формой сводного составного индекса является невзвешенный агрегативный индекс. Невзвешенный означает, что все значения, рассматриваемые в процессе подсчета индекса, входят с одинаковым весом. Агрегативный (совокупный) означает, что мы суммируем все значения. Главное преимущество этого индекса - его простота.
Подсчет невзвешенного совокупного индекса. Невзвешенный совокупный индекс вычисляется сложением всех элементов для данного временного периода с последующим делением результата на сумму этих же элементов для базового периода. Формула для подсчета невзвешенного совокупного индекса (НСИ):
НСИ=  *100 (2.1) где
*100 (2.1) где
P0- количество каждого элемента для базового года;
P1 - количество каждого элемента для текущего года.
Заметим, что в качестве P0 и P1 мы можем подставлять в эту формулу цены или стоимости для нахождения соответственно ценового или стоимостного индексов. Хотя индексы и выражены в виде процента, обычно используются только их значения и опускается знак процента при обработке индексных чисел.
Применение невзвешенного индекса.
В табл.2.4 показано вычисление этого индекса. В данном примере мы определяем изменения в общем уровне цен на основе изменений цен на несколько наименований товаров. Цены 1984 г. являются базовыми значениями, которые сравниваются с ценами 1989г.
Таблица 2.4
Подсчет невзвешенного индекса
| Элементы совокупного | Цены ( долл.) |
| индекса | 1984 г (P0) | 1989 г. (P1) |
| Молоко (1 галлон) Яйца (1 дюжина) Гамбургер (1 фунт) Бензин (1 галлон) | 1.92 0.81 1.49 1.00 | 3.40 1.00 2.00 1.17 |
| | SP0=5.22 | SP1=7.57 |
Невзвешенный совокупный индекс = 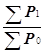 *100=
*100= 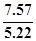 *100=145
*100=145
Интерпретация индекса.
Используя данный расчет, мы определяем, что цено